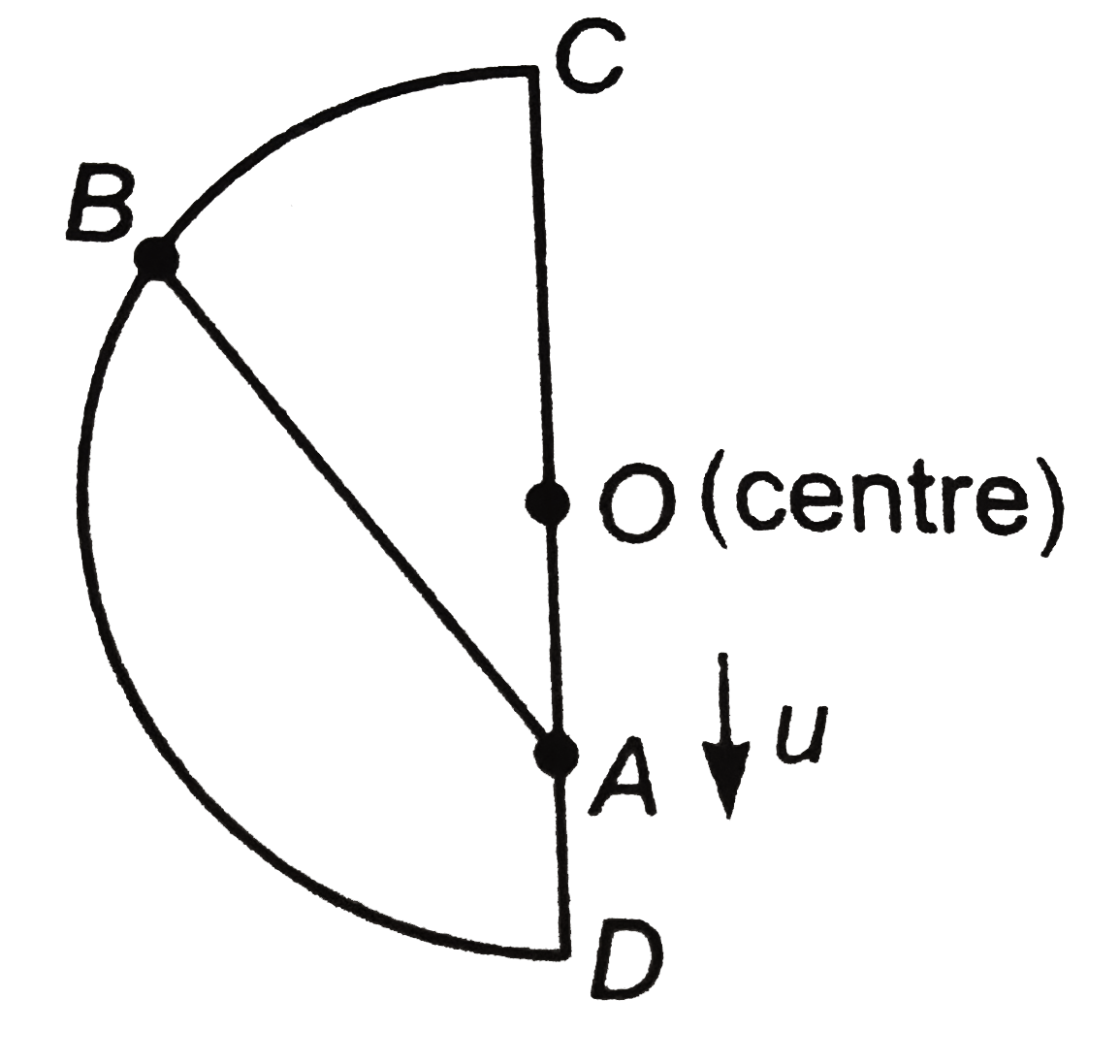
Two block A and Bmove along a semicircular wire frame as shown in figure. The beads are connected by an inelastic string wich always remains tight . At an instant the speed of A is u,∠BAC=45∘andBOC=75∘,where O is the center of the semicircular are. The speed of bead B at that instant is
√2u
u
u2√2
√23u
The correct Answer is:A
Distance AB= constant
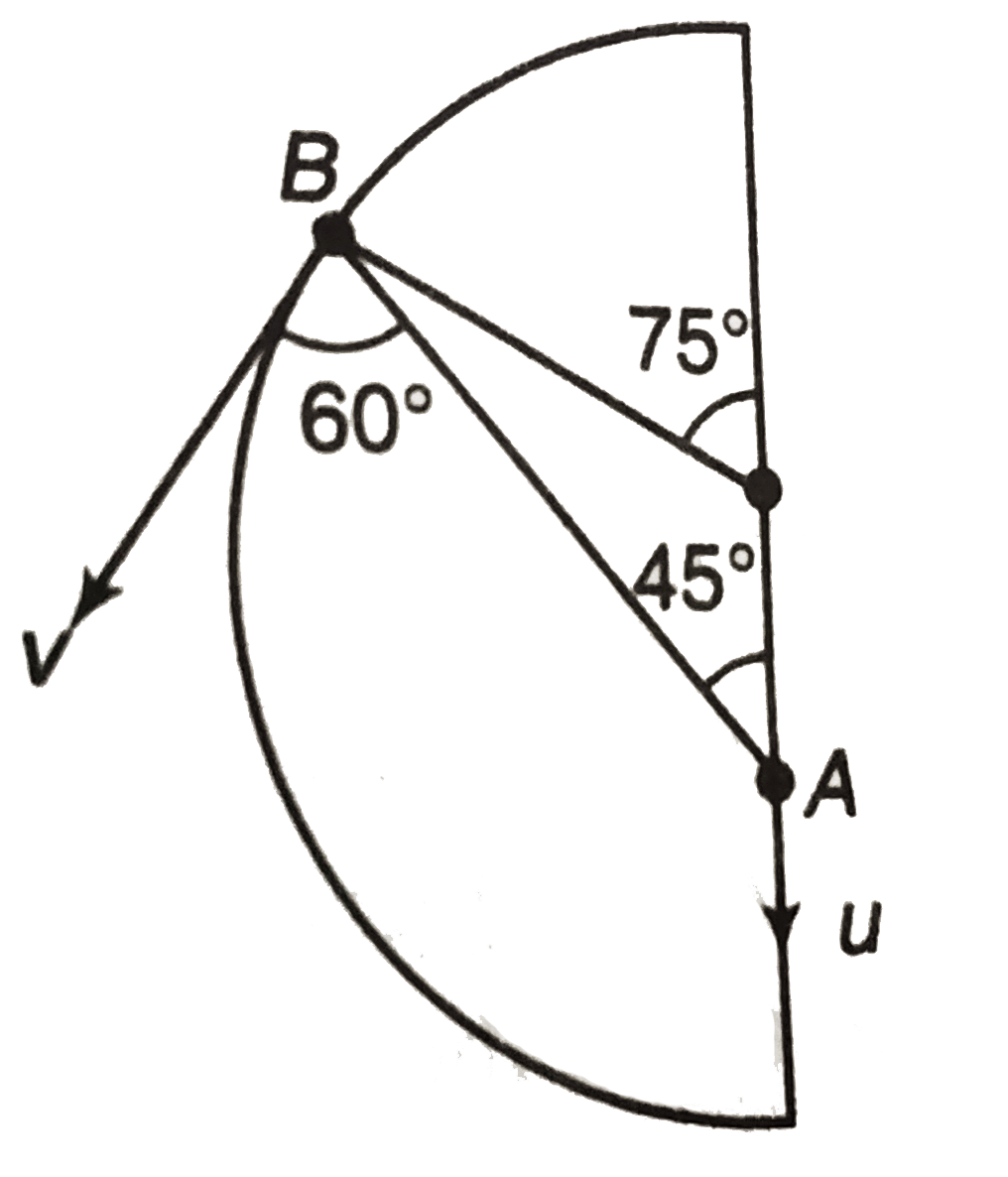
∴ Component of ν along BA= component of u along BA
or νcos60∘=ucos45∘
or ν=√2u
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct
90 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Two beads A and B move along a semicircular wire frame as shown in figure. The beads are connected by an inelastic string which always remains tight . At an instant the speed of A is u,∠BAC=45∘andBOC=75∘,where O is the centre of the semicircular arc. The speed of bead B at that instant is

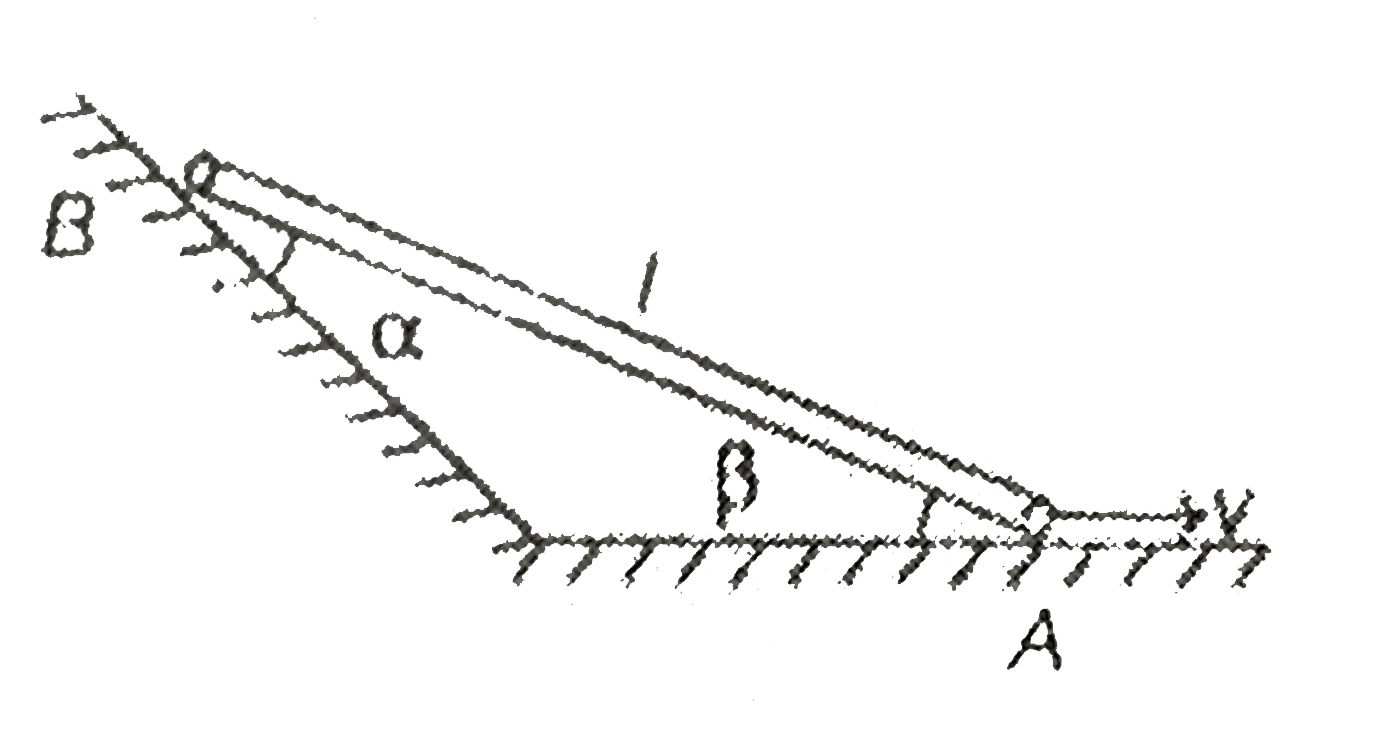
View SolutionA rod of length l slided down along the inclined wall as shown in figure. At the instant shown in figure, the speed of end A is v, then the speed of B will be
View Solution
Knowledge Check
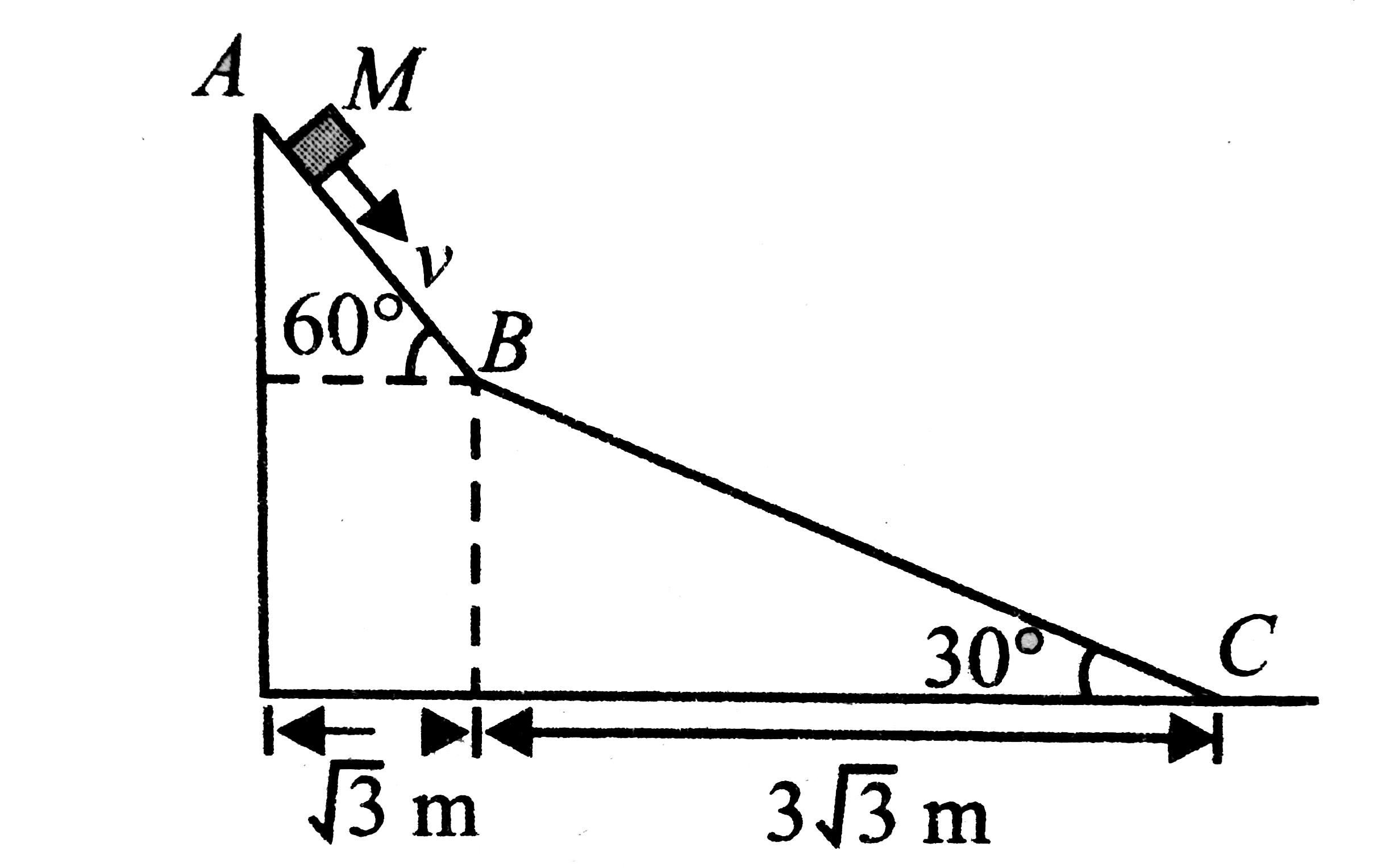
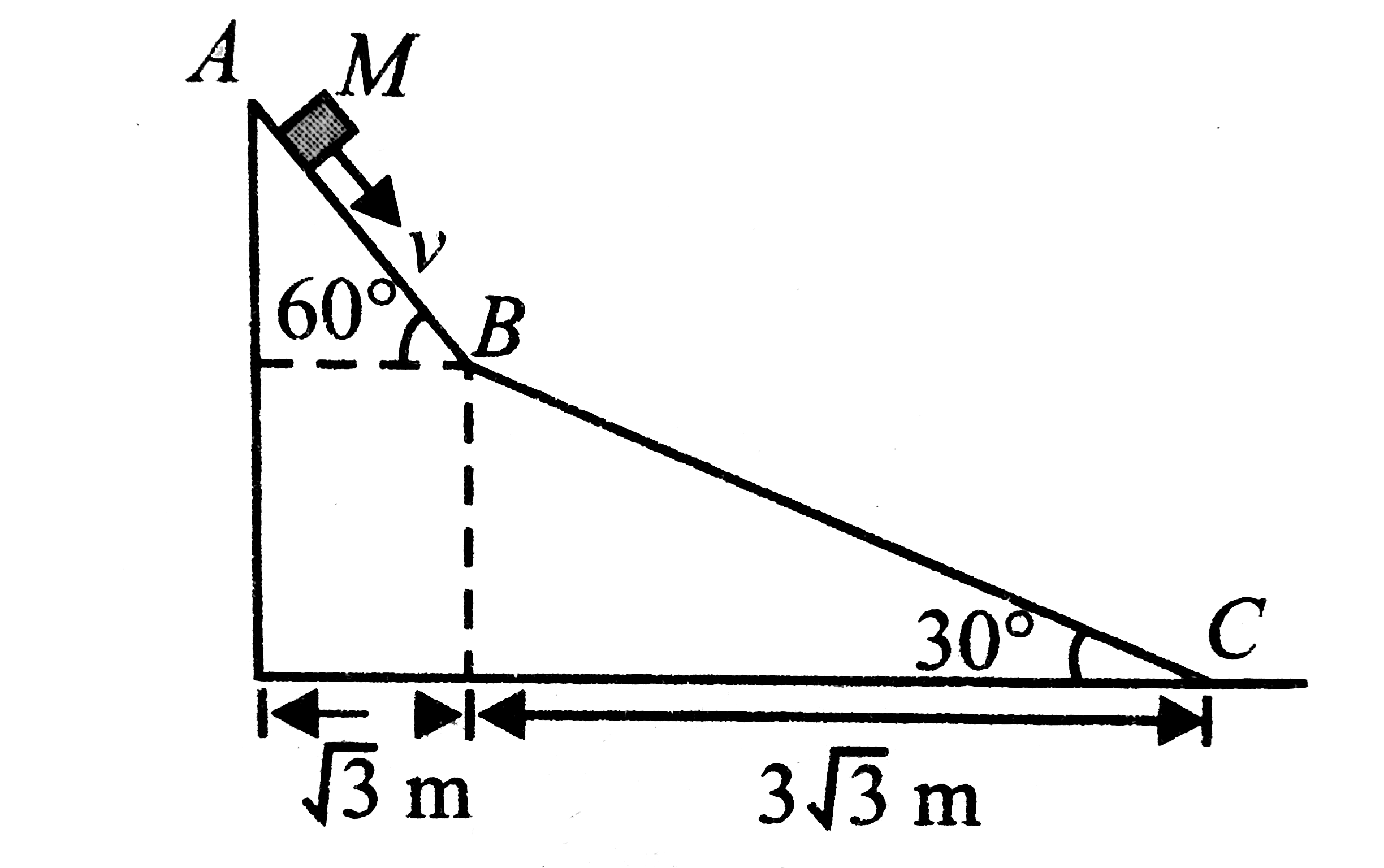
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point B immediately after it strikes the second incline is
 A√60 m/sB√45 m/sC√30 m/sD√15 m/s
A√60 m/sB√45 m/sC√30 m/sD√15 m/s

A rod AB is moving on a fixed circle of radius R with constant velocity v as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distancex=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
(i) Find the speed of point of intersection P.
(b) Find the angular speed of point of intersection P with respect to centre of the circle.
View SolutionA rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
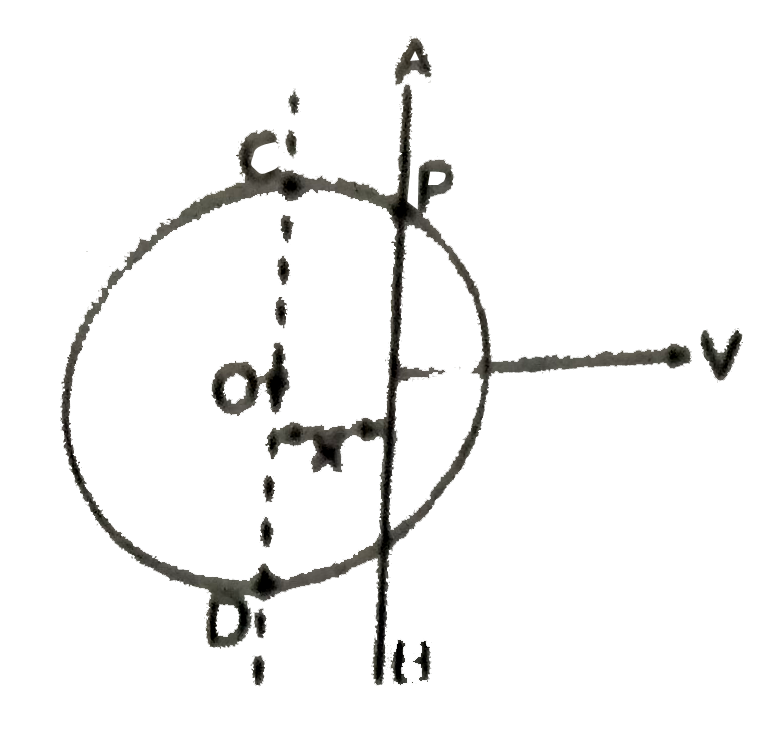
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
View SolutionTwo blocks are connected over a massless pulley as shown in figure. The mass of block A is 10 kg and the coefficient of kinetic friction is 0.2 Block A sliders down the incline at constant speed. The mass of block B in kg is

View SolutionTwo blocks of masses 2m and m are in equilibrium a shown in the figure. Now the string between the blocks is suddenly broken. The accelarations of the blocks A and B respectively, at that instant are

View SolutionTwo identical blocks A and B are connected with a spring of constant k as shown in ligure. If block B s moving rightward with speed V0 maximum extension of spring is
View SolutionA small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point C, immediately before it leaves the second incline
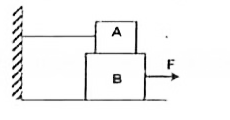
View SolutionTwo blocks A and B having masses 100 kg and 200 kg are placed as shown in the figure. The block A is connected to a wall with a light inextensible string. The coefficient of friction between the blocks is 0.3 and that between the block B and the floor is 0.03. Then the minimum force required to move the block B will be (take g=10m/s2)
View Solution
