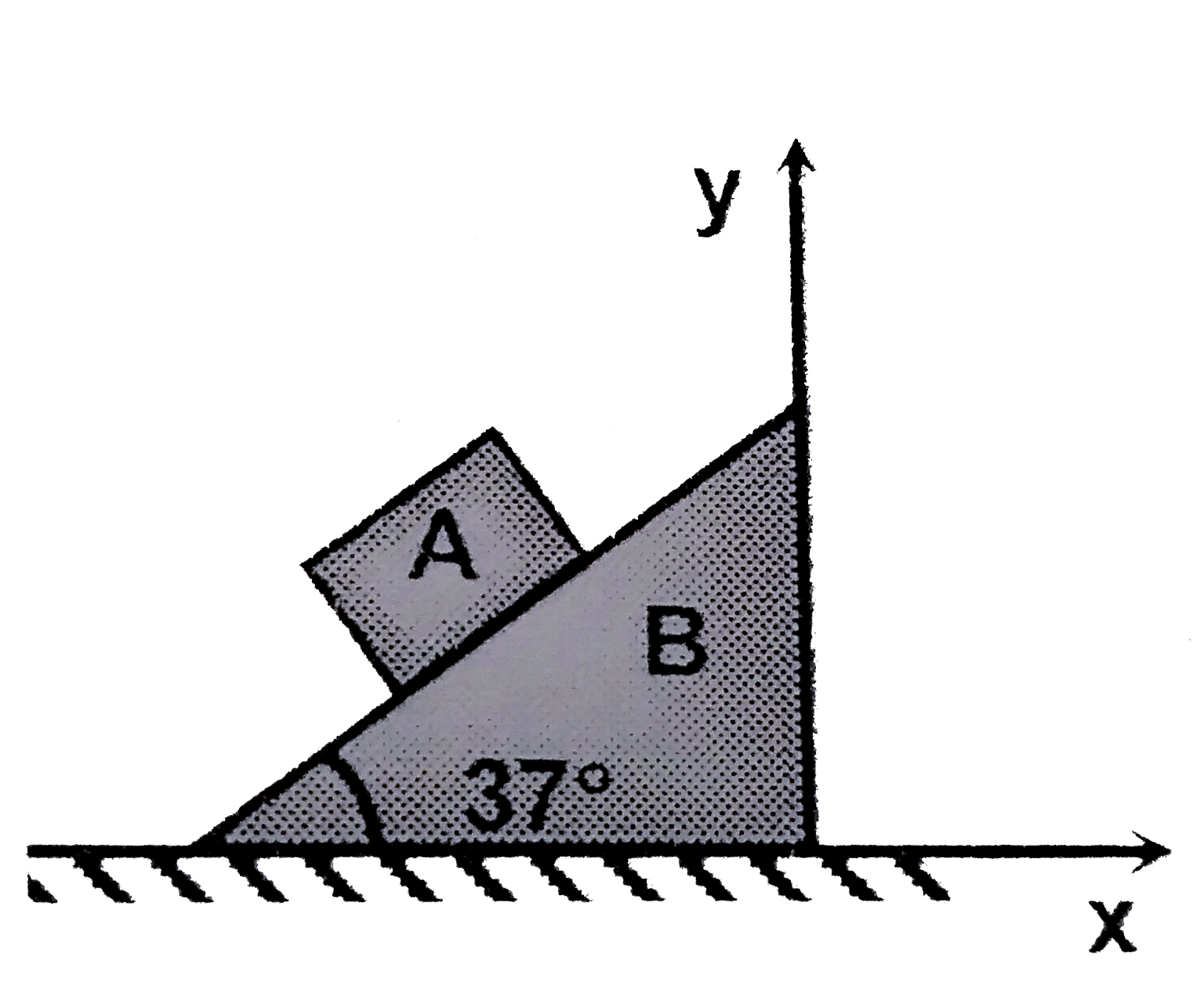
In the figure shown the accelerationof A is aA=(15ˆi+15ˆj). Then the acceleration of B is (A remain in contact with B)
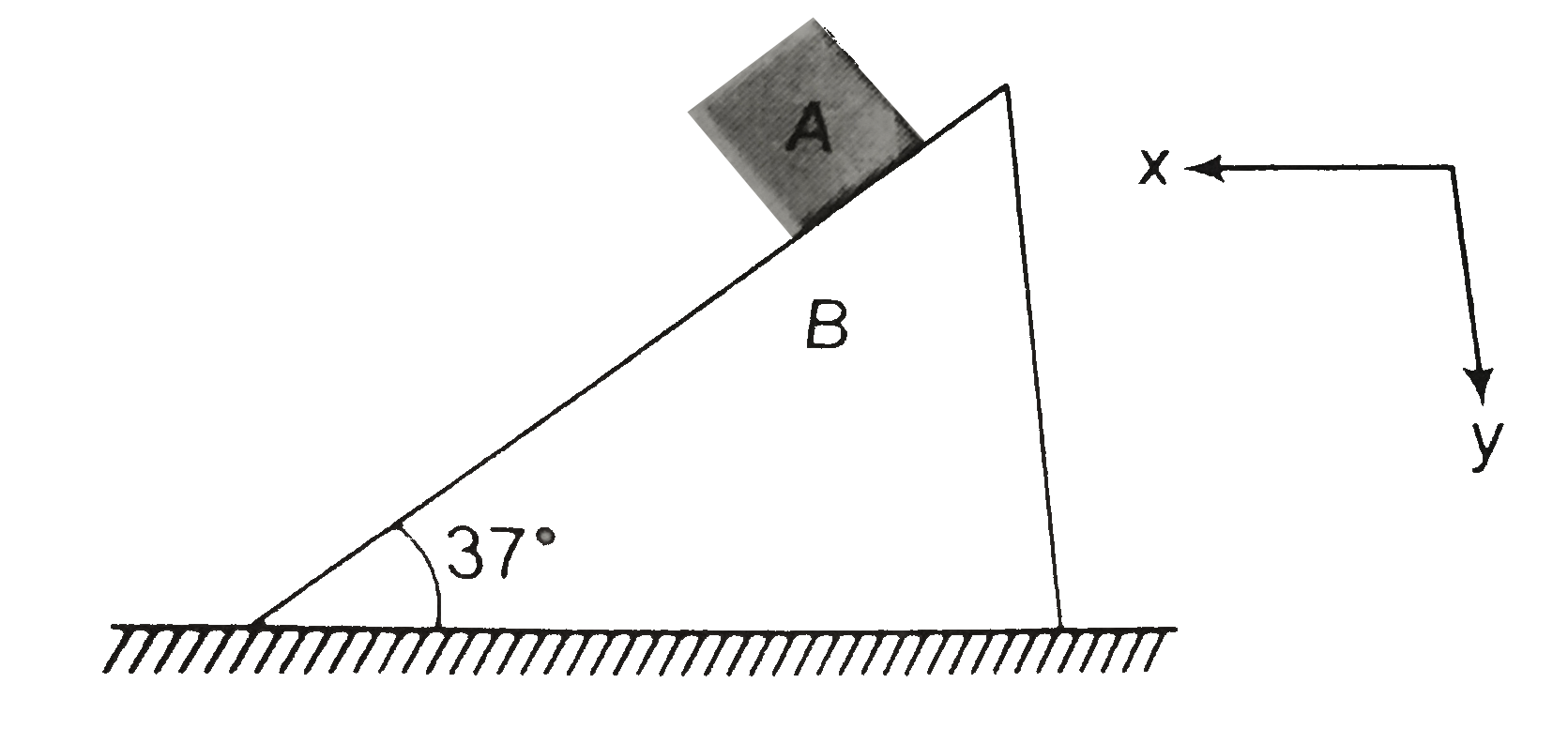
5ˆi
−15ˆi
−10ˆi
−5ˆi
The correct Answer is:D
Let aB=aˆi
Then, aAB=aA−aB
=(15−a)ˆi+15ˆj

Since aAB is along the plane as shown in figure.
∴tan37∘=34=1515−a
Solving this equation , we get a=−5
or aB=(−5ˆi)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct
90 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
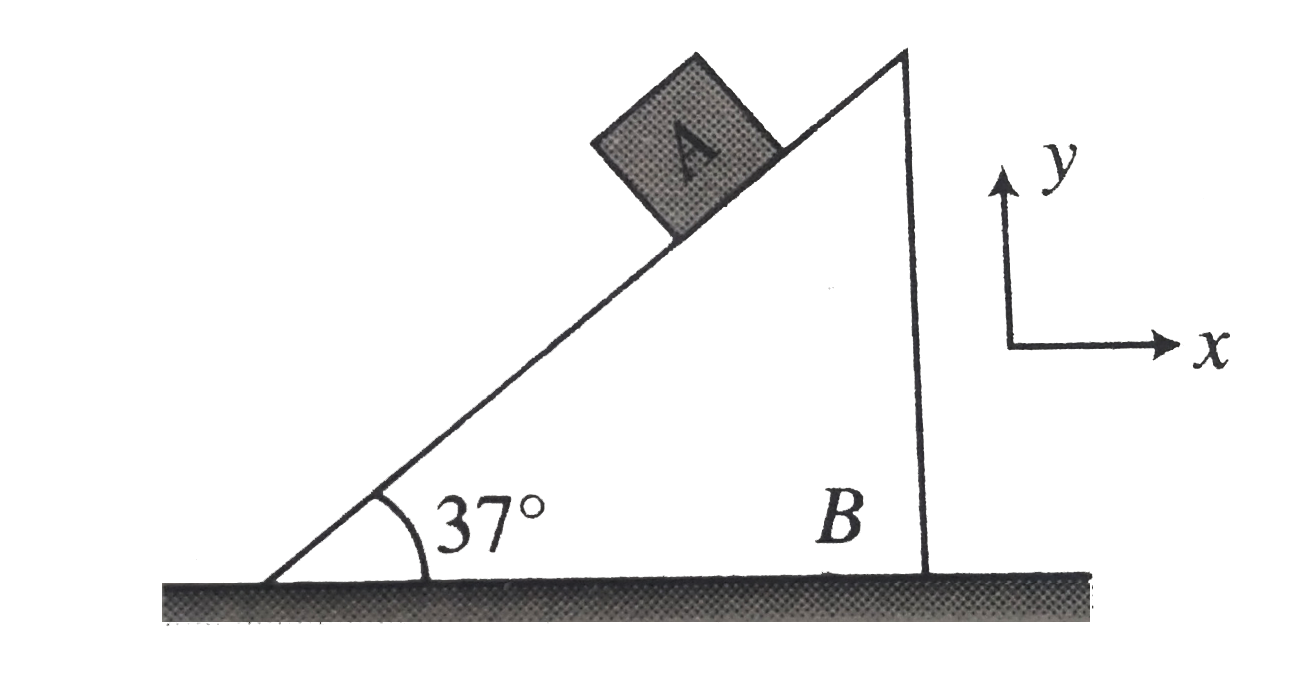
In fig, the acceleration of A is →aA=15ˆi+15ˆj. Then the acceleration of B is (A remains in constact with B)
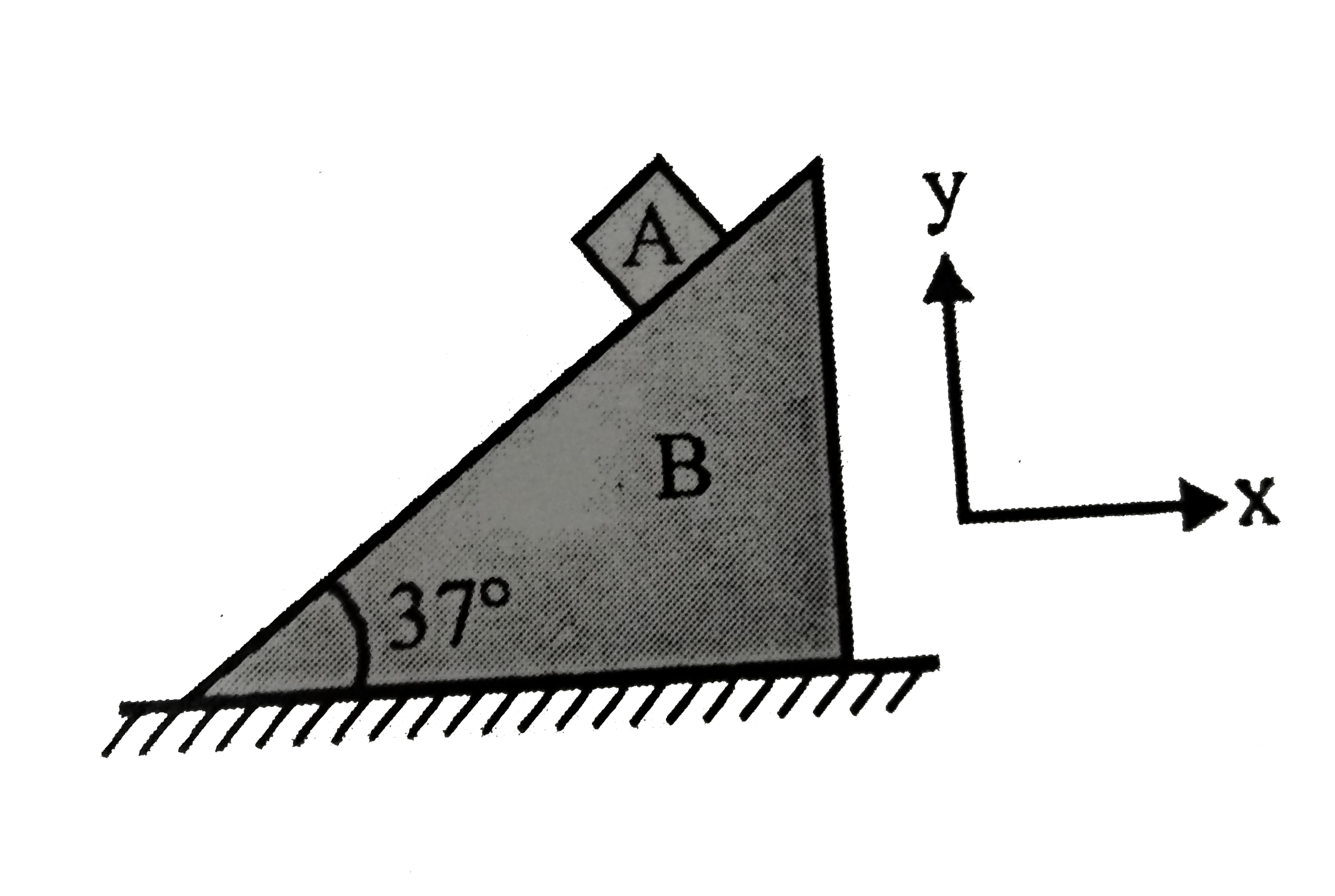
View SolutionIn the figure shown the acceleration of A is, ¯aA=(15ˆi+15ˆj)m/s2. If A is sliding on B then the acceleration of B is.
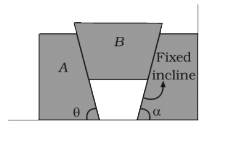
View SolutionIn the situation as shown in the figure if acceleration of B is a, then find the acceleration of A (B always remain horizintal),

View SolutionIn the arrangement shown in figure, if the acceleration of B is ¯a , then find the acceleration of A
View SolutionIn the figure shown find relation between magnitudes of aA and aB.

View SolutionIn the figure shown find relation between magnitudes of aA and aB.

View SolutionIn the figure shown neglecting friction and mass of pulley, what is the acceleration of mass B ?
View SolutionIn the figure shown the velocity of A with respect to ground is (20ˆi+15ˆj)m/s, then what will be the magnitude of velocity of the wedge 'B' with respect to ground frame. (A remains in contact with B)
View SolutionA particle starts from origin at t=0 with a velocity of 15ˆims−1 and moves in xy-plane under the action of a force which produces a constant acceleration of 15ˆi+20ˆjms−2. Find the y-coordinate of the particle at the instant its x-coordinate is 180 m.
View SolutionThe projection of ¯¯¯A=2ˆi+2ˆj+5ˆk on to ¯¯¯B=ˆi−ˆj is:
View Solution
