A block of mass m is welded with a light spring of stiffness k. The spring is initially relaxed. When the wedge fitted moves with an acceleration a, as shown in figure. $8.60$ , the block slides through a maximum distance $l$ relative to the wedge. If the coefficient of kinetic friction between the block and the wedges is $μ$ , find the maximum deformation $l$ of the spirng by using work-energy theorem.

Video Solution

Text Solution

Verified by Experts

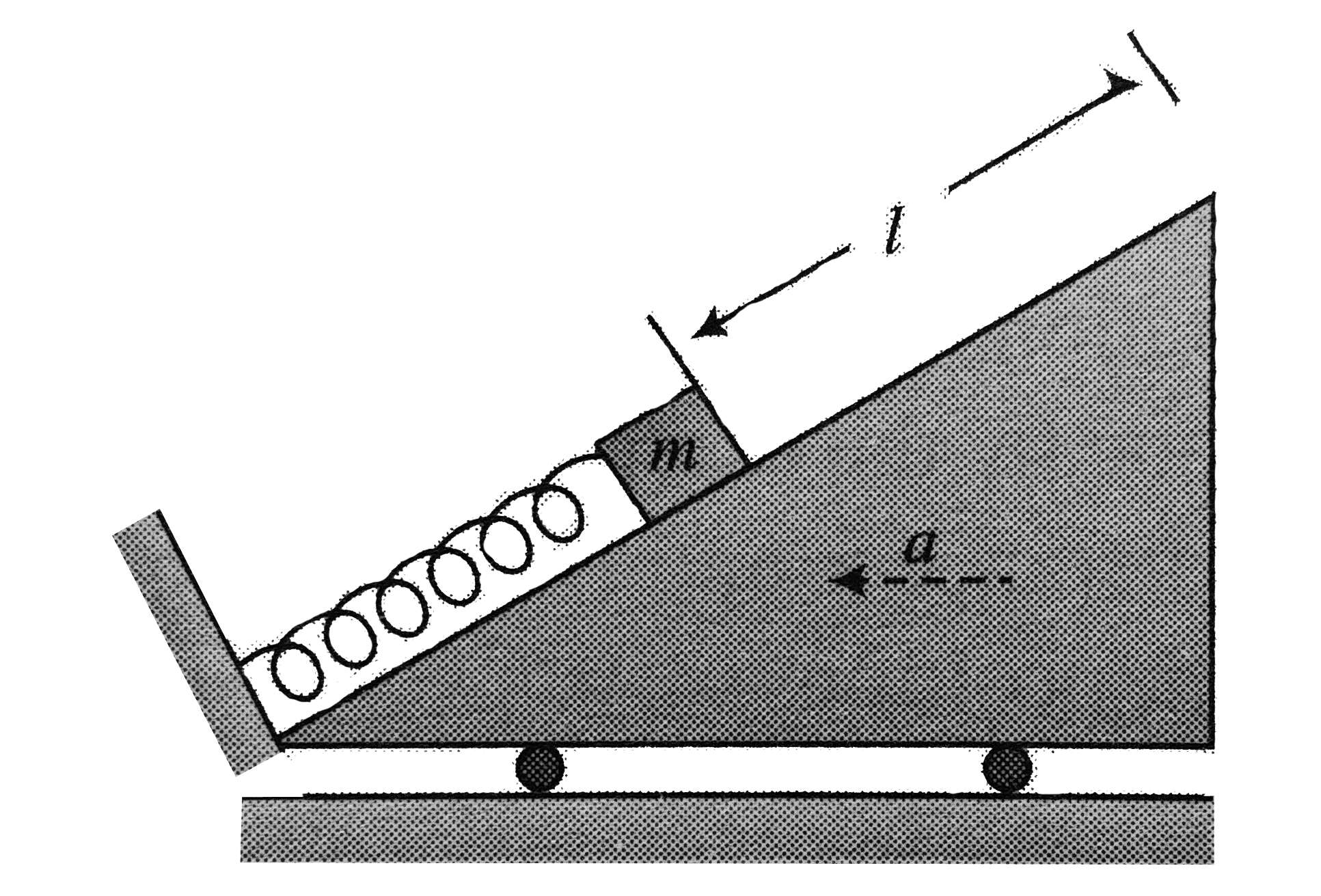
In this case, we are given the block slides through a distance $l$ relative to the wedge. We can apply work-energy theorem from the frame of reference of wedge.

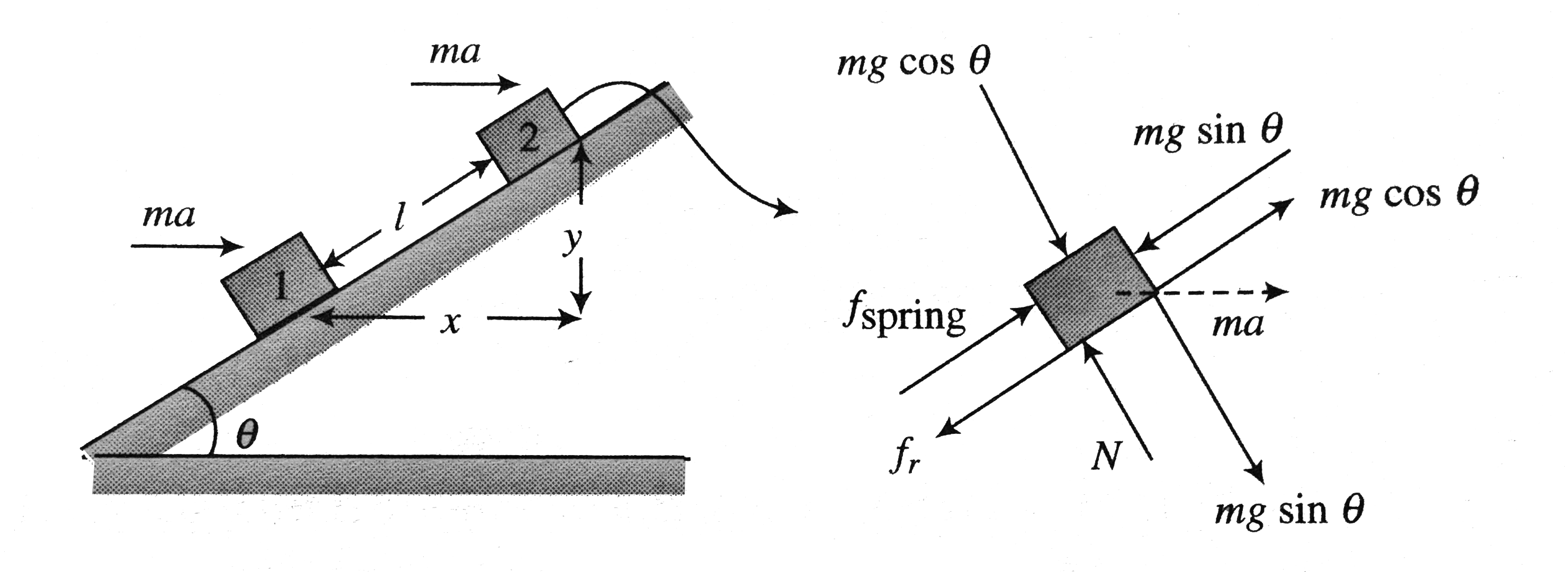
While the block is displaced from point 1 to point 2, work done by all the forces are given as follows:
Work: $W_{g r} = - m g l sin θ$ , $W_{s p} = \frac{- K l^{2}}{2}$
$W_{f} = (μ N) \cdot l$
$N = m g cos θ + m a sin θ$
$W_{f} = - μ m g l cos θ - μ m a sin θ$
and $W_{p s e u d o} = (m a cos θ) l = m a l cos θ$
W-E theorem: Summing upall workds, the total done is
$W_{t o t a l} = W_{g r} + W_{s p} + W_{f} + W_{p s e u d o}$
$W = - \frac{m g l sin θ}{1} - \frac{μ m g l cos θ}{3} + \frac{m a l cos θ}{4} - \frac{\frac{1}{2} k l^{2}}{2} + F l - \frac{μ m a l sin θ}{3}$
Since the block was at rest at 1 and will remain at rest relative to the wedge, we can write $Δ K = 0$ (relative to the wedge). Using work-energy theorem relative to the wedge, we have $W = Δ K = 0$ .
Substituting $W = 0$ , we have
$- m g / sin θ - \frac{1}{2} k l^{2} - μ m g cos θ - μ m a l sin θ + m a l cos θ = 0$
$l = \frac{2}{k} [m a (cos θ - μ sin θ) - m g (sin θ + μ cos θ)]$
$= \frac{2 m}{k} [a (cos θ - μ sin θ) - g (sin θ + μ cos θ)]$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-WORK, POWER & ENERGY-Archives (integer)

Home
Ask Doubt
Profile