The minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
g(cosθ+μsinθsinθ−μcosθ)
g(sinθ+μcosθcosθ−μsinθ)
g(sinθ−μcosθsinθ+μcosθ)
g(cosθ−μsinθsinθ+μcosθ)
The correct Answer is:B
To solve the problem of finding the minimum value of acceleration of the wedge for which the block starts sliding on the wedge, we can follow these steps:
Step 1: Understand the System
We have a wedge inclined at an angle θ with a block resting on it. The wedge is accelerating horizontally, and we need to determine the minimum acceleration a of the wedge that will cause the block to start sliding down.
Step 2: Draw the Free Body Diagram (FBD)
Draw the FBD of the block on the wedge. The forces acting on the block are:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the surface of the wedge.
- The frictional force f acting parallel to the surface of the wedge, opposing the motion.
Step 3: Resolve Forces
Resolve the gravitational force mg into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
Step 4: Apply Newton's Second Law
For the block to start sliding down, the net force acting on it along the incline must overcome the frictional force. The frictional force can be expressed as:
f=μN
where μ is the coefficient of friction.
The equations of motion can be set up as follows:
1. In the direction perpendicular to the incline:
N=mgcosθ−masinθ
2. In the direction parallel to the incline:
macosθ=mgsinθ+f
Step 5: Substitute the Frictional Force
Substituting the expression for the frictional force f:
macosθ=mgsinθ+μ(mgcosθ−masinθ)
Step 6: Rearranging the Equation
Rearranging the equation gives:
macosθ+μmasinθ=mgsinθ+μmgcosθ
Factoring out ma on the left side:
ma(cosθ+μsinθ)=mg(sinθ+μcosθ)
Step 7: Solve for Acceleration a
Now, we can solve for a:
a=g(sinθ+μcosθ)cosθ+μsinθ
Conclusion
Thus, the minimum value of acceleration a of the wedge for which the block starts sliding is:
a=g(sinθ+μcosθ)cosθ+μsinθ
---
We have a wedge inclined at an angle θ with a block resting on it. The wedge is accelerating horizontally, and we need to determine the minimum acceleration a of the wedge that will cause the block to start sliding down.
Draw the FBD of the block on the wedge. The forces acting on the block are:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the surface of the wedge.
- The frictional force f acting parallel to the surface of the wedge, opposing the motion.
Resolve the gravitational force mg into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
For the block to start sliding down, the net force acting on it along the incline must overcome the frictional force. The frictional force can be expressed as:
f=μN
where μ is the coefficient of friction.
1. In the direction perpendicular to the incline:
N=mgcosθ−masinθ
2. In the direction parallel to the incline:
macosθ=mgsinθ+f
Substituting the expression for the frictional force f:
macosθ=mgsinθ+μ(mgcosθ−masinθ)
Rearranging the equation gives:
macosθ+μmasinθ=mgsinθ+μmgcosθ
Factoring out ma on the left side:
ma(cosθ+μsinθ)=mg(sinθ+μcosθ)
Now, we can solve for a:
a=g(sinθ+μcosθ)cosθ+μsinθ
Thus, the minimum value of acceleration a of the wedge for which the block starts sliding is:
a=g(sinθ+μcosθ)cosθ+μsinθ
Similar Questions
A block of mass m is placed over the wedge as shown in figue Coefficent of frition μ is half the minimum value required to keep it in this postion.

what is the minimum value of accleration of wedge to keep the blok statinary with respect to the wedge in either of the four cases?

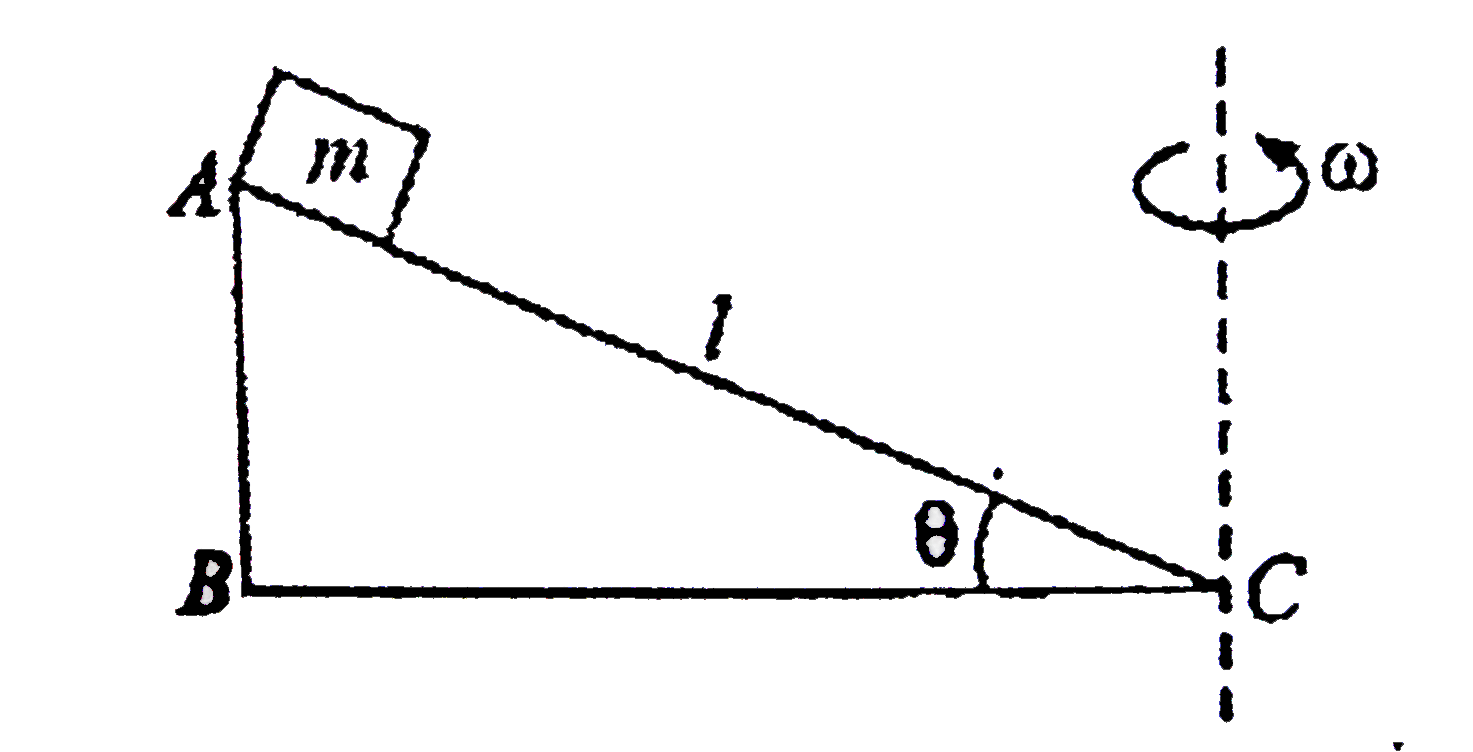
View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
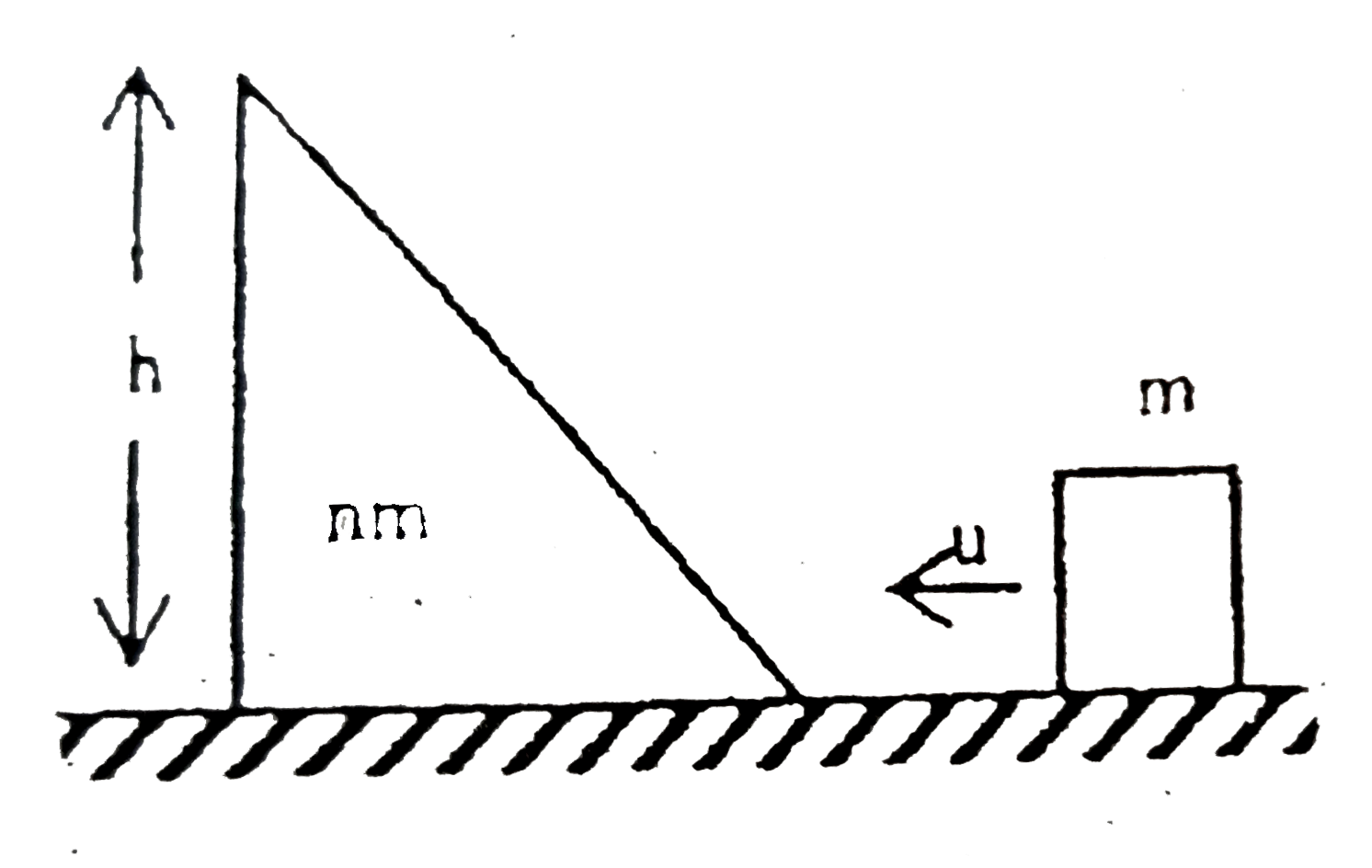
View SolutionA block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is
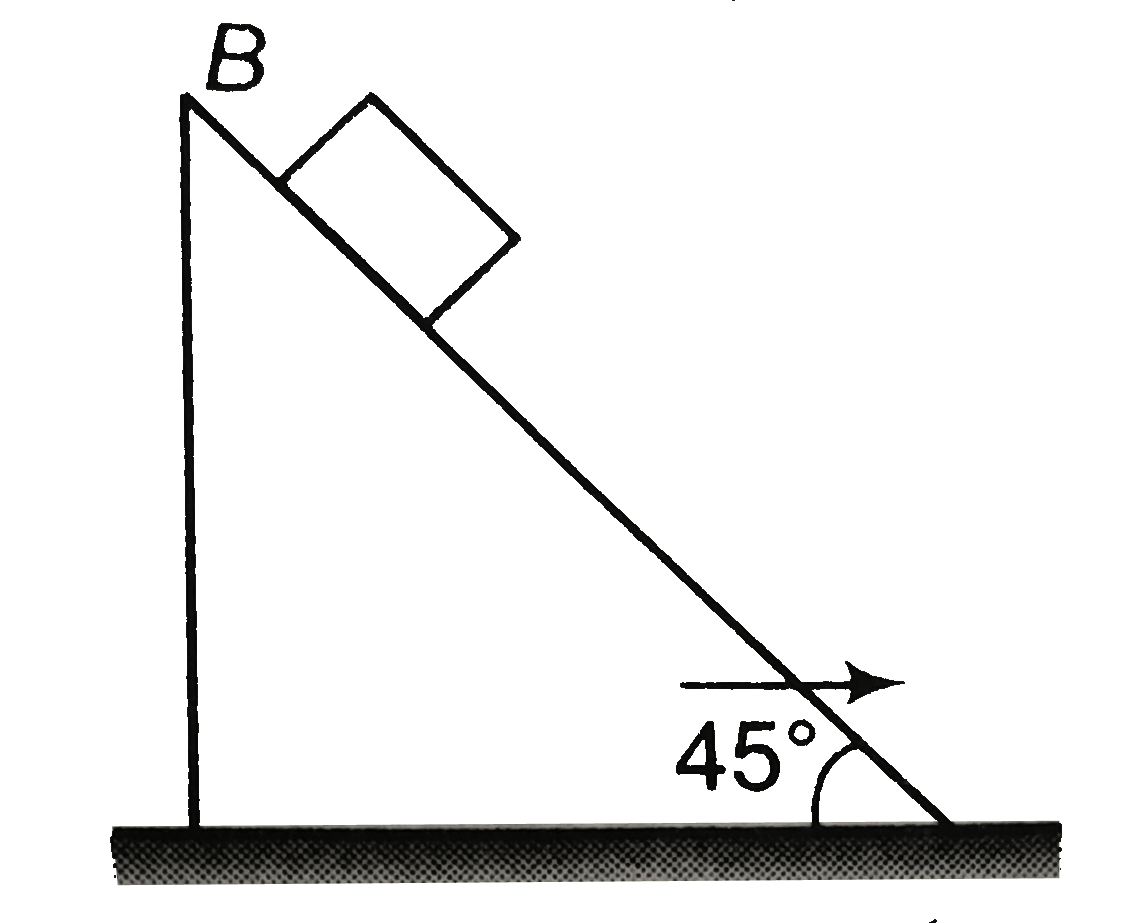
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

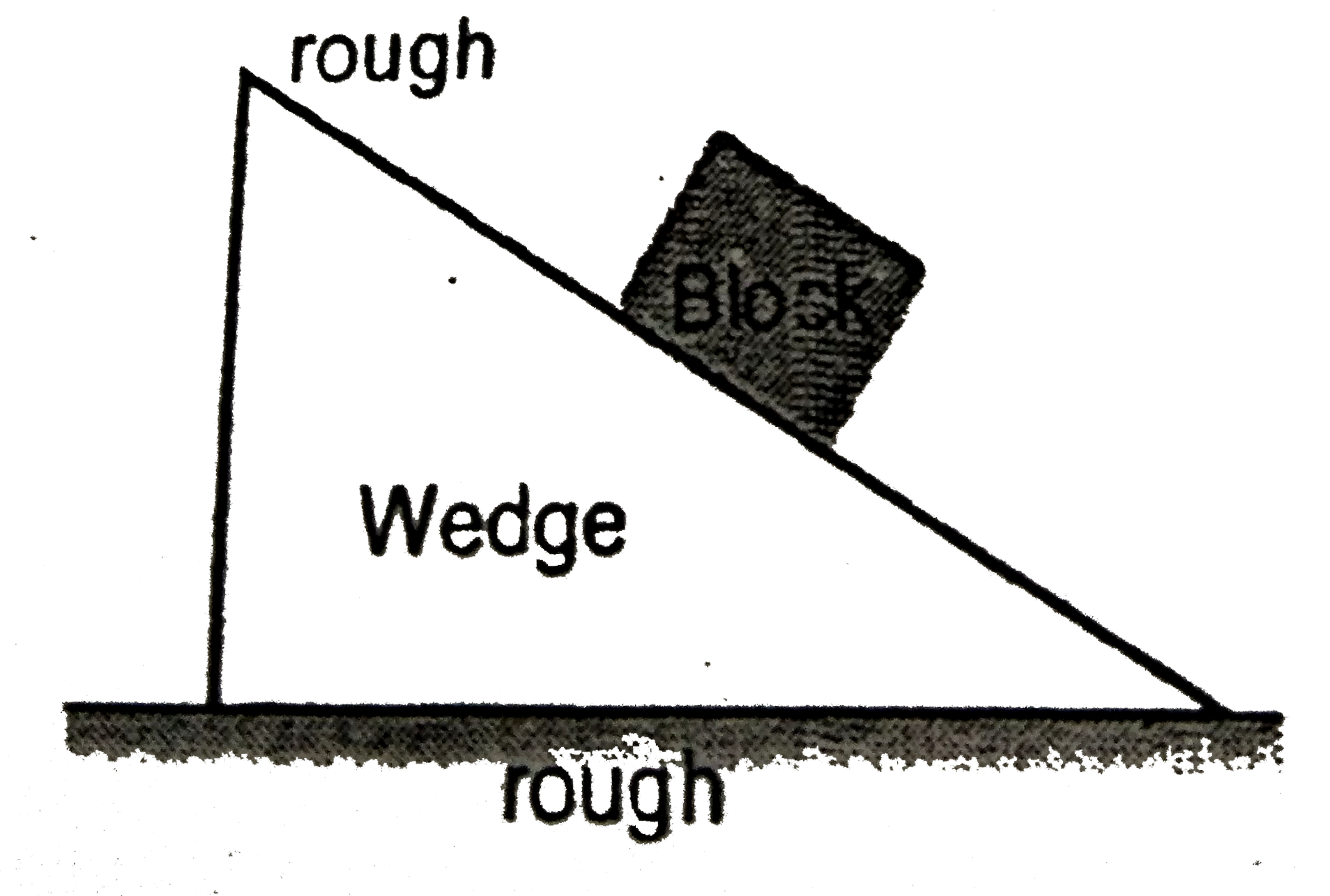
View SolutionWhen a block is placed on a wedge as shown in figure, the block starts sliding down and the wedge also start sliding on ground. All surfaces are rough. The centre of mass of ( wedge + block ) system will move.
View SolutionA small wedge whose base is horizontal is fixed to a vertical rod as shown in fig . The sloping side of the weidgeis frictionless and the wedge is span with a constant angular speed ω about vertical axis as shown in the fig find the
a. value of angular speed ω for which the block of mass m just does not slide down the wedge.
b. normal reaction on the block by wedge when block does not slip relative to wedge.

View SolutionA block of mass m is placed on a wedge The wedge can be accelerated in four manners marked as (1),(2),(3) and (4) as shown. If the normal reactions in situation (1),(2),(3) and (4) are N1,N2,N3 and N4 respectively and acceleration with which the block slides on the wedge in situation are b1,b2,b3 and b4 respectively then

View SolutionA block of mass m is placed on a wedge The wedge can be accelerated in four manners marked as (1),(2),(3) and (4) as shown. If the normal reactions in situation (1),(2),(3) and (4) are N1,N2,N3 and N4 respectively and acceleration with which the block slides on the wedge in situation are b1,b2,b3 and b4 respectively then

View SolutionA block of mass m is placed on a smooth wedge of inclination Q. The whole system is accelerated horizontally so that the block does not slip on the wedge. Find the
i) Acceleration of the wedge
ii) Force to be applied on the wedge
iii) Force exerted by the wedge on the block.
View Solution
