A river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river. 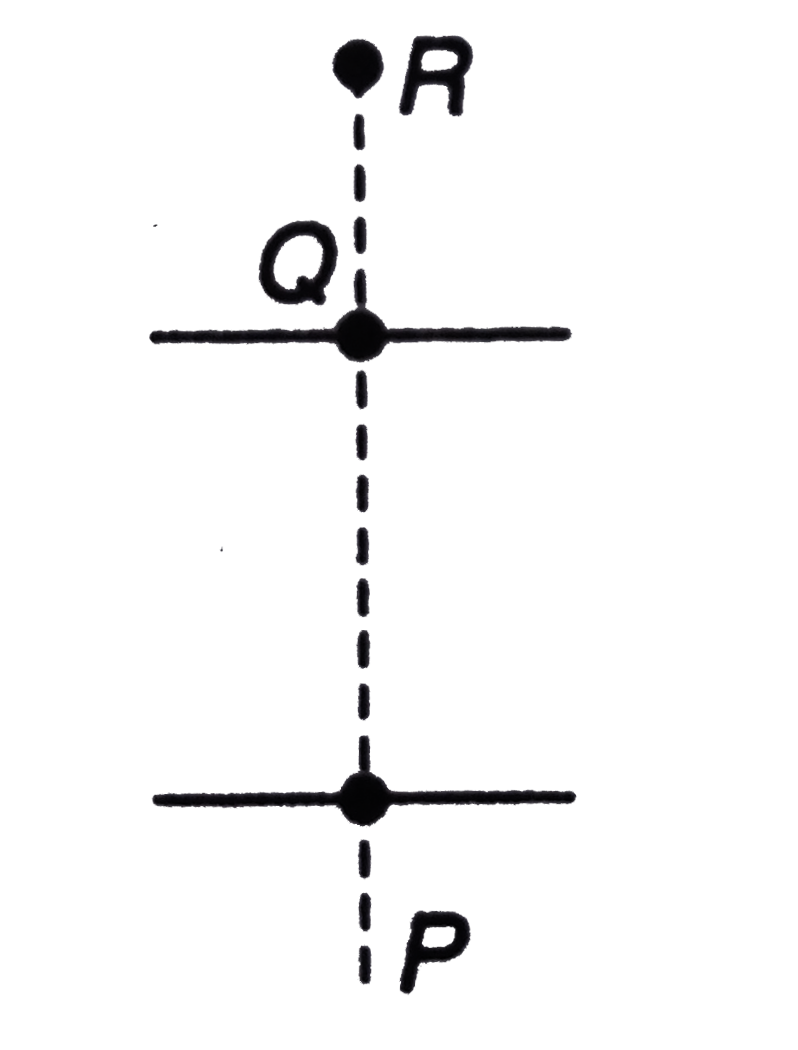
The correct Answer is:A, B, C
(a) Since, the resultant velocity is always
perpendicular to the line joining boat and R, the boat
is moving in a circle of radius 2ω and centre at R.
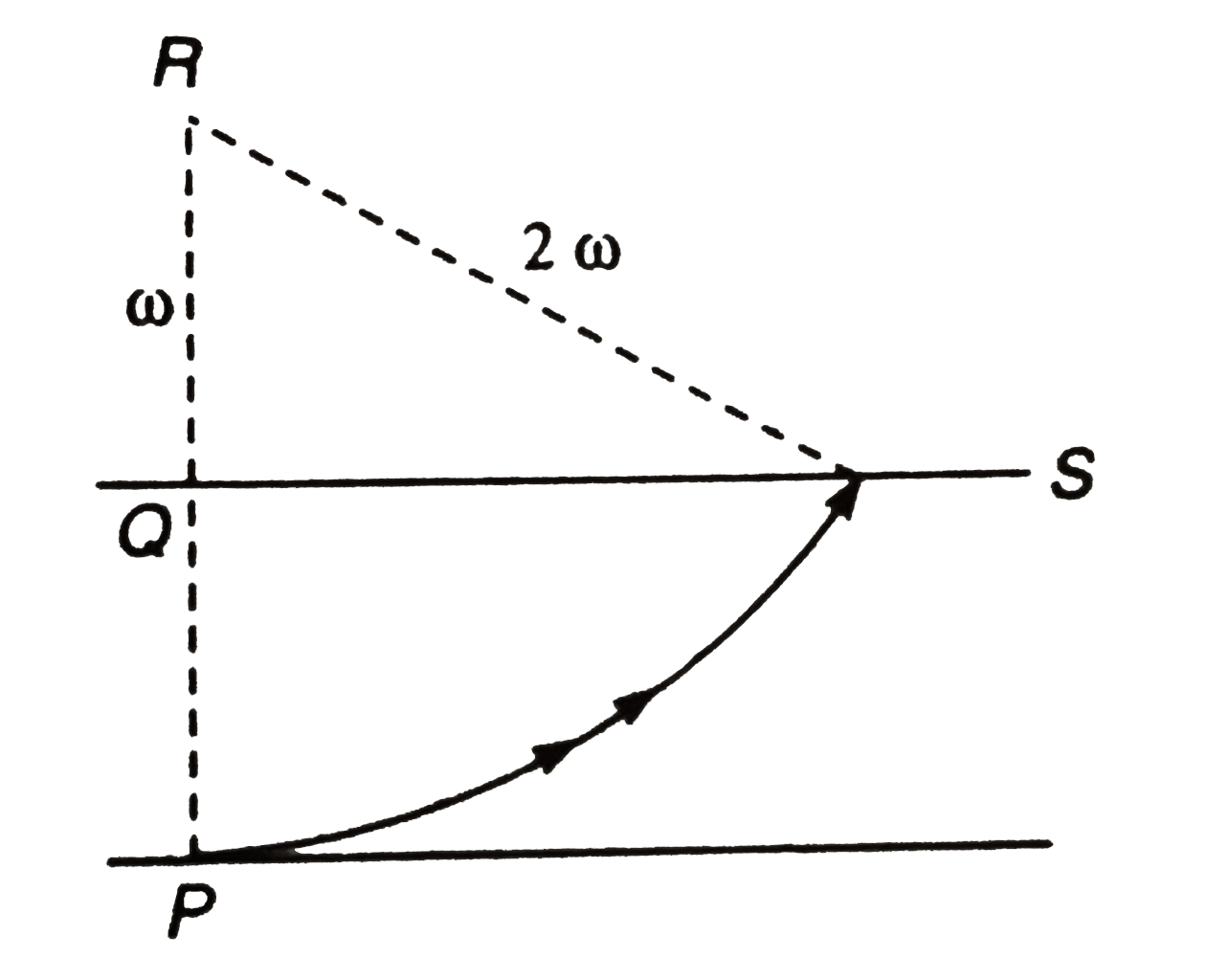
(b) Drifting =QS=√4ω2−ω2=√3ω.
(c) Suppose at any arbitrary time, the boat is at
point B.
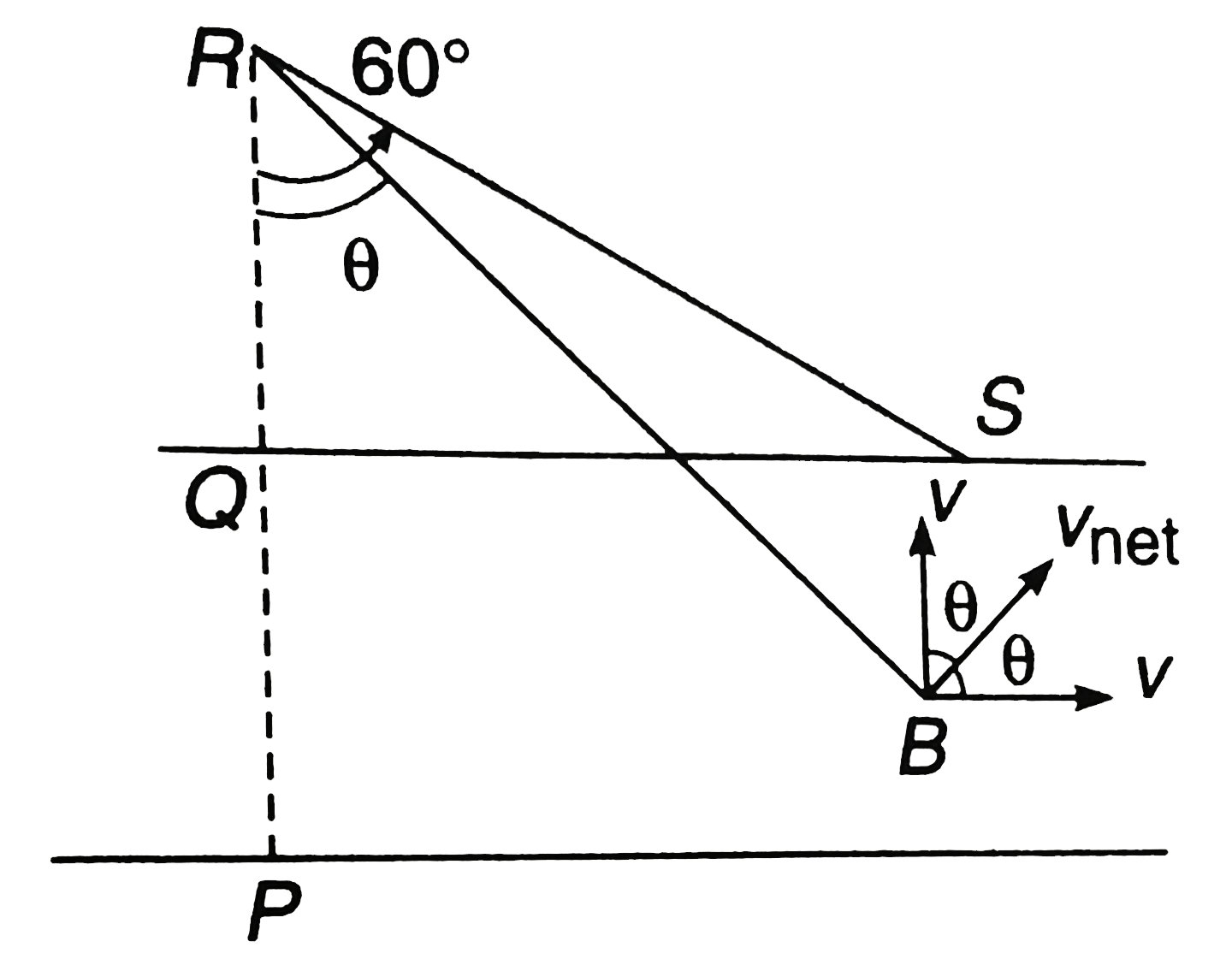
Vnet=2Vcosθ
dθdt=Vnet2ω=vcosθω
or ωvsecθdθ=dt
∴∫t0dt=ωv∫60∘0secθdθ
∴ωv[∈(secθ+tanθ]60∘0
or t=1.317ωv
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE
39 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE
23 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
River is flowing with a velocity vBR=4ˆim/s. A boat is moving with a velocity of vBR=(−2ˆi+4ˆj)m/s relative to river. The width of the river is 100m along y-direction. Choose the correct alternative(s)
View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The velocity of topmost point relative to the bottommost point is
View SolutionA river of width 80m is flowing at 6 m/s. A motorboat crosses the river in 10s and reaches a point directly across on the other river bank. The velocity of motorboat in still water is :
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionA river is flowing at 3m/s . A boat can move at 5m/s in still water. Boat starts from point A. Width of river is 120m. Select the incorrect statement :−
 .
.
View SolutionA river 500m wide is flowing at a rate of 4m/s. A boat is sailing at a velocity of 10m/s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View SolutionA river 400m wide is flowing at a rate of 2.0m/s. A boat is sailing at a velocity of 10.0m/s with respect to the water In a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
View SolutionThe river 500 m wide is flowing with a current of 4kph. A boat starts from one bank of the river wishes to cross the river at right angle to stream direction. Boatman can row the boat at 8 kph. In which direction he should row the boat. What time he ''ll take to cross the river ?
View SolutionA boat stems in a river with velocity 2ˆi+ˆj with respecitve to the ground. The river water flows with a velocity −3ˆi−4ˆj with respect to the ground. What is the relative velocity of boat w.r.t river water ?
View Solution
