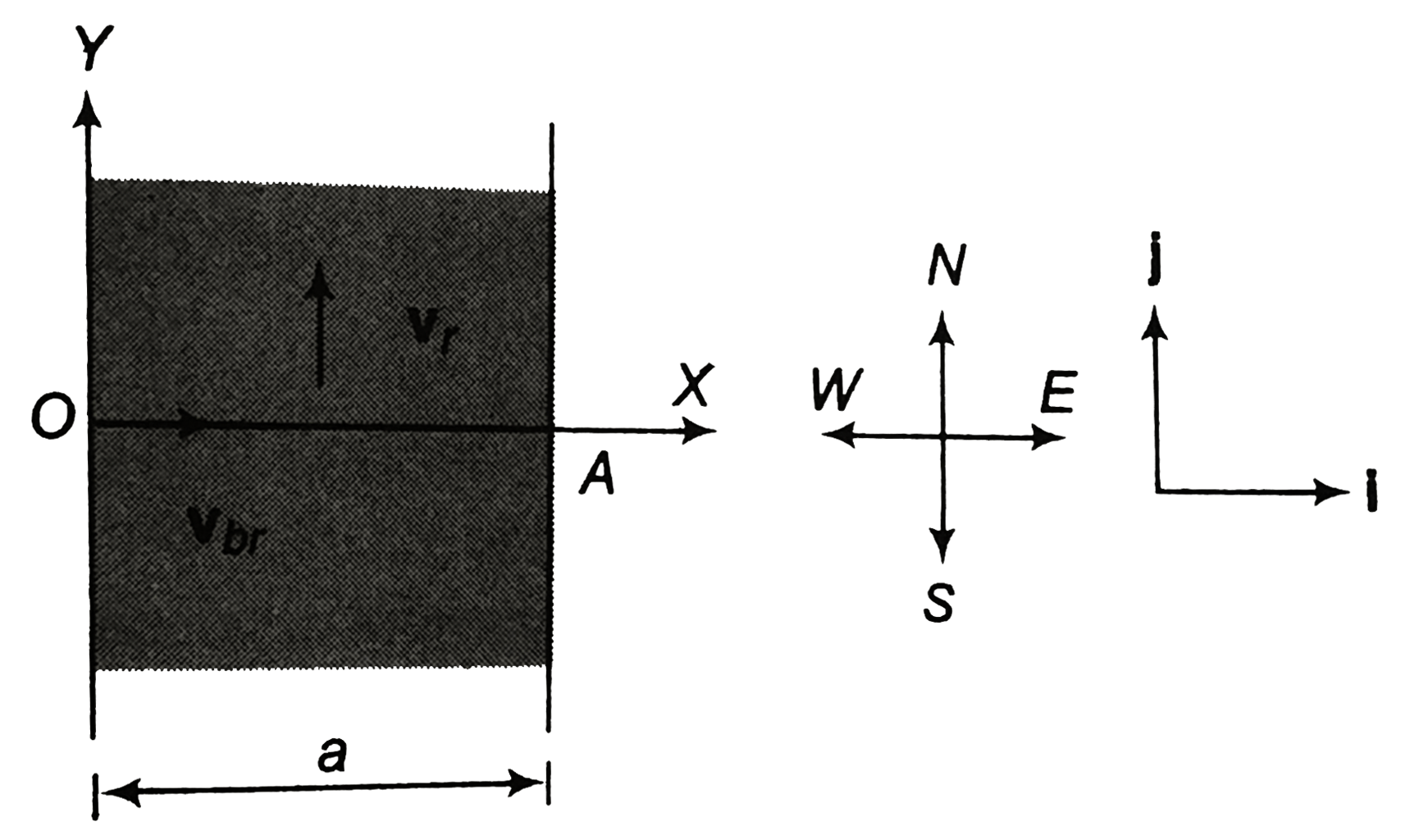
A river of width a with straight parallel banks flows due north with speed u. The points O and A are on opposite banks and A is due east of O. Coordinate axes Ox and Oy are taken in the east and north directions respectively. A boat, whose speed is v relative to water, starts from O and crosses the river. If the boat is steered due east and u varies with xas:u=x(a−x)va2. Find
(a) equation of trajectory of the boat,
(b) time taken to cross the river,
(c) absolute velocity of boatman when he reaches the opposite bank,
(d) the displacement of boatman when he reaches the opposite bank from the initial position.
The correct Answer is:A, B, C, D
(a) Let vbr be the velocity of boatman relative to
river, vr the velocity of river and vb is the absolute
velocity of boatman. Then,
vb=vbr+vr
Given, |vbr|=v and |vr|=u
Now u=vy=dydt=x(a−x)va2...(i)
and v=vx=dxdt....(ii)
Dividing Eq. (i) by (i), we get
dydx=x(a−x)a2ordy=x(a−x)a2dx
∫y0dy=∫x0x(a−x)a2dx
or y=x22a−x33a2.....(iii)
This is the desired equation of trajectory.
(b) Time taken to cross the river is
t=avx=av
(c) When the boatman reaches the opposite side,
x=aorvy=0 [From Eq.(i)]
Hence, resultant velocity of boatman is v along
positive x-axis or due east.
(d) From Eq. (iii)
y=a22a−a33a2=a6
At x=a (at opposite bank)
Hence, displacement of boatman will be
s=xˆi+yˆjors=aˆi+a6ˆj
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:SCQ_TYPE
Explore 39 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:MCQ_TYPE
Explore 23 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:Comprehension
Explore 7 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
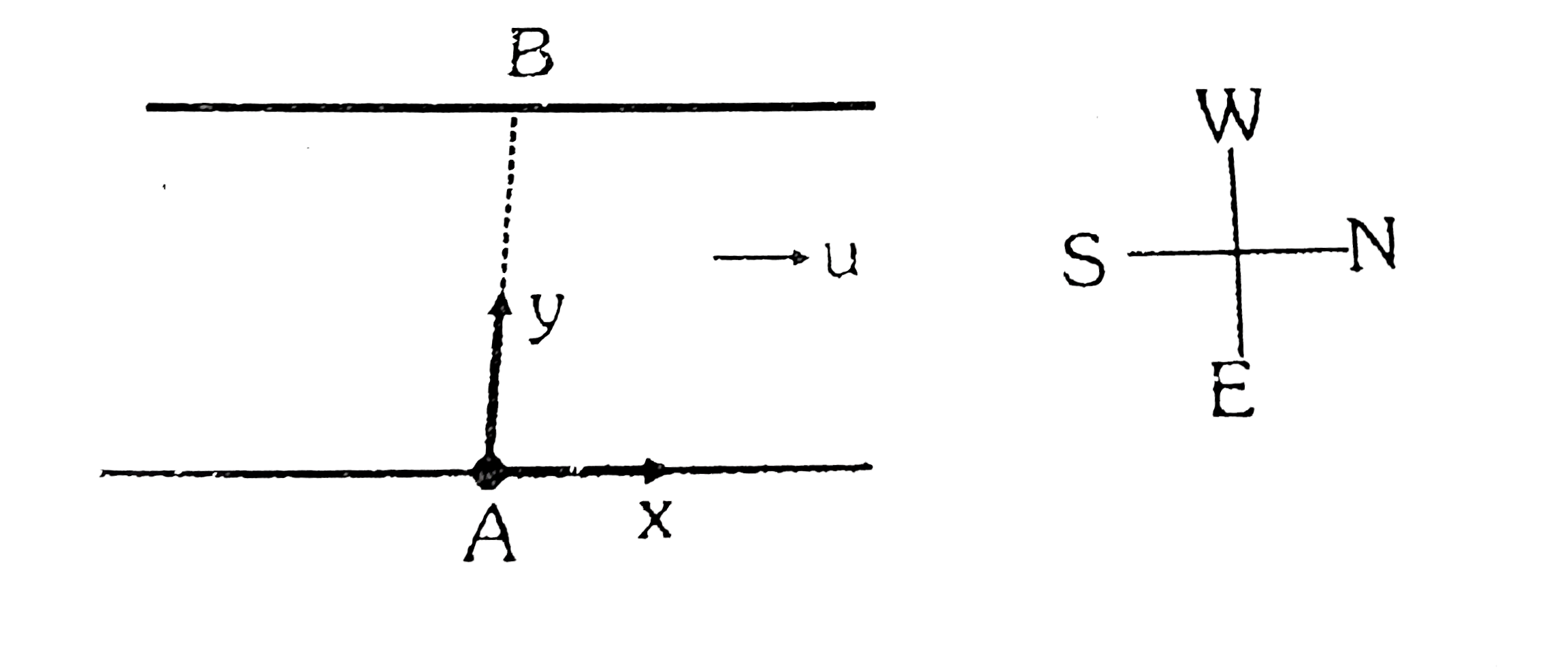
A river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
The time take by boat to cross the river is
View SolutionA river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
The time take by boat to cross the river is
View SolutionA river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
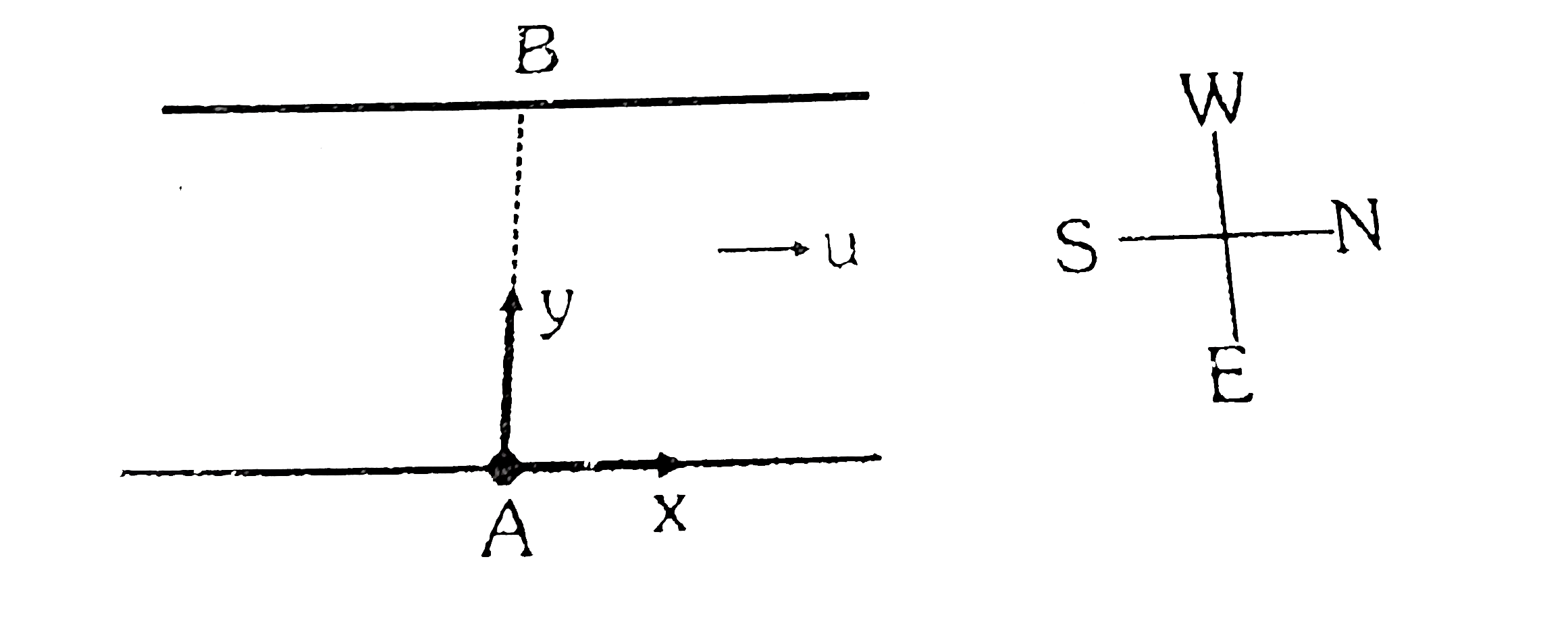
Equation of trajectory of the boat is
View SolutionA river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.

Absolute velocity of boat when it reaches the opposite bank is
A. 43v, towards East
B. v, towards West
C. 43v, towards West
D. →v, towards East
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View SolutionVelocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?

View SolutionA river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?
View SolutionA river 500m wide is flowing at a rate of 4m/s. A boat is sailing at a velocity of 10m/s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View SolutionA man goes 10m due east and then 24 m due north. Find the distance from the starting point.
View Solution