A man wishes to cross a river of width 120 m by a motorboat. His rowing speed in still water is 3m/s and his maximum walking speed is 1m/s. The river flows with velocity of 4m/s.
(a) Find the path which he should take to get to the point directly opposite to his starting point in the shortest time.
(b) Also, find the time which he takes to reach his destination.
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the situation step by step.
Given Data:
- Width of the river (d) = 120 m
- Speed of the boat in still water (v_b) = 3 m/s
- Speed of the river (v_r) = 4 m/s
- Walking speed of the man (v_w) = 1 m/s
(a) Finding the Path to Take
1. Understanding the Boat's Motion:
- The boat's speed can be broken down into two components:
- vbx=vbcosθ (across the river)
- vby=vbsinθ (downstream due to the river's current)
2. Setting Up the Equations:
- The man wants to reach the point directly opposite his starting point. This means that the downstream drift caused by the river must be countered by the upstream component of the boat's velocity.
- The effective downstream velocity due to the river and the boat's motion is:
veffective=vr−vby=4−3sinθ
3. Time to Cross the River:
- The time taken to cross the river can be expressed as:
t1=dvbx=1203cosθ
4. Distance Drifted Downstream:
- The distance drifted downstream while crossing is:
x=(vr−vby)⋅t1=(4−3sinθ)⋅1203cosθ
5. Walking to the Destination:
- After reaching the point downstream, the man will walk back to the opposite point with a speed of 1 m/s. The time taken to walk back is:
t2=xvw=(4−3sinθ)⋅1203cosθ1
6. Total Time:
- The total time T taken to reach the destination is:
T=t1+t2=1203cosθ+(4−3sinθ)⋅1203cosθ
- Simplifying this gives:
T=1203cosθ(1+(4−3sinθ))=120(5−3sinθ)3cosθ
7. Minimizing Time:
- To minimize time, take the derivative of T with respect to θ and set it to zero:
dTdθ=0
- This leads to finding sinθ=35 and consequently cosθ=45.
(b) Finding the Time Taken
1. Substituting Values:
- Substitute sinθ and cosθ into the total time equation:
T=120(5−3⋅35)3⋅45=120(5−95)125=120⋅165125=120⋅1612=160 seconds
Final Answer:
- Path: The man should row at an angle θ such that sinθ=35 and cosθ=45.
- Time Taken: 160 seconds or 2 minutes and 40 seconds.
- Width of the river (d) = 120 m
- Speed of the boat in still water (v_b) = 3 m/s
- Speed of the river (v_r) = 4 m/s
- Walking speed of the man (v_w) = 1 m/s
1. Understanding the Boat's Motion:
- The boat's speed can be broken down into two components:
- vbx=vbcosθ (across the river)
- vby=vbsinθ (downstream due to the river's current)
- The man wants to reach the point directly opposite his starting point. This means that the downstream drift caused by the river must be countered by the upstream component of the boat's velocity.
- The effective downstream velocity due to the river and the boat's motion is:
veffective=vr−vby=4−3sinθ
- The time taken to cross the river can be expressed as:
t1=dvbx=1203cosθ
- The distance drifted downstream while crossing is:
x=(vr−vby)⋅t1=(4−3sinθ)⋅1203cosθ
- After reaching the point downstream, the man will walk back to the opposite point with a speed of 1 m/s. The time taken to walk back is:
t2=xvw=(4−3sinθ)⋅1203cosθ1
- The total time T taken to reach the destination is:
T=t1+t2=1203cosθ+(4−3sinθ)⋅1203cosθ
- Simplifying this gives:
T=1203cosθ(1+(4−3sinθ))=120(5−3sinθ)3cosθ
- To minimize time, take the derivative of T with respect to θ and set it to zero:
dTdθ=0
- This leads to finding sinθ=35 and consequently cosθ=45.
1. Substituting Values:
- Substitute sinθ and cosθ into the total time equation:
T=120(5−3⋅35)3⋅45=120(5−95)125=120⋅165125=120⋅1612=160 seconds
- Path: The man should row at an angle θ such that sinθ=35 and cosθ=45.
- Time Taken: 160 seconds or 2 minutes and 40 seconds.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE39videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE23videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
A man can swim at the rate of 5kmh−1 in still water A. One km wide river flows at the rate of 3kmh−1 . The man wishes to swim across the river directly opposite to the starting point. How much time will be take to cross the river
View SolutionThe velocity of a boat in still water is 10 m/s. If water flows in the river with a velocity of 6 m/s what is the difference in times taken to cross the river in the shortest path and the shortest time. The width of the river is 80 m.
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5sec. his velocity in still water should be
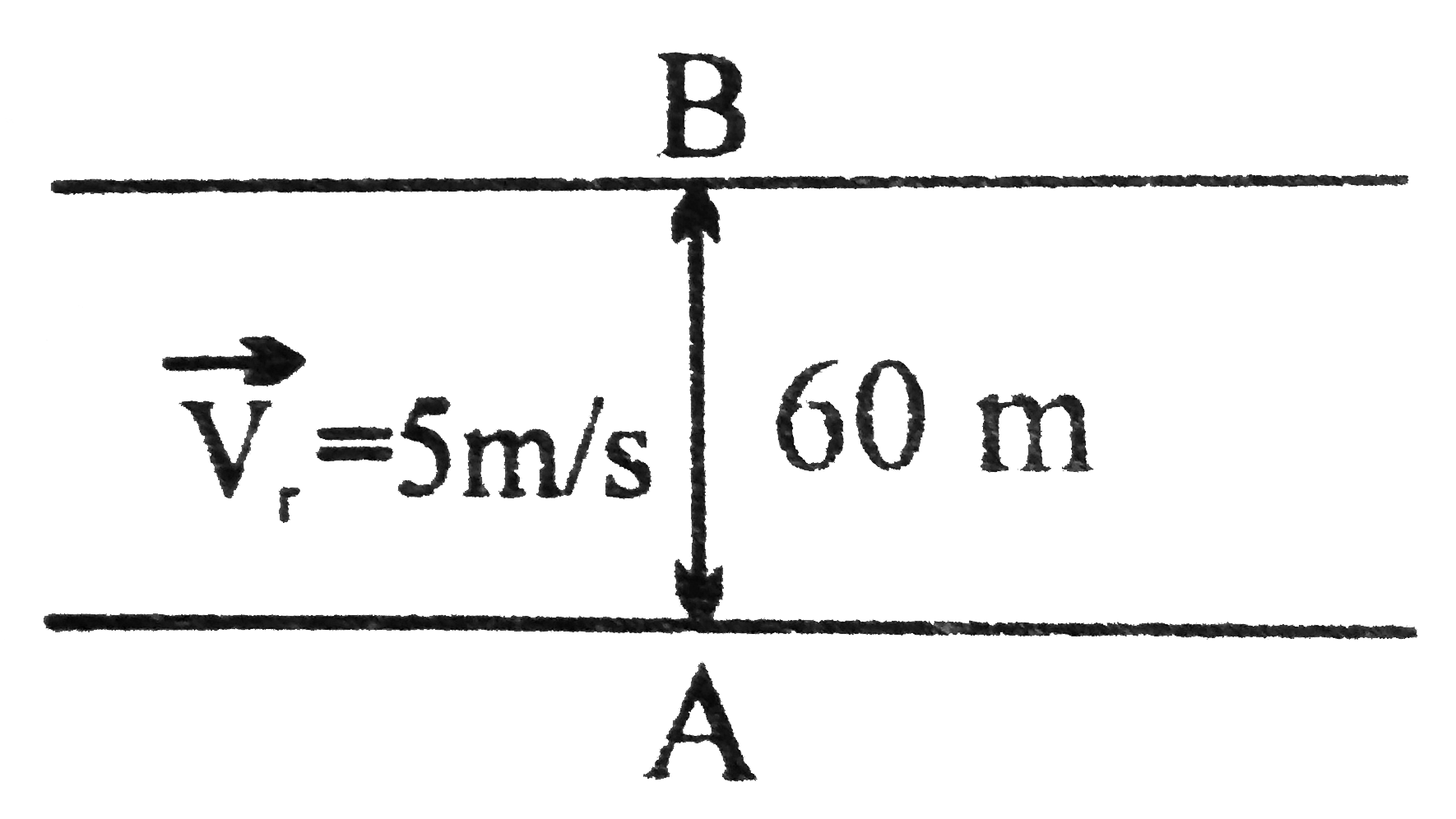 View Solution
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
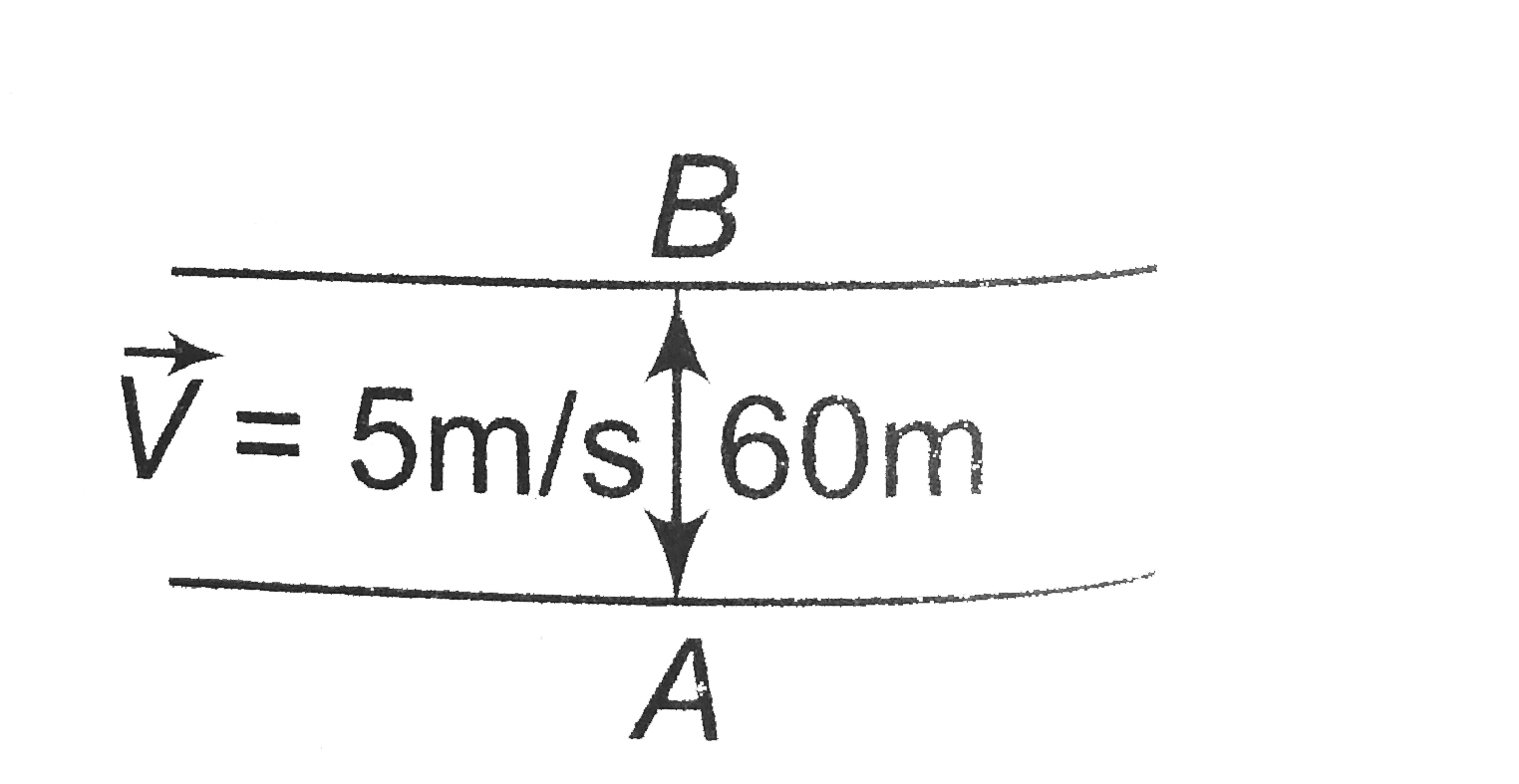 View Solution
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
 View Solution
View SolutionVelocity of boat in still water is 13 m/s. If water flows ina river with a velocity of 5 m/s. What is the difference in times taken by him to cross the river in the shortest path and in the shortest time. If the width of the river is 10 m.
View SolutionA swimmer wishes to cross a 500m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionA swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionA man can swim in still water at 4m/s river is flowing at 2m/s. the angle with downstream at which he should swim to cross the river minimum drift is
View SolutionA swimmer wants to cross a 200 m wide river which is flowing at a speed of 2 m/s. the velocity of the swimmer with respect to the river is 1 m/s. how far from the point directly opposite to the starting point does the swimmer reach the opposite bank ?
View Solution
