A river of width 80m is flowing at 6 m/s. A motorboat crosses the river in 10s and reaches a point directly across on the other river bank. The velocity of motorboat in still water is :
(a)8 m/s
(b)10 m/s
(c)6 m/s
(d)5 m/s
The correct Answer is:b
To solve the problem, we need to determine the velocity of the motorboat in still water given the width of the river, the speed of the river, and the time taken to cross the river.
1. Identify Given Data:
- Width of the river (D) = 80 m
- Speed of the river (Vr) = 6 m/s
- Time taken to cross the river (T) = 10 s
2. Calculate the Velocity of the Motorboat Across the River:
- The velocity of the motorboat across the river (Vb_perpendicular) can be calculated using the formula:
Vbperpendicular=DT
- Substituting the values:
Vbperpendicular=80m10s=8m/s
3. Use the Pythagorean Theorem to Find the Velocity of the Motorboat in Still Water:
- The velocity of the motorboat in still water (Vb) can be found using the Pythagorean theorem, as the velocities form a right triangle:
Vb2=Vb2perpendicular+Vr2
- Substituting the known values:
Vb2=(8m/s)2+(6m/s)2
Vb2=64+36
Vb2=100
4. Calculate the Velocity of the Motorboat in Still Water:
- Taking the square root of both sides:
Vb=√100=10m/s
5. Conclusion:
- The velocity of the motorboat in still water is 10 m/s.
- Width of the river (D) = 80 m
- Speed of the river (Vr) = 6 m/s
- Time taken to cross the river (T) = 10 s
- The velocity of the motorboat across the river (Vb_perpendicular) can be calculated using the formula:
Vbperpendicular=DT
- Substituting the values:
Vbperpendicular=80m10s=8m/s
- The velocity of the motorboat in still water (Vb) can be found using the Pythagorean theorem, as the velocities form a right triangle:
Vb2=Vb2perpendicular+Vr2
- Substituting the known values:
Vb2=(8m/s)2+(6m/s)2
Vb2=64+36
Vb2=100
- Taking the square root of both sides:
Vb=√100=10m/s
- The velocity of the motorboat in still water is 10 m/s.
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 2
65 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Main ( ARCHIVE ) ( LEVEL-1)
12 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Videos
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)
5 Videos
Similar Questions
A man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5sec. his velocity in still water should be
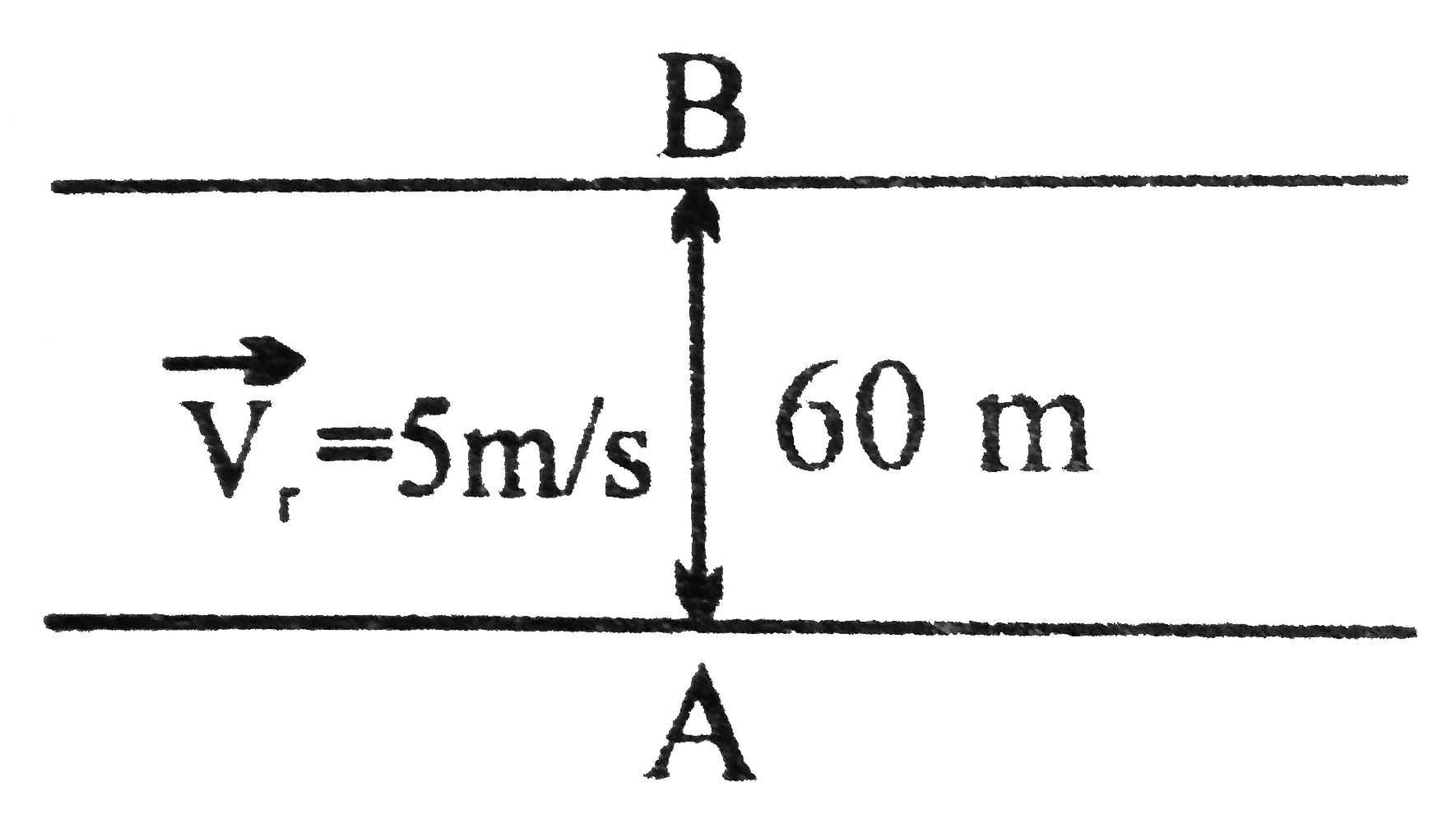
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
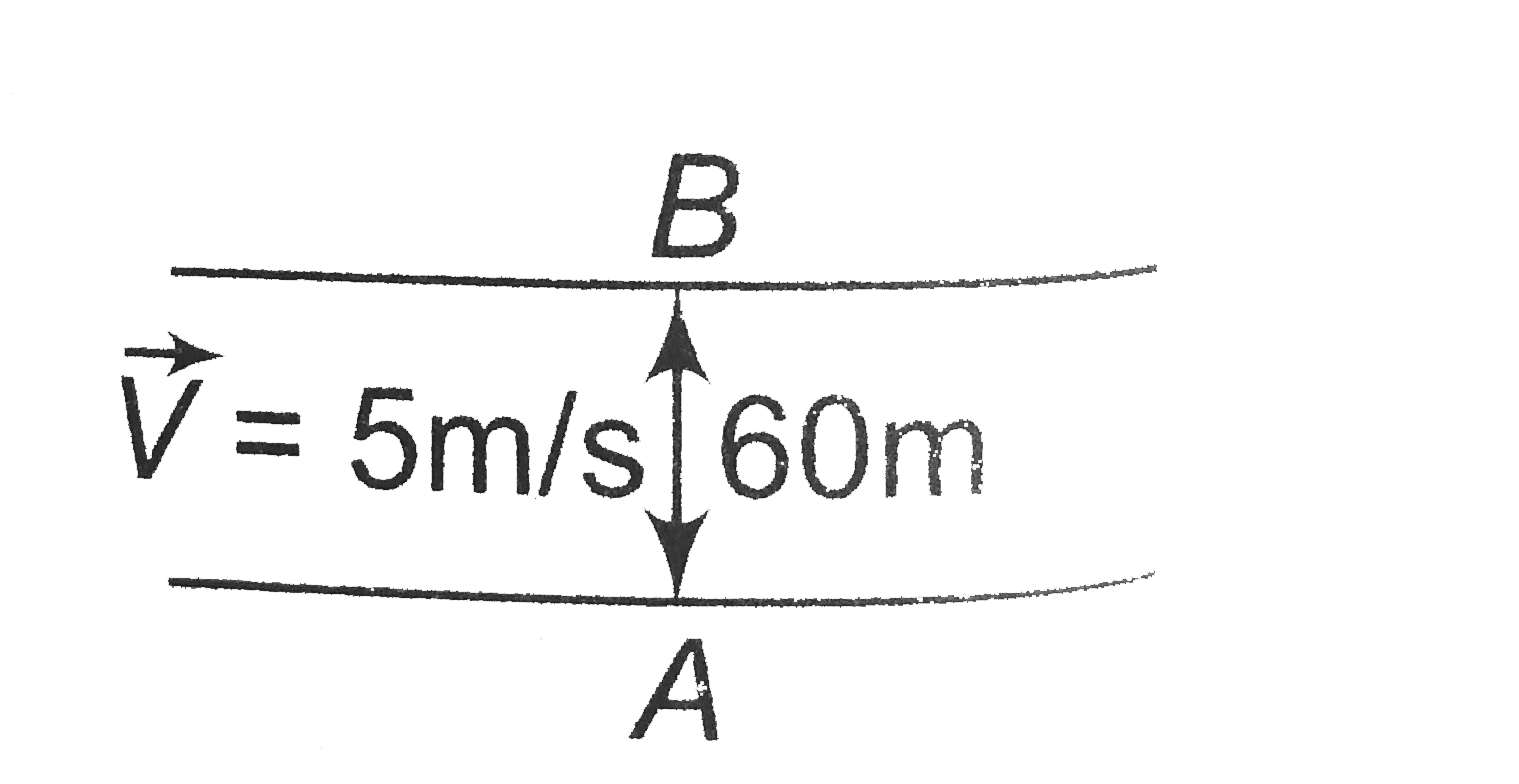
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be

View SolutionA river is flowing with velocity 5km/hr as shown in the figure. A boat start from A and reaches the other bank by covering shortest possible distance. Velocity of boat in still water is 3km/hr. The distance boat covers is.

View SolutionA man wishes to cross a river in a boat. If he crosses the river in minimum time he takes 10min with a drift of 120m. If he crosses the river taking shortest route, he takes 12.5min. Find the velocity of the boat with respect to water.
View SolutionA man crosses a river in a boat. If he cross the river in minimum time he takes 10min with a drift 120m. If he crosses the river taking shortest path, he takes 12.5min, find
(a) width of the river
(b) velocity of the boat with respect to water
(c) speed of the current
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionA river is flowing with a velocity of 2m/s. If the width of river in 100 m and swimmer wants to cross river is shortest time, what time (in sec) would he take if velocity of swimmer in still water is 4 m/s ?
View SolutionA person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
View SolutionA river 500m wide is flowing at a rate of 4m/s. A boat is sailing at a velocity of 10m/s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View Solution
