A very long, straight, thin wire carries −3.60nCm−1 of fixed negative charge. The wire is to be surrounded by a uniform cylinder of positive charge, radius 1.50 cm, coaxial with the wire. The volume charge density ρ of the cylinder is to be selected so that the net electric field outside the cylinder is zero. Calculate the required positive charge density ρ (in μCm−3).
6
7
5
3
The correct Answer is:C
To solve the problem, we need to find the volume charge density ρ of the positive charge cylinder that surrounds a long straight wire with a negative linear charge density λ. The goal is to ensure that the net electric field outside the cylinder is zero.
1. Identify the Given Values:
- Linear charge density of the wire: λ=−3.60nC/m=−3.60×10−9C/m
- Radius of the cylinder: r=1.50cm=1.50×10−2m
2. Electric Field Due to the Wire:
The electric field E at a distance r from a long straight wire with linear charge density λ is given by:
Ewire=λ2πϵ0r
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
3. Electric Field Due to the Cylinder:
The electric field outside a uniformly charged cylinder with linear charge density λ′ is given by:
Ecylinder=λ′2πϵ0r
4. Condition for Zero Net Electric Field:
For the net electric field outside the cylinder to be zero, the electric fields due to the wire and the cylinder must be equal in magnitude and opposite in direction:
Ewire+Ecylinder=0
This implies:
λ2πϵ0r+λ′2πϵ0r=0
Simplifying gives:
λ+λ′=0⇒λ′=−λ
5. Relating Linear Charge Density to Volume Charge Density:
The linear charge density λ′ of the cylinder can be expressed in terms of the volume charge density ρ as follows:
λ′=ρ⋅V
where V is the volume of the cylinder. The volume V of a cylinder can be calculated as:
V=πr2L
where L is the length of the cylinder. Thus,
λ′=ρ⋅πr2L
6. Substituting for λ′:
From the previous step, we have:
−λ=ρ⋅πr2
Rearranging gives:
ρ=−λπr2
7. Calculating ρ:
Substitute the values for λ and r:
ρ=−−3.60×10−9π(1.50×10−2)2
Calculate π(1.50×10−2)2:
π(1.50×10−2)2≈3.14×(2.25×10−4)≈7.068×10−4
Now substituting this back:
ρ=3.60×10−97.068×10−4≈5.09×10−6C/m3
8. Convert to Microcoulombs per Cubic Meter:
ρ≈5.09μC/m3
Final Answer:
The required positive charge density ρ is approximately 5.09μC/m3.
- Linear charge density of the wire: λ=−3.60nC/m=−3.60×10−9C/m
- Radius of the cylinder: r=1.50cm=1.50×10−2m
The electric field E at a distance r from a long straight wire with linear charge density λ is given by:
Ewire=λ2πϵ0r
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
The electric field outside a uniformly charged cylinder with linear charge density λ′ is given by:
Ecylinder=λ′2πϵ0r
For the net electric field outside the cylinder to be zero, the electric fields due to the wire and the cylinder must be equal in magnitude and opposite in direction:
Ewire+Ecylinder=0
This implies:
λ2πϵ0r+λ′2πϵ0r=0
Simplifying gives:
λ+λ′=0⇒λ′=−λ
The linear charge density λ′ of the cylinder can be expressed in terms of the volume charge density ρ as follows:
λ′=ρ⋅V
where V is the volume of the cylinder. The volume V of a cylinder can be calculated as:
V=πr2L
where L is the length of the cylinder. Thus,
λ′=ρ⋅πr2L
From the previous step, we have:
−λ=ρ⋅πr2
Rearranging gives:
ρ=−λπr2
Substitute the values for λ and r:
ρ=−−3.60×10−9π(1.50×10−2)2
Calculate π(1.50×10−2)2:
π(1.50×10−2)2≈3.14×(2.25×10−4)≈7.068×10−4
Now substituting this back:
ρ=3.60×10−97.068×10−4≈5.09×10−6C/m3
ρ≈5.09μC/m3
The required positive charge density ρ is approximately 5.09μC/m3.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Higher Order Thinking Skills
7 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - NCERT Exemplar
5 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Application Of Gauss Law
9 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
If the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
View SolutionA solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformaly charged line charge( linear charge density λ) is placed along the ctlinder axis. If electric field intensity vector outside the cylinder is zerom then :
View SolutionAn early model for an atom considered it to have a positively charged point nucleus of charge Ze, surrounded by a uniform density of negative charge upto a radius R. The atom as a whole is neutral. The electric field at a distance r from the nucleus is (r < R)

View SolutionFigure shows a long wire having uniform charge density λ as shown in figure. Calculate electric field intensity at point P.
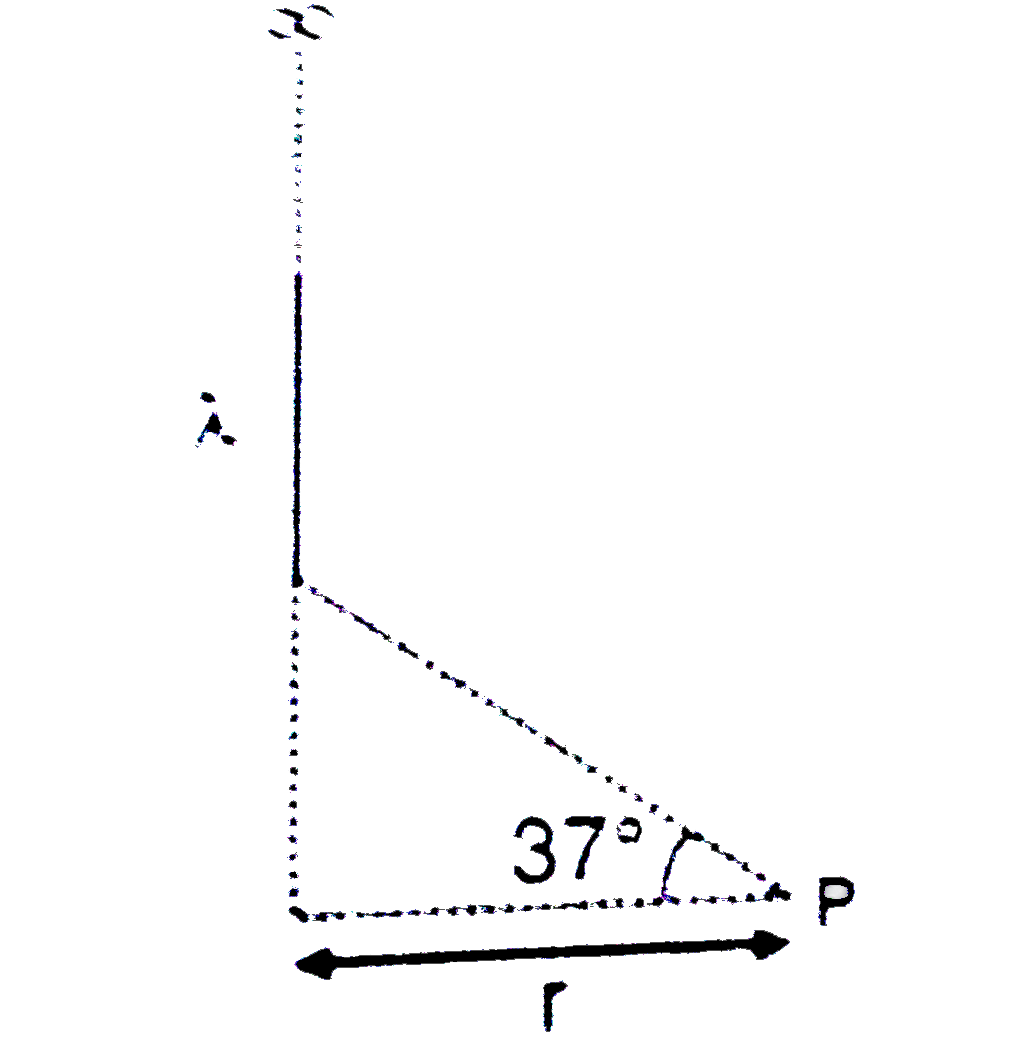
View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
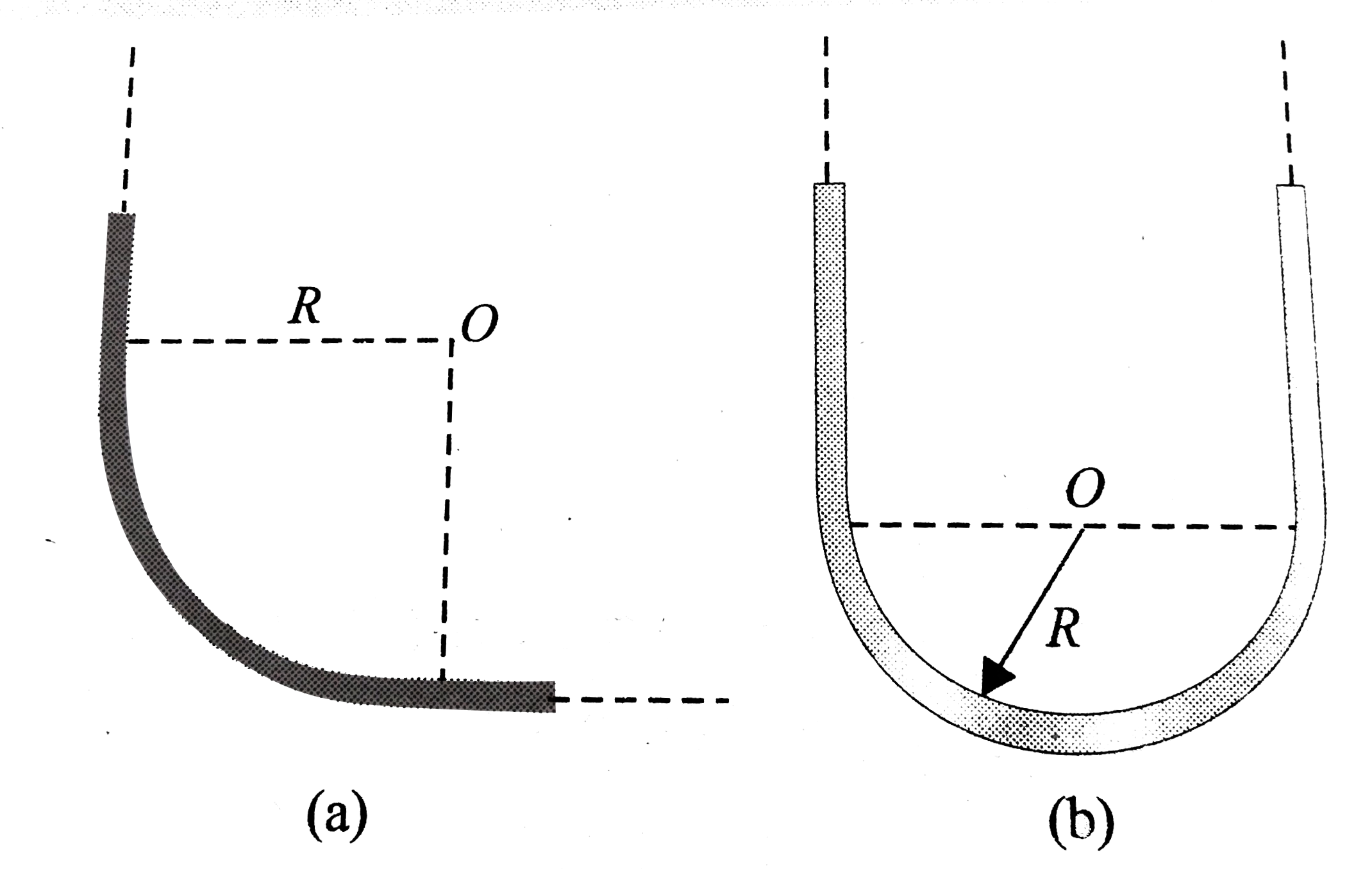
View SolutionA long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View SolutionA long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View SolutionAn infinite line charge is at the axis of a cylinder of length 1 m and radius 7 cm. If electric field at any point on the curved surface of cylinder is 250 NC−1, then net electric flux through the cylinder is
View Solution
