A long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
To find the electric field in the space between a long charged cylinder and a hollow coaxial conducting cylinder, we can follow these steps:
1. Identify the Configuration:
We have a long charged cylinder with a linear charge density λ and a hollow coaxial conducting cylinder surrounding it.
2. Consider a Length L:
To analyze the electric field, we will consider a segment of length L of the inner charged cylinder. The total charge on this segment is given by:
Q=λL
3. Understand the Conducting Cylinder:
The hollow conducting cylinder will have an induced charge on its inner surface due to the electric field created by the inner charged cylinder. This induced charge will be equal in magnitude but opposite in sign to the charge on the inner cylinder, which is −λL.
4. Apply Gauss's Law:
To find the electric field in the region between the two cylinders, we will use Gauss's Law, which states:
∮E⋅dA=Qencϵ0
where Qenc is the charge enclosed by the Gaussian surface.
5. Choose a Gaussian Surface:
We will choose a cylindrical Gaussian surface of radius r (where r is the distance from the axis of the inner cylinder and R1<r<R2, with R1 being the radius of the inner cylinder and R2 being the radius of the outer cylinder). The area of the curved surface of the cylinder is:
A=2πrL
6. Calculate the Enclosed Charge:
The charge enclosed by our Gaussian surface is just the charge on the inner cylinder:
Qenc=λL
7. Substitute into Gauss's Law:
The left-hand side of Gauss's Law can be expressed as:
∮E⋅dA=E⋅A=E⋅(2πrL)
Thus, we have:
E⋅(2πrL)=λLϵ0
8. Solve for the Electric Field E:
Now, we can solve for E:
E=λ2πrϵ0
Final Result:
The electric field in the space between the two cylinders is given by:
E=λ2πrϵ0
We have a long charged cylinder with a linear charge density λ and a hollow coaxial conducting cylinder surrounding it.
To analyze the electric field, we will consider a segment of length L of the inner charged cylinder. The total charge on this segment is given by:
Q=λL
The hollow conducting cylinder will have an induced charge on its inner surface due to the electric field created by the inner charged cylinder. This induced charge will be equal in magnitude but opposite in sign to the charge on the inner cylinder, which is −λL.
To find the electric field in the region between the two cylinders, we will use Gauss's Law, which states:
∮E⋅dA=Qencϵ0
where Qenc is the charge enclosed by the Gaussian surface.
We will choose a cylindrical Gaussian surface of radius r (where r is the distance from the axis of the inner cylinder and R1<r<R2, with R1 being the radius of the inner cylinder and R2 being the radius of the outer cylinder). The area of the curved surface of the cylinder is:
A=2πrL
The charge enclosed by our Gaussian surface is just the charge on the inner cylinder:
Qenc=λL
The left-hand side of Gauss's Law can be expressed as:
∮E⋅dA=E⋅A=E⋅(2πrL)
Thus, we have:
E⋅(2πrL)=λLϵ0
Now, we can solve for E:
E=λ2πrϵ0
The electric field in the space between the two cylinders is given by:
E=λ2πrϵ0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )
8 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1
105 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
Two parallel infinite line charges +λand−λ are placed with a separation distance R in free space. The net electric field exactly mid-way between the two line charges is
View SolutionTwo parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformaly charged line charge( linear charge density λ) is placed along the ctlinder axis. If electric field intensity vector outside the cylinder is zerom then :
View SolutionAn infinite line charge of uniform electric charge density λ lies along the axis of an electrically conducting infinite cylindrical shell of radius R. At time t=0, the space inside the cylinder is filled with a material of permittivity ε and electrical conductivity σ. The electrical conduction in the material follows Ohm's law. Which one of the following graphs best describes the subsequent variation of the magnitude of current density j(t) at any point in the material ?
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
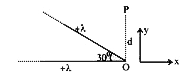
View SolutionTwo infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
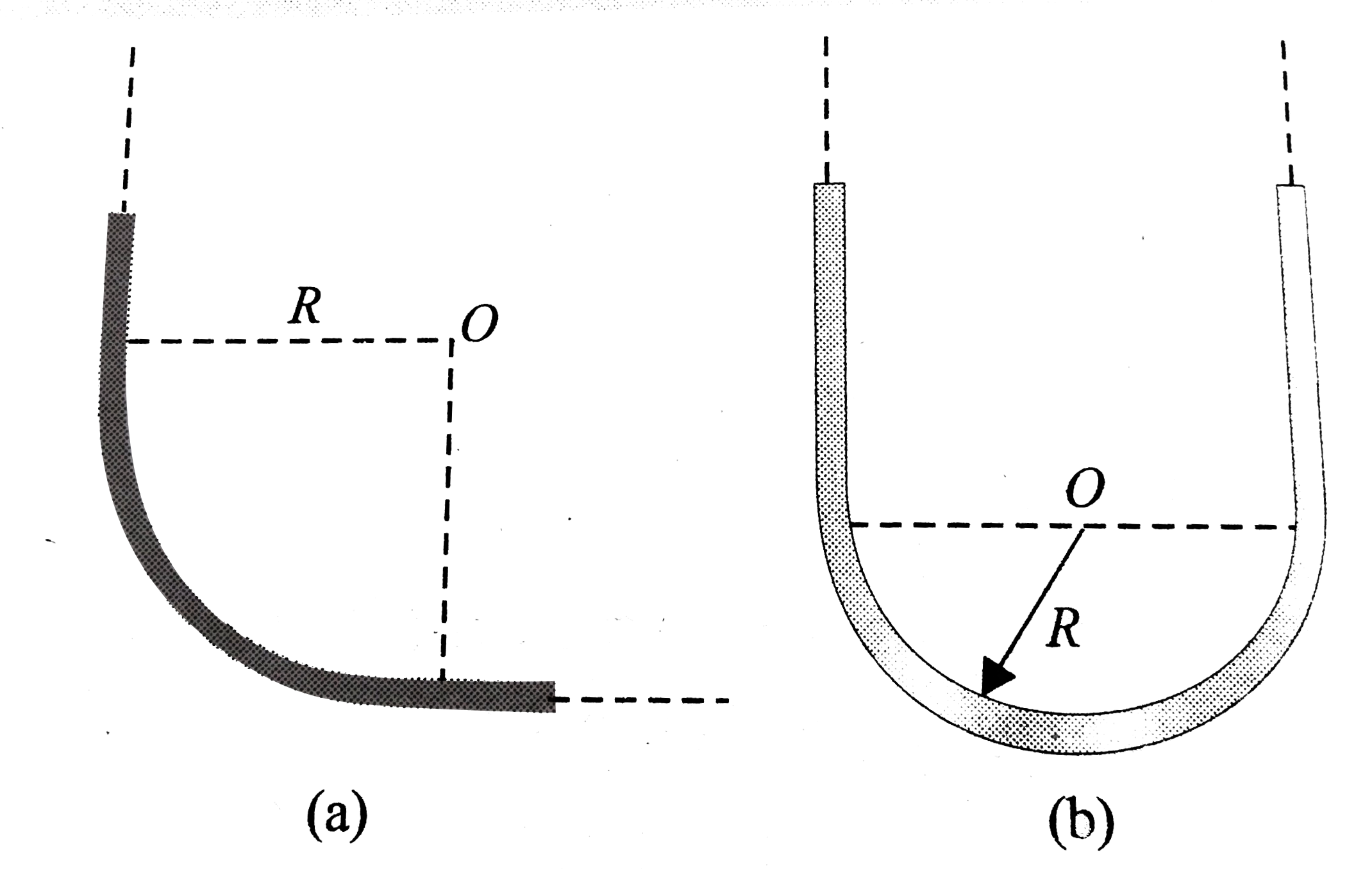
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
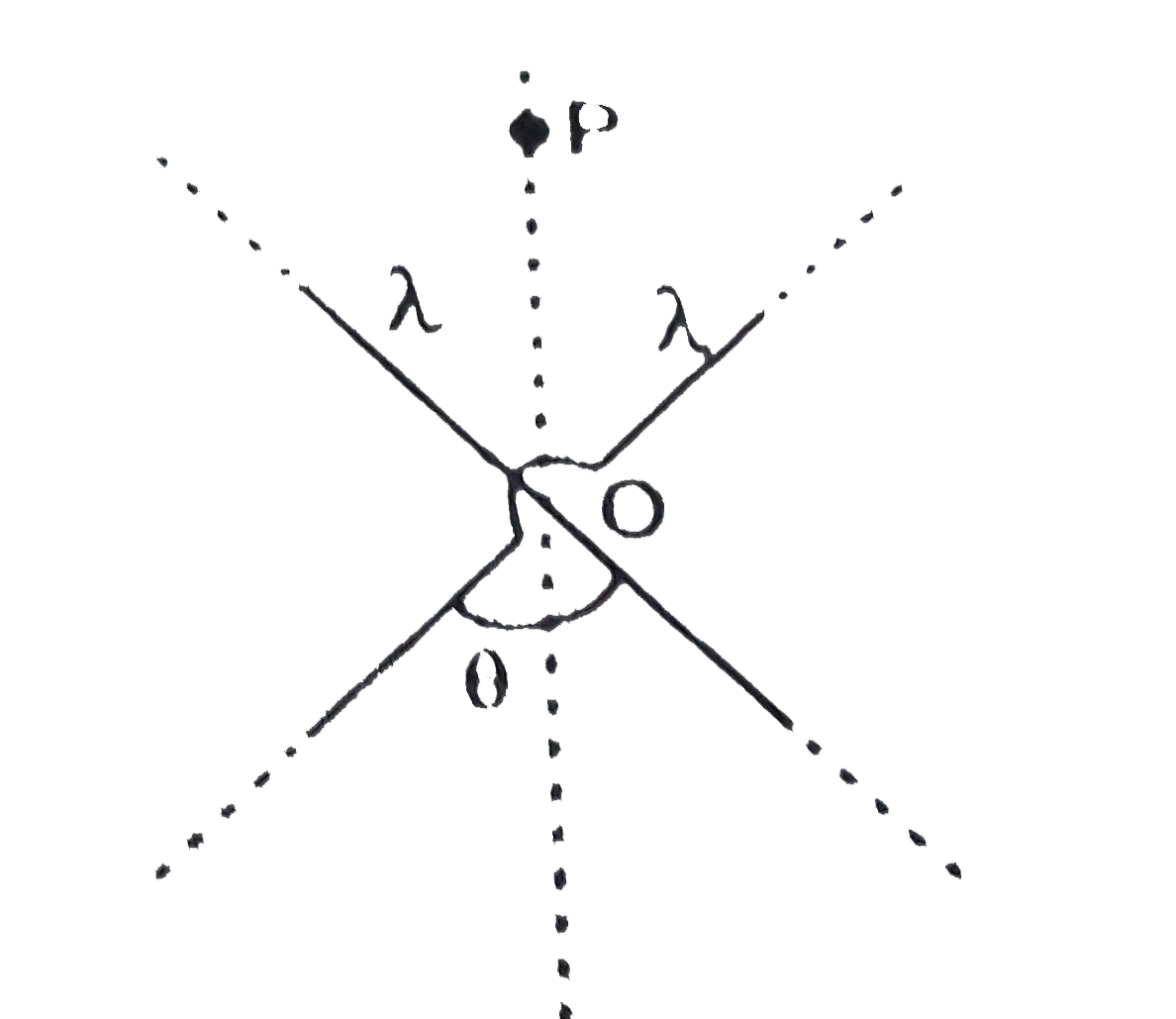
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.

View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View Solution
