A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is (σ/2ε0)ˆn , where ˆn is the unit vector in the outward normal direction, and σ is the surface charge density near the hole.
The correct Answer is:B
Surface charge density near the hole =σ . Unit vector n (normal directed outwards).
Let P be the point on the hole. The electric field at Point P closed to the surface of conductor, according to Gauss's theorem,
∫→E.¯¯¯¯ds=qe0
(∵=qds⇒q=0 ds, where ds= area) where, q is the charge near the hole. Edscosθ=adse0
∵ Angle between electric field and area vector is 0∘ ∴Eds=adse0=E=σe0⇒E=0e0n
This electric field is due to the filled up hole and the field due to the rest of the charged conductor. The two fields inside the conductor are equal and opposite. So, there is no electric field inside the conductor. Outside the conductor, the electric field at P due to each part =12E=σ2e0¯n

Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )8videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1105videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
Similar Questions
A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the holes is (σ/2ε0) ˆn, where ˆn is the unit vector in the outward normal direction, and σ is the surface charge density near the hole.
View SolutionShow that the electric field at the surface of a charged conductor is given by →E=σε0ˆn , where σ is the surface charge density and ˆn is a unit vector normal to the surface in the outward direction .
View SolutionThe electric field near a conducting surface having a uniform surface charge denstiy σ is given by
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionWhy the electric field at the outer surface of a hollow charged conductor is normal to the surface?
View SolutionThe surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the centre of the disc σ2∈0. With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc is
View SolutionA spherical charged conductor has surface charge density σ.The intensity of electric field and potential on its surface are E and V .Now radius of sphere is halved keeping the charge density as constant .The new electric field on the surface and potential at the centre of the sphere are
View SolutionA spherical charged conductor has surface density of charge as σ. The electric field intensity on its surface is E. If the radius of the surface is doubled, keeping σ uncharged, what will be the electric field intensity on the new sphere ?
View SolutionShow in the figure are two point charge + Q and - Q inside the cavity of the Spherical .shell the changes are kept near the surface of the cavity on opposite sides of the centre of the shell if σ1 is the surface charge on the inner surface and Q1 net charge on it and σ2 the surface charge on the outer surface and Q2 net charge on it then :
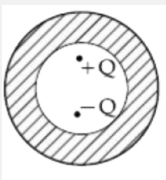 View Solution
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View Solution
