A long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
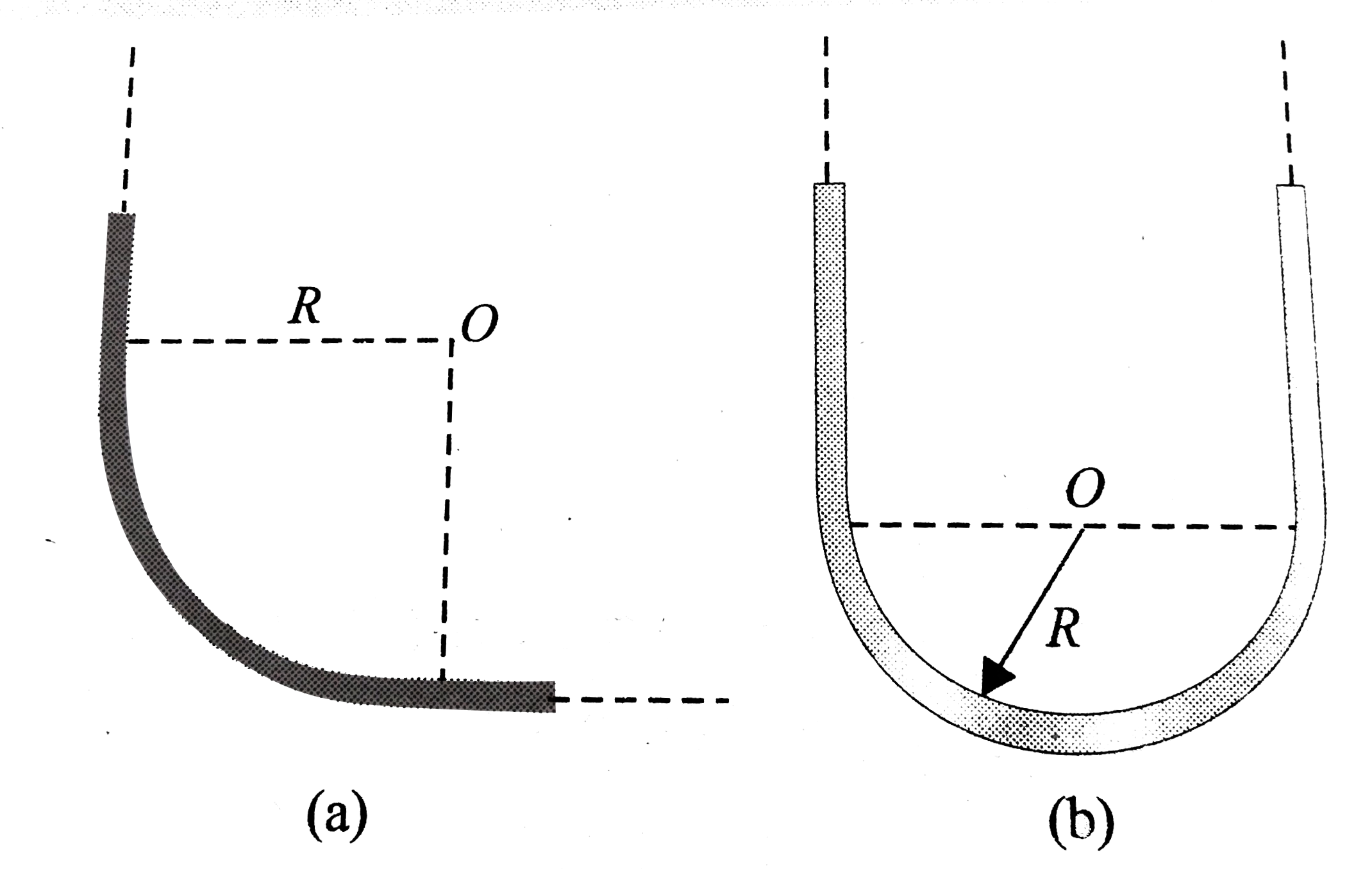
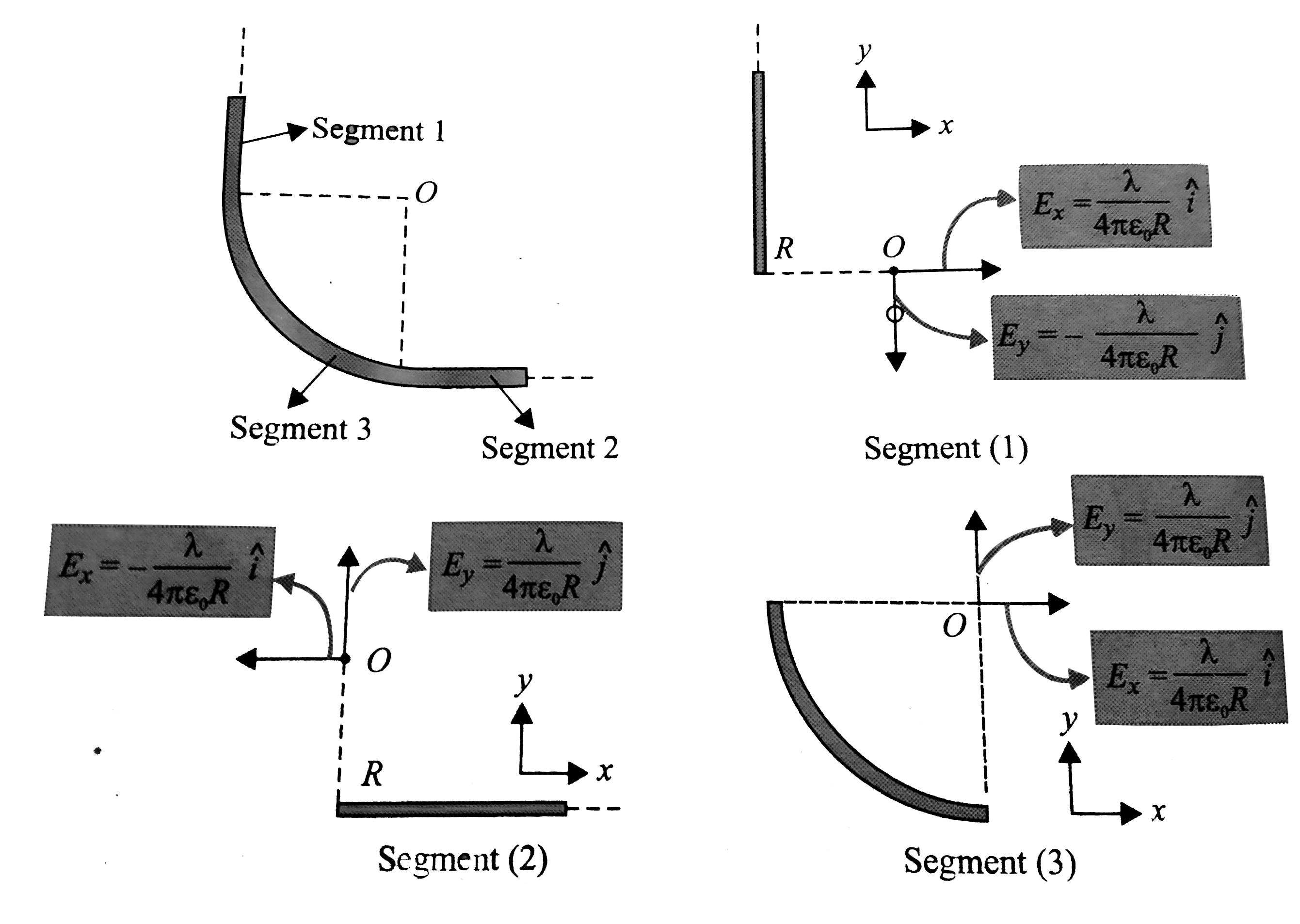
For Fig. Field due to segment 1 is
→E1=[λ4πε_(0)R]ˆi+[−λ4πε_(0)R]ˆj
field dur to segment 2 is
→E2=[λ4πε0R]ˆi+[−λ4πε0R]ˆj
Field due tp quater shape wire segment 3 is
→E3=[λ4πε_(0)R]ˆi+[−λ4πε_(0)R]ˆj(∴θ1=90∘,θ2=0∘)
 ,
, 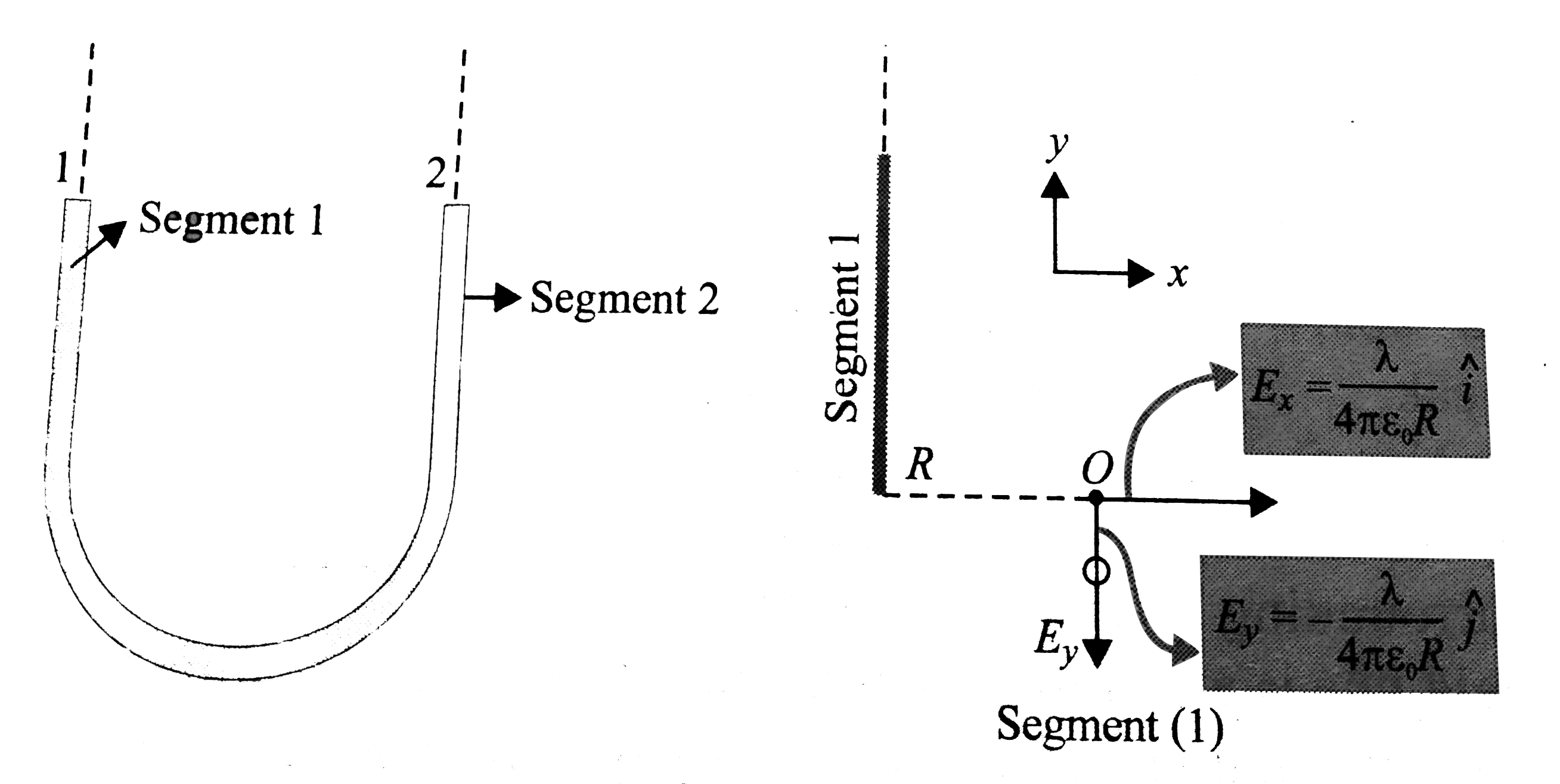
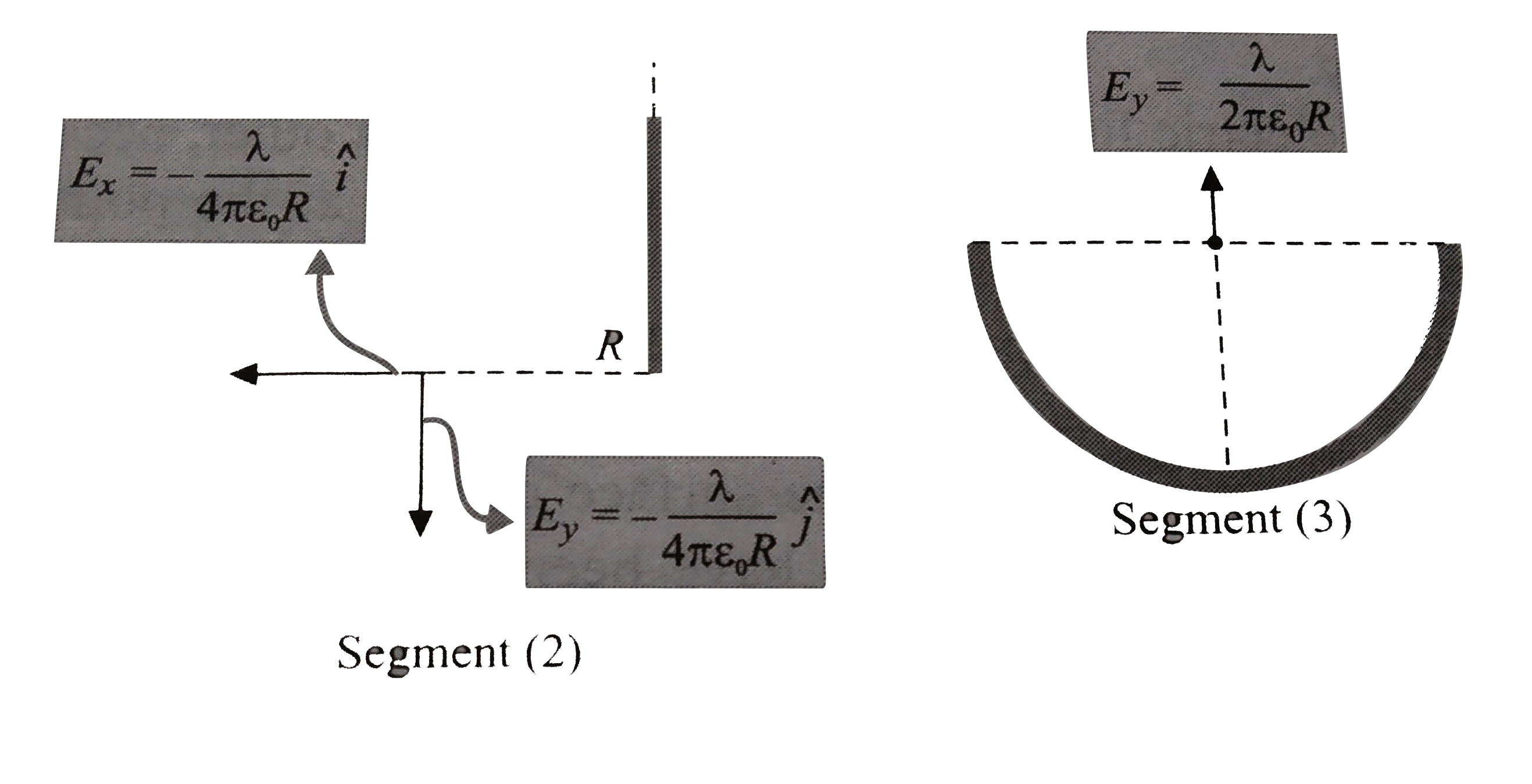 ,
,
The resultant field is the superpositon of the fields due to each part, i.e.
→E=→E1+→E2+→E3 ...(i)
Substituting the values of →E1,→E2, and →E3 in eq. (i) we get,
→E=[λ4πε0R]ˆi+[λ4πε0R]ˆj
∣∣→E1∣∣=[(λ4πε0R)2]+(λ4πε0R)2]1/2=√2λ4πε0R
here, Ex=Ey=λ4πε0R
Hence, the resulant field will make an angle of 45∘ with the axis.
(b). For fig. field due to segment 1 is
→E1=λ4πε0R[ˆi−ˆj]
Field due to segment 2 is
→Ex2=λ4πε0Rˆi
→Ey2=λ4πε0Rˆi
→E2=λ4πε0R[ˆi−ˆj]
Field due to segment 3 is
→E3=λ2πε0Rˆj
from the principle of superposition of electric fields.
→E=→E1+→E2+→E3
=λ4πε0R[ˆi−ˆj]−λ4πε0R[ˆi−ˆj]+λ2πε0R[ˆi−ˆj]=0
Hence, the net field is zero.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
An infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
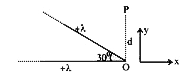
View SolutionFigure shows a long wire having uniform charge density λ as shown in figure. Calculate electric field intensity at point P.
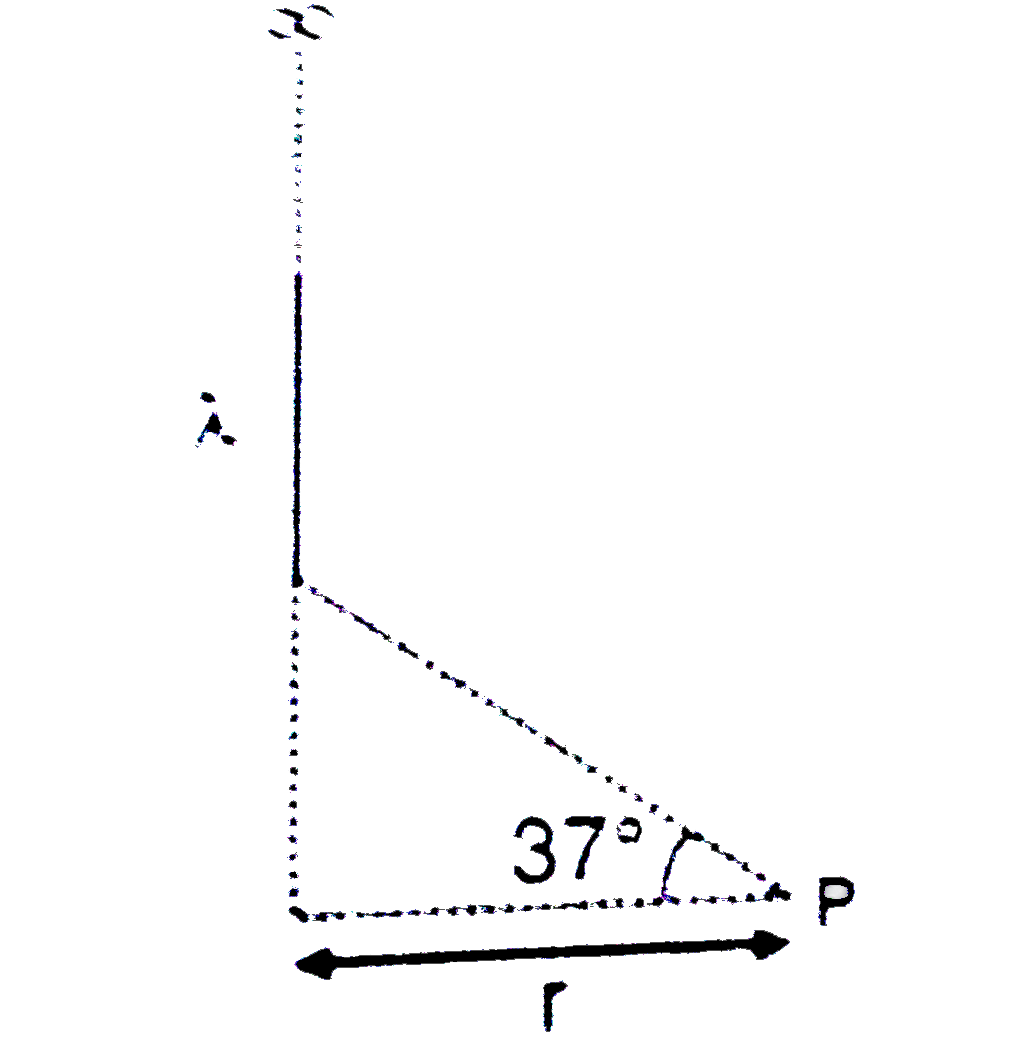
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
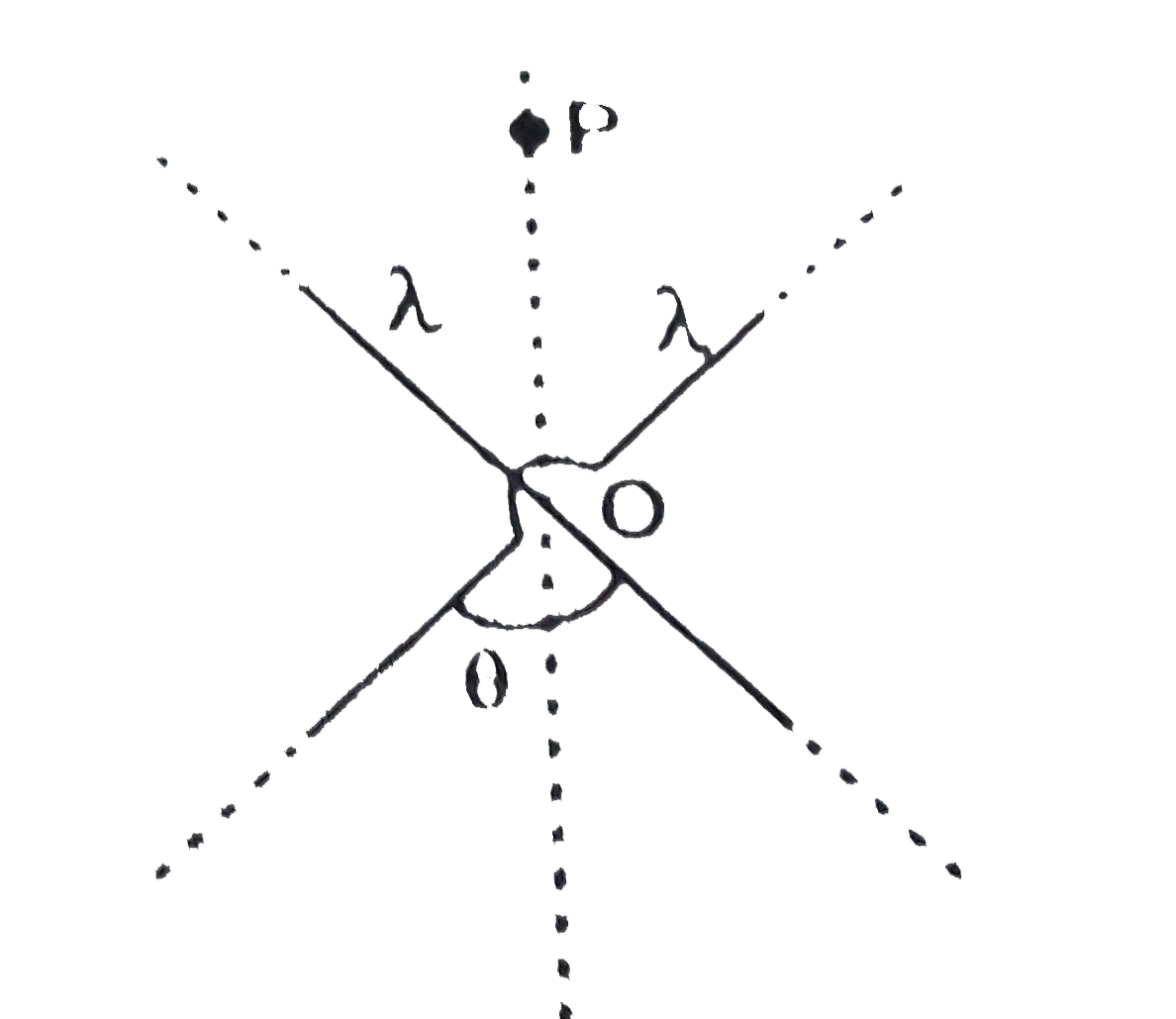
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.

View SolutionFor the arrangement shown in Fig. determine the magnetic field at centre O.

View SolutionDue to an electric dipole shown in fig., the electric field intensity is parallel to dipole axis :

View SolutionIf three infinite charged sheets of uniform surface charge densities σ,2σ and −4σ are placed as shown in figure, then find out electric field intensities at points A, B, C and D.

View SolutionShown in Fig. is a conductor carrying current I. Find the magnetic field intensity at point O.
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View Solution
