Figure shows a long wire having uniform charge density λ as shown in figure. Calculate electric field intensity at point P.
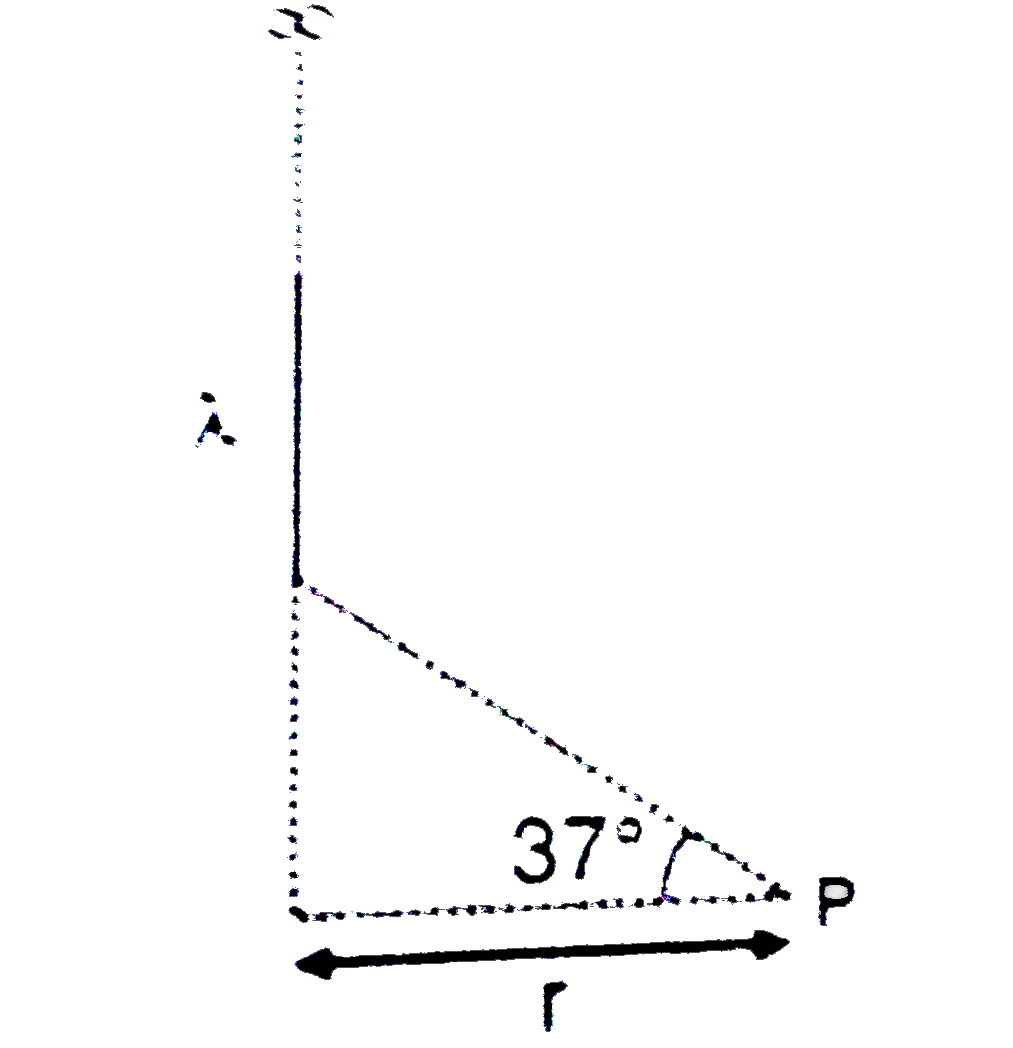
θ1=90º and θ2=360º−37º So
Ex=Kλr[sinθ1+sinθ2],Ey=Kλr[cosθ2−cosθ1]
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
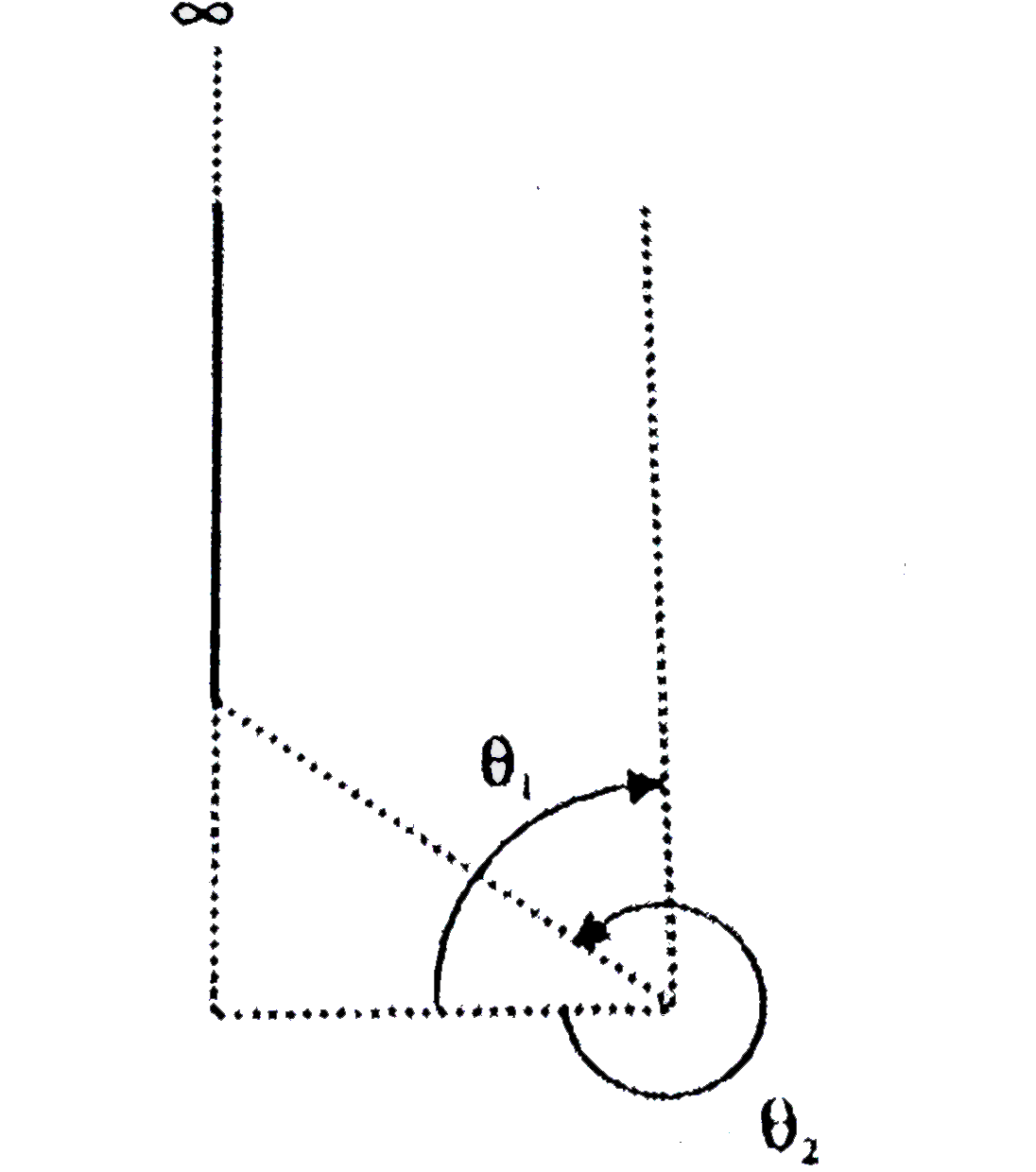
A long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
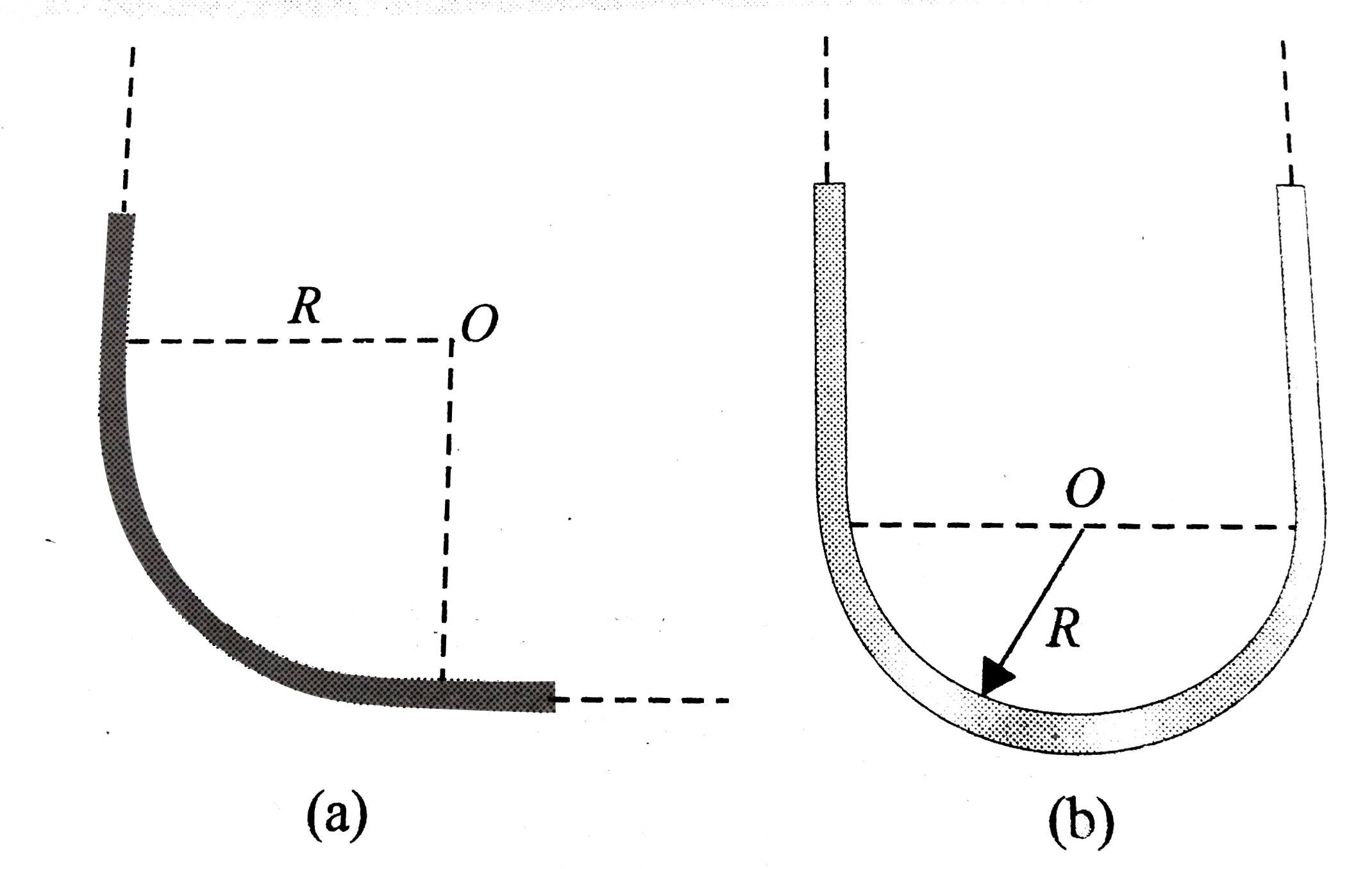
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
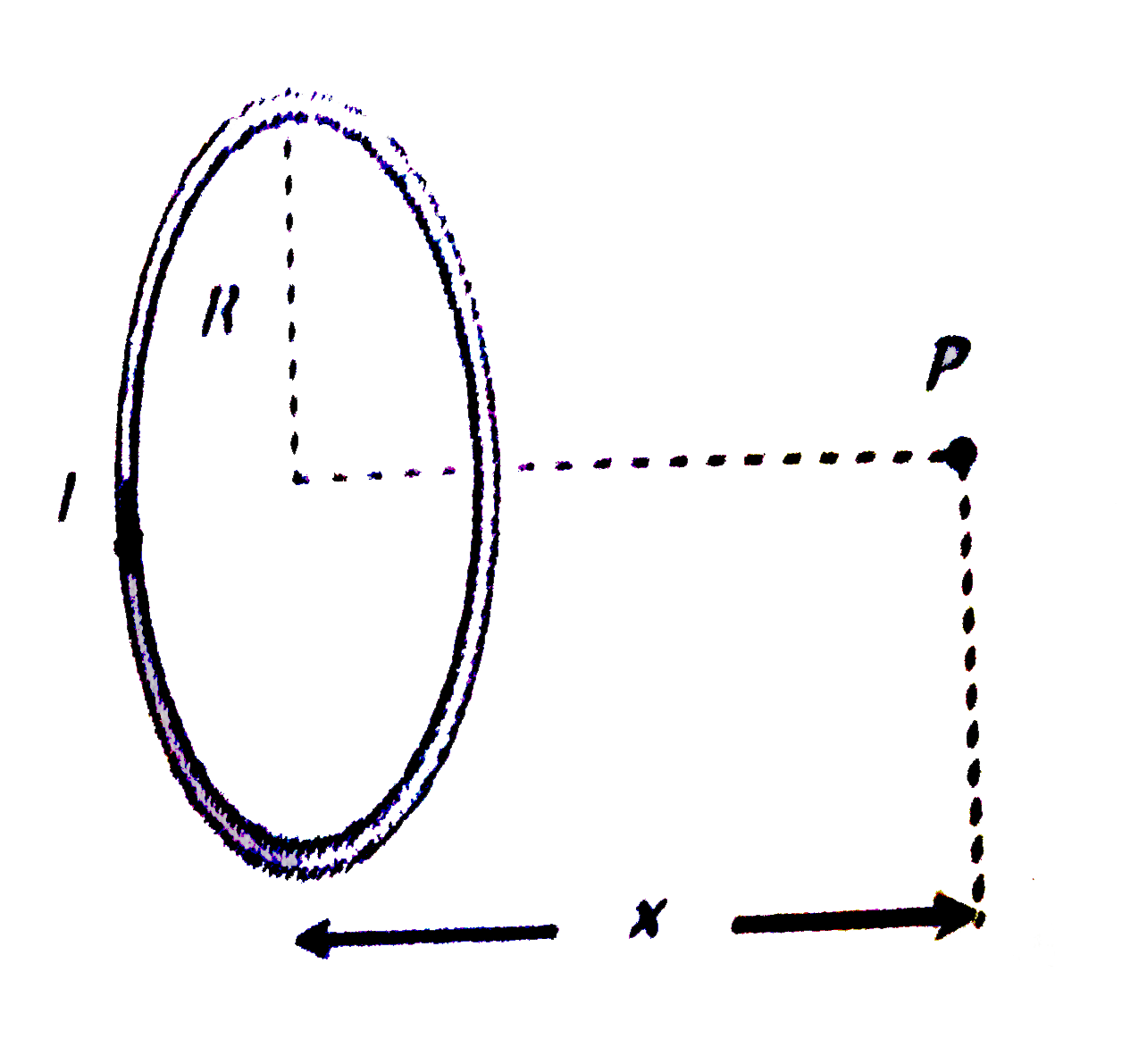
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
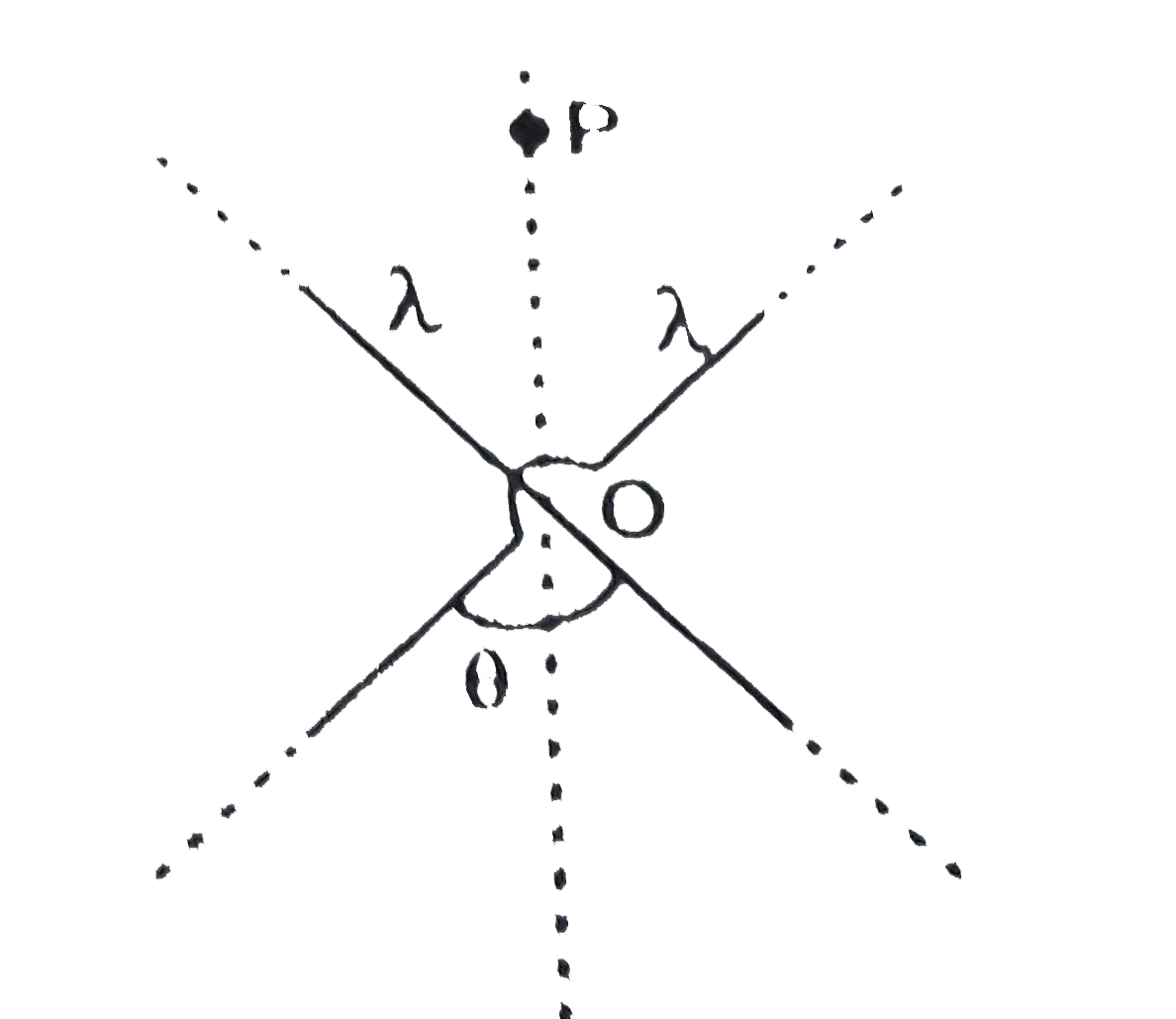
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.

View SolutionA wire AMB is placed along y-axis having linear charge density λ C/m. The electric field intensity at point P is ( PM=0.1 m)
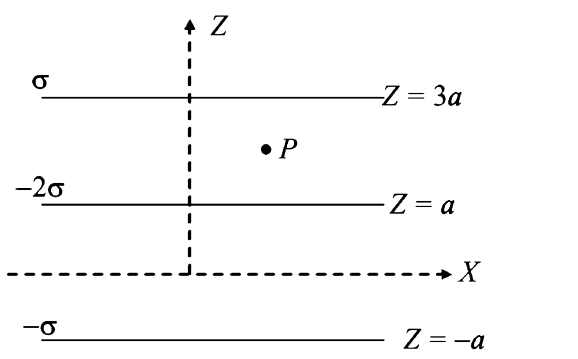
View SolutionThree infinitely long charge sheets are placed as shown in figure. The electric field at point P is
View SolutionIf linear charge density of a wire as shown in the figure is λ

View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -

View SolutionCharge 2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be somewhere

View Solution_2019_CBT4_E01_072_Q01.png)
Four charges are arranged on y axis as shown in figure. Then the electric field at point P is proportional to:
View Solution

