A charge is distributed with a linear density λ over a rod of the length L placed along radius vector drawn from the point where a point charge q is located. The distance between q and the nearest point on linear charge is R. The electrical force experienced by the linear charge due to q is
qλL4πε0R2
qλL4πε0R(R+L)
qλL4πε0RL
qλL4πε0L2
The correct Answer is:B
To solve the problem of finding the electrical force experienced by a linear charge due to a point charge, we can follow these steps:
Step 1: Understand the Setup
We have a linear charge distributed over a rod of length L with a linear charge density λ. This means that the total charge Q on the rod can be expressed as:
Q=λL
The rod is placed along a radius vector drawn from a point charge q, and the distance from the point charge to the nearest point on the linear charge is R.
Step 2: Define the Electric Field Due to the Point Charge
The electric field E created by the point charge q at a distance R is given by Coulomb's law:
E=k⋅|q|R2
where k is Coulomb's constant, approximately 8.99×109N m2/C2.
Step 3: Calculate the Force on the Linear Charge
The force F experienced by the linear charge due to the electric field can be calculated using the formula:
F=Q⋅E
Substituting for Q and E:
F=(λL)⋅(k⋅|q|R2)
Thus, the expression for the force becomes:
F=k⋅λL⋅|q|R2
Final Expression
The electrical force experienced by the linear charge due to the point charge q is:
F=k⋅λL⋅|q|R2
---
We have a linear charge distributed over a rod of length L with a linear charge density λ. This means that the total charge Q on the rod can be expressed as:
Q=λL
The rod is placed along a radius vector drawn from a point charge q, and the distance from the point charge to the nearest point on the linear charge is R.
The electric field E created by the point charge q at a distance R is given by Coulomb's law:
E=k⋅|q|R2
where k is Coulomb's constant, approximately 8.99×109N m2/C2.
The force F experienced by the linear charge due to the electric field can be calculated using the formula:
F=Q⋅E
Substituting for Q and E:
F=(λL)⋅(k⋅|q|R2)
Thus, the expression for the force becomes:
F=k⋅λL⋅|q|R2
The electrical force experienced by the linear charge due to the point charge q is:
F=k⋅λL⋅|q|R2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Higher Order Thinking Skills
7 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - NCERT Exemplar
5 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Application Of Gauss Law
9 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
A point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
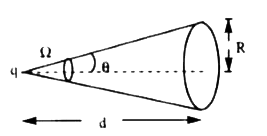
View SolutionA point charge q is placed at a distance r from a very long charged thread of unoform linear charge density λ. Find out total electric force experienced by the line charge due to the point charge. (Neglect gravity).
View SolutionA positive point charge q is placed at a distance 2 R from the surface of a metallic shell of radius R. the electric field at centre of shell due to indouced charge has magnitude
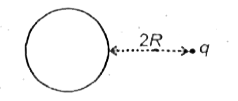
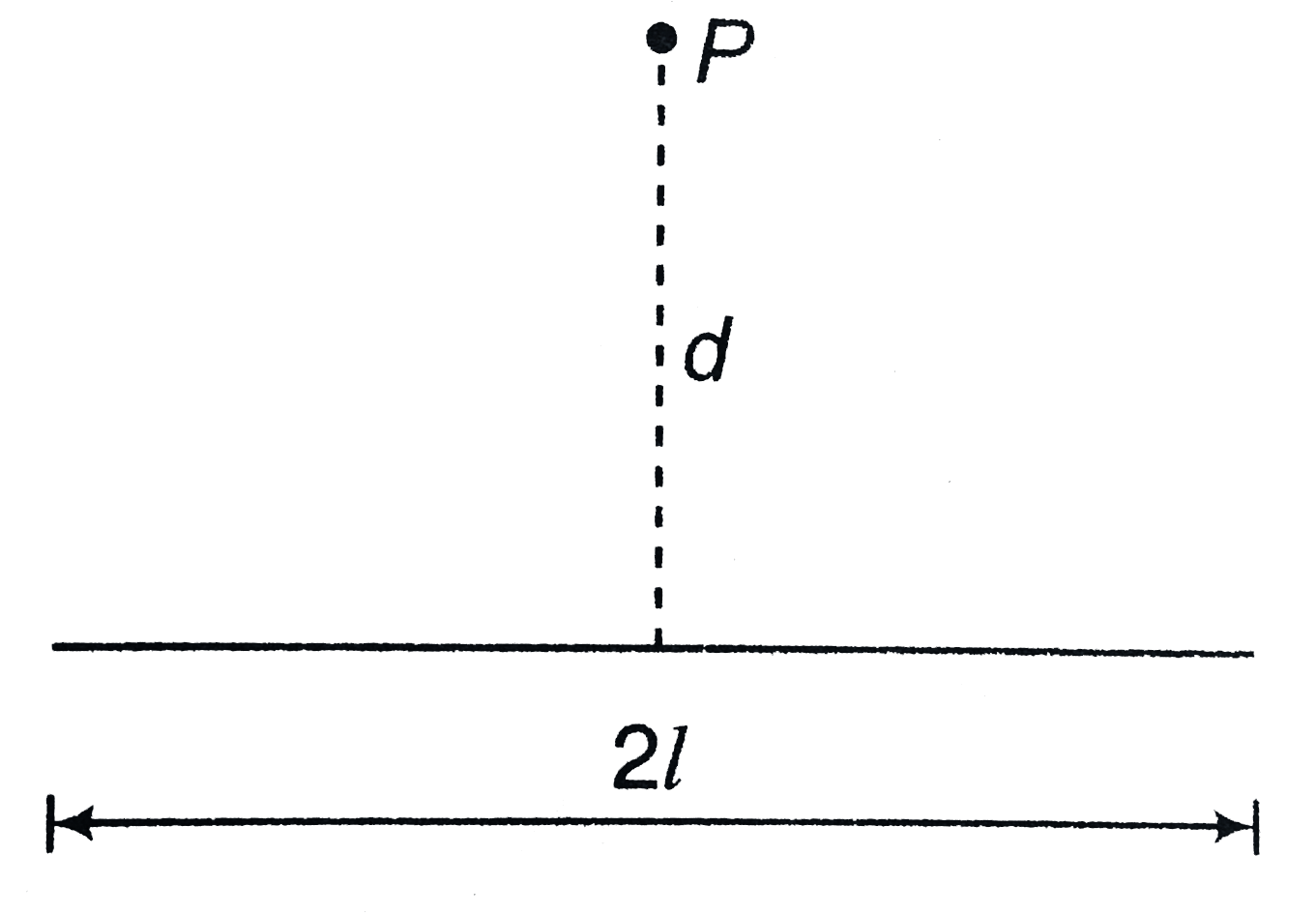
View SolutionA charge q is uniformly distributed along an insulating straight wire of length 2l as shown in Fig. Find an expression for the electric potential at a point located a distance d from the distribution along its perpendicular bisector.
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionThe point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionAn arc of radius r carries charge. The linear density of charge is λ and the arc subtends an angle π3 at the centre.
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.

View Solution
