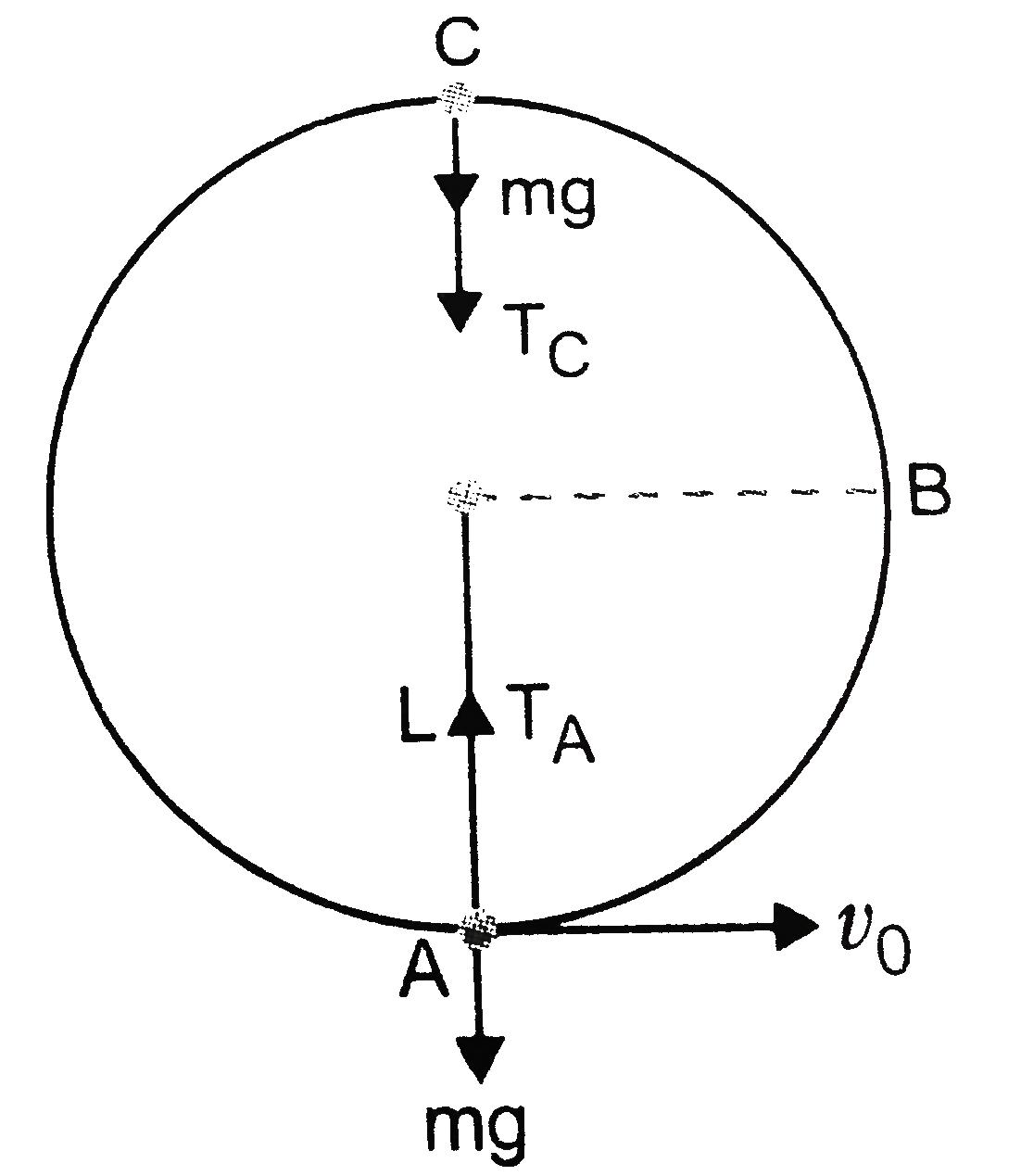
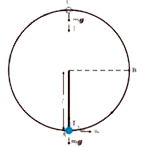
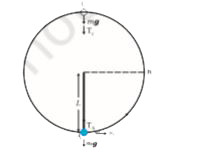
A bob of mass m is suspeded by a light string of length L . It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semicircular trajectroy in the vertical plane with the string becoming slack only on reaching the topmost point C . Thisis shown in figure .Obtain a expression for (i) v0 (ii) the ratio of the kinetic energies (KBKC) at B and C . Comment on the nature of the trajectroy of the bob after it reaches the point C .
 Solution in Gujrati
Solution in Gujrati
Two forces acting on bob. (i)Gravity and (ii) the tension T in the string .the work is not done by tension in the string .because dispalcement of bob is always normal to the string .
The potential energy of the bob is thus associated with the gravitational force only and mechanical energy of the system is conserved .
(i) Let potential energy of the system is conserved .
L=0
∴mgL=0
Total mechanical energy point A,
E=12mv20[∴Newton.s Second law]
E=12mv02 ....(1)
The velocity of bob at point A , is v0
Bob moving circular .
∴ Resultant force is string = centripetal force TA−mg=mv20L[∴Newton.s Second law]
Where TA is the tension in the string at A. At the highest point C, the string = centripetal force
TA−mg=mv20L[∴Newton.s Second Law]
Where TA is the tension in the tring at A. At the highest [point C, the string slackens , as the tension in the string TC become zero.
Thus , at C
E=12mv2C+2mgL ....(2)
Where TA is the tension in the string t A. At the highest point C, the string slackness, as the tension in the string TCbecomes zero. Thus at C
E=12mv2C+2mgL ...(2)
mv2CL=mg .Newton.s second law ]
Where vc is the speed at C
∴v2C=mgL ....(3)
And v2C−gL ...(4)
∴ From equation (2). ,
E=12mgL+2mL
∴E=5mgL2 ...(5)
12mv20=5mgL2 [ From equation (1)]
∴v0=√5gL ...(6)
(ii) From equation (4),
vC=√gL ...(7)
and at the Btotal mechanical energy .
E=12mv2B+mgL [∴h=L]
From equation (6) and (1),
12mv20=12mv2B+mgL
12m5gL=12mv2B+mgL
[∴From equation (7)]
∴12mv2B=52mgL−mgL
12mv2B=32mgL
∴vB=√3gL
(iii)The ratio of the kinetic energies at B and C is :
The ratio of the kinetic energies at B and C is :
KBKC=12mv2B12mv2C=v2bv2C
∴KBKC=3gLgL=3:1
At point C , the string becomes slack and the to the left . If the string is cut at this instant , the bob will execute a projectile to motion with horizontal and to the left . If the string is cit at this instant , the bob will execute a projectile to motion with horizontal projection akin to motion with horizontal projection akin to a rock kicked horizontally from the edge of a sliff. Otherwise the bob will continue on its circular pathand complete the revolution .
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - B Numericals (Numerical From Textual Exercise)
Explore 42 Videos
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - B Numericals (Numerical From .DARPAN. Based On Textbook)
Explore 15 Videos
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - A Questions - Answers (Try Yourself (VSQs))
Explore 74 Videos
- WAVESBook:KUMAR PRAKASHANChapter:WAVESExercise:SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
Explore 23 Videos
Similar Questions
The sign of work done by a force on a body is important to understand .State carefully if the following quantities are positive or negative :
(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket .
(b) work done by gravitational force in the above case ,
(c ) work done by friction on a body siding down an inclined plane ,
(d ) workdone by an applied force on a body moving on a rough horizontal plane woth uniform velocity .
(d) work done by the resistive force of air on a vibrating pendulum in bringing it to rest .
View SolutionA body while being acted upon by a force →F(x)=(3x2−2x+7)ˆi N gets displaced from x = 0 to x = 10 m in the direction of X -axis .Find the work done [∫xndx=xn+1n+1]
View SolutionDefine the scalar product of two vectors .
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
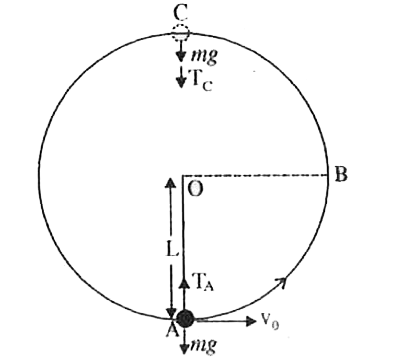
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
View SolutionA mass m is hanging by a string of length l. The velocity v0 which must be imparted to it to just reach the top is
View Solutionm द्रव्यमान का एक गोलक L लंबाई की हल्की दूरी से लटका हुआ है । इसके निम्नतम बिंदु A पर क्षैतिज वेग v0 इस प्रकार लगाया जाता है कि यह ऊर्ध्वाधर तल में अर्द्धवृत्ताकार प्रक्षेप्य पथ को इस प्रकार तय करता है कि दूरी केवल उच्चतम बिंदु C पर ढीली होती है , जैसा कि चित्र में दर्शाया गया है । निम्न राशियों के लिए व्यंजक प्राप्त कीजिए -
( a ) v0
( b ) बिंदुओं B तथा C पर गोलक की चाल तथा
( c ) बिंदु B तथा C पर गतिज ऊर्जाओं का अनुपात (KBKC)
गोलक के बिंदु C पर पहुँचने के बाद पथ की आकृति पर टिपण्णी कीजिये ।
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v_( 0) to complete the vertical circle. The tension in the string when it becomes horizontal is
View Solutionm द्रव्यमान का एक गोलक L लम्बाई की हल्की डोरी से लटका हुआ है। इसके निम्नतम बिंदु A पर क्षैतिज वेग v0 इस प्रकार लगाया जाता है की यह ऊर्ध्वाधर तल से अर्द्धवृत्ताकार प्रक्षेप्य पथ को इस प्रकार तय करता है की डोरी केवल उच्चतम बिंदु C पर ढीली होती है जैसा की चित्र में दिखाया गया है। निम्न राशियों के लिये व्यंजक प्राप्त कीजिये - (a ) v0 (b ) बिन्दुओ B तथा C पर गोलक की चाल तथा (c ) बिंदु B तथा C पर गतिज ऊर्जाओं का अनुपात (KBKC) गोलक के बिंदुC पर पहुँचने के बाद पथ की प्रकृति पर टिप्पणी कीजिये।
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
vo
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(o) at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for The speeds at points B and C.
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
The ratio of the kinetic energies (KB/KC) at B and C. Comment on the nature of the trajectory of the bob after it reaches the point C.
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
vo
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(o) at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for The speeds at points B and C.
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. Obtain an expression for
The ratio of the kinetic energies (KB/KC) at B and C.
View Solution

