m द्रव्यमान का एक गोलक L लम्बाई की हल्की डोरी से लटका हुआ है। इसके निम्नतम बिंदु A पर क्षैतिज वेग $v_{0}$ इस प्रकार लगाया जाता है की यह ऊर्ध्वाधर तल से अर्द्धवृत्ताकार प्रक्षेप्य पथ को इस प्रकार तय करता है की डोरी केवल उच्चतम बिंदु C पर ढीली होती है जैसा की चित्र में दिखाया गया है। निम्न राशियों के लिये व्यंजक प्राप्त कीजिये - (a ) $v_{0}$ (b ) बिन्दुओ B तथा C पर गोलक की चाल तथा (c ) बिंदु B तथा C पर गतिज ऊर्जाओं का अनुपात $(\frac{K_{B}}{K_{C}})$ गोलक के बिंदुC पर पहुँचने के बाद पथ की प्रकृति पर टिप्पणी कीजिये।

Video Solution

Text Solution

Verified by Experts

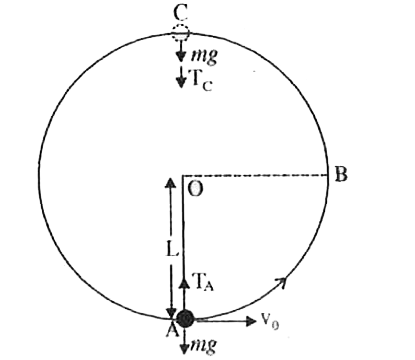
चित्र में गोलक पर लगने वाले दो बाह्य बल है गुरुत्व बल और डोरी में तनाव । बाद वाला बल कोई कार्य नहीं करता है , क्योंकि डोरी का विस्थापन हमेशा केवल गुरुत्वाकर्षण बल से सम्बंधित है। इस निकाय की सम्पूर्ण ऊर्जा E अचर है । बिंदु A पर स्थितिज ऊर्जा को शून्य लेते है ।
अतः बिंदु A पर यांत्रिक ऊर्जा
$E = \frac{1}{2} m v_{0}^{2}$ ....(1)
न्यूटन के गति के दूसरे नियम से
$T_{A} - m g = \frac{m v_{0}^{2}}{L}$
यहाँ $T_{A}$ बिंदु A पर डोरी का तनाव उच्चतम बिंदु C पर डोरी ढीली हो जाती है। यहाँ पर $T_{C} = 0$ अतः बिंदु C पर हमें प्राप्त होता है।
यांत्रिक ऊर्जा = गतिज ऊर्जा + स्थितिज ऊर्जा
$∴ E = \frac{1}{2} m v_{C}^{2} + m g \times (2 L)$ ......(2)
न्यूटन के द्वितीय नियमानुसार
$m g = \frac{m v_{C}^{2}}{L} ... . . (3)$
या $m g L = m v_{C}^{2} ∴ v_{C}^{2} = g L$
समीकरण (2 ) में मान रखने पर
$E = \frac{1}{2} \times m g L + 2 m g L = \frac{5}{2} m g L$ .... (4)
समीकरण (1 ) तथा (4 ) को बराबर करने पर
$\frac{5}{2} m g L = = \frac{m}{2} v_{0}^{2}$
अथवा $5 g L = v_{0}$
अथवा $v_{0} = \sqrt{5 g L}$
(b) अतः बिंदु B पर कूल ऊर्जा है।
$E = \frac{1}{2} m v_{B}^{2} + m g L$ .....(5)
इसे बिंदु A पर ऊर्जा के व्यंजक के बराबर रखने पर
$\frac{1}{2} m v_{B}^{2} + m g L = \frac{1}{2} m v_{0}^{2}$
या $v_{B}^{2} + 2 g L = 5 g L$
या $v_{B}^{2} = 5 g L - 2 g L = 3 g L$
$∴ v_{B} = \sqrt{3 g L}$
(c ) बिंदु व पर गतिज ऊर्जाओं का अनुपात
$\frac{K_{B}}{K_{C}} = \frac{\frac{1}{2} m v_{B}^{2}}{\frac{1}{2} m v_{C}^{2}}$
या $\frac{K_{B}}{K_{C}} = \frac{V_{B}^{2}}{v_{C}^{2}} = \frac{3 g L}{g L} = \frac{3}{1}$
बिंदु C पर डोरी ढीली हो जाती है और गोलक का वेग बाई और को एवं क्षैतिज हो जाता है । यदि इस क्षण पर डोरी को काट दिया जाए तो गोलक एक क्षैतिज प्रक्षेप की तरह प्रक्षेप्य गति ठीक उसी प्रकार दर्शायेगा जैसा की खड़ी चट्टान से क्षैतिज दिशा में किसी पत्थर फेंकने पर होता है। अन्यथा गोलक लगातार अपने वृत्ताकार पथ पर गति करता रहेगा और परिक्रमण को पूरा करेगा

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

SANJEEV PUBLICATION-कार्य ऊर्जा और शक्ति -गत वर्षो के विभिन्न प्रतियोगी परीक्षाओ में पूछे प्रश्न

Home
Ask Doubt
Profile