Consider the collision depicted in figure to be between two billiard balls are equal masses m1=m2 . The first ball is called the cue while the second ball is called the target . The billiard player wants to 'sink ' the target ball in a corner pocket , which is at angle θ2=37∘ .Assume that the collision is elastic and that friction and rotational motion are not important . Obtain θ1 .
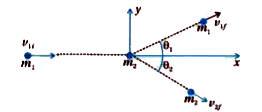 Solution in Gujrati
Solution in Gujrati
From the law of conservation of momentum ,
m1→vli=m2−→v2i=m1−→v1f+m2→v2f
but m1=m2and−→v2i=0
∴v2li=(−−→v1f+−→v2f).(−→v1f+−→v2f)
∴v2li=v21f+v22f+2−→v1f.−→v2f
∴v2li=v21f+2v1fv2fcos(θ+37∘)....(1).
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - B Numericals (Numerical From Textual Exercise)
Explore 42 Videos
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - B Numericals (Numerical From .DARPAN. Based On Textbook)
Explore 15 Videos
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - A Questions - Answers (Try Yourself (VSQs))
Explore 74 Videos
- WAVESBook:KUMAR PRAKASHANChapter:WAVESExercise:SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
Explore 23 Videos
Similar Questions
The sign of work done by a force on a body is important to understand .State carefully if the following quantities are positive or negative :
(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket .
(b) work done by gravitational force in the above case ,
(c ) work done by friction on a body siding down an inclined plane ,
(d ) workdone by an applied force on a body moving on a rough horizontal plane woth uniform velocity .
(d) work done by the resistive force of air on a vibrating pendulum in bringing it to rest .
View SolutionA body while being acted upon by a force →F(x)=(3x2−2x+7)ˆi N gets displaced from x = 0 to x = 10 m in the direction of X -axis .Find the work done [∫xndx=xn+1n+1]
View SolutionDefine the scalar product of two vectors .
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionTwo identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37^(@) with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View SolutionConsider the collision depicted in Figure, to be between two billiard balls with equal masses m_(1)=m_(2) . The first ball is called the cue and the second ball is called the target. The billiard player wants to sink the target ball in a corner pocket, which is at an angle theta_(2)=phi=37^(@) . Assume that the collision is elastic and that friction and rotational motion are not important. Obtain theta_(1)=theta .
View SolutionA billiard ball collides elastically with an identical stationary ball. The collision is not head on. Show that the directions of motion of the two balls are at right angles after the collision. Solve the problem in centre of mass frame as well as in lab frame.
View SolutionSuppose the picture 6.10 Equal mass of impact ballard depicted in (m_1=m_2) It is between two balls in which the first ball is called the cue and the second ball is called the target. Player to target ball theta _2=37^@ Wants to fall in a corner bag. Suppose here that the impact is elastic and the rotation speed is not significant. The angle thetha_1 Find out
View SolutionA billiard ball of mass M , moving with velocity v1 collides with another ball of the same mass but at rest . If the collision is elastic , the angle of divergence after the collision is
View SolutionA billiard ball of mass M , moving with velocity v1 collides with another ball of the same mass but at rest . If the collision is elastic , the angle of divergence after the collision is
View SolutionA ball of mass m_(1) is moving with velocity 3v. It collides head on elastically with a stationary ball of mass m_(2) . The velocity of both the balls become v after collision. Then the value of the ratio (m_(2))/( m_(1)) is
View Solutionमान लीजिये की चित्र में चित्रित संघट्ट बिलियर्ड की समान द्रव्यमान (m1=m2) वाली दो गेंदों के मध्य हुआ है जिसमे प्रथम गेंद क्यू ( डण्डा ) कहलाती है और द्वितीय गेंद ' लक्ष्य ' कहलाती है। खिलाड़ी लक्ष्य गेंद को θ2=37∘ के कोण पर कोने में लगी थैली में गिराना चाहता है यहाँ मान लीजिये की संघट्ट प्रत्यास्थ है तथा घर्षण और घूर्णन गति महत्वपूर्ण नहीं है कोण θ1 ज्ञात कीजिये ।
View SolutionA billiards player hits a stationary ball by an identical ball to pocket the target ball in a corner pocket that is at an angle of 35∘ with respect to the direction of motion of the first ball. Assuming the collision as elastic and that friction and rotational motion are not important, the angle made by the target ball with repect to the incoming ball is
View Solutionमान लीजिए की चित्र में चित्रित संघट्ट बिलियर्ड की समान द्रव्यमान (m1=m2) वाली दो गेंदों के मध्य हुआ है। जिसमे प्रथम गेंद क्यू (डण्डा) कहलाती है और द्वितीय गेंद 'लक्ष्य' कहलाती है। खिलाडी लक्ष्य गेंद को θ2=37∘ के कोण पर कोने में लगी थैली में गिरना चाहता है। यहाँ मान लीजिए कि संघट्ट प्रत्यास्थ है तथा घर्षण और घूर्णन गति महत्त्वपूर्ण नहीं है। कोण θ1 ज्ञात कीजिए।
View SolutionConsider the collision depicted in Fig. 6.10. to be between two billiard balls with equal masses m1=m2. The first ball is called the cue while the second ball is called the target. The billiard player wants to 'sink' the target ball in a corner pocket, which is at an angle θ2=37∘. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain θ1.
View Solution

