A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
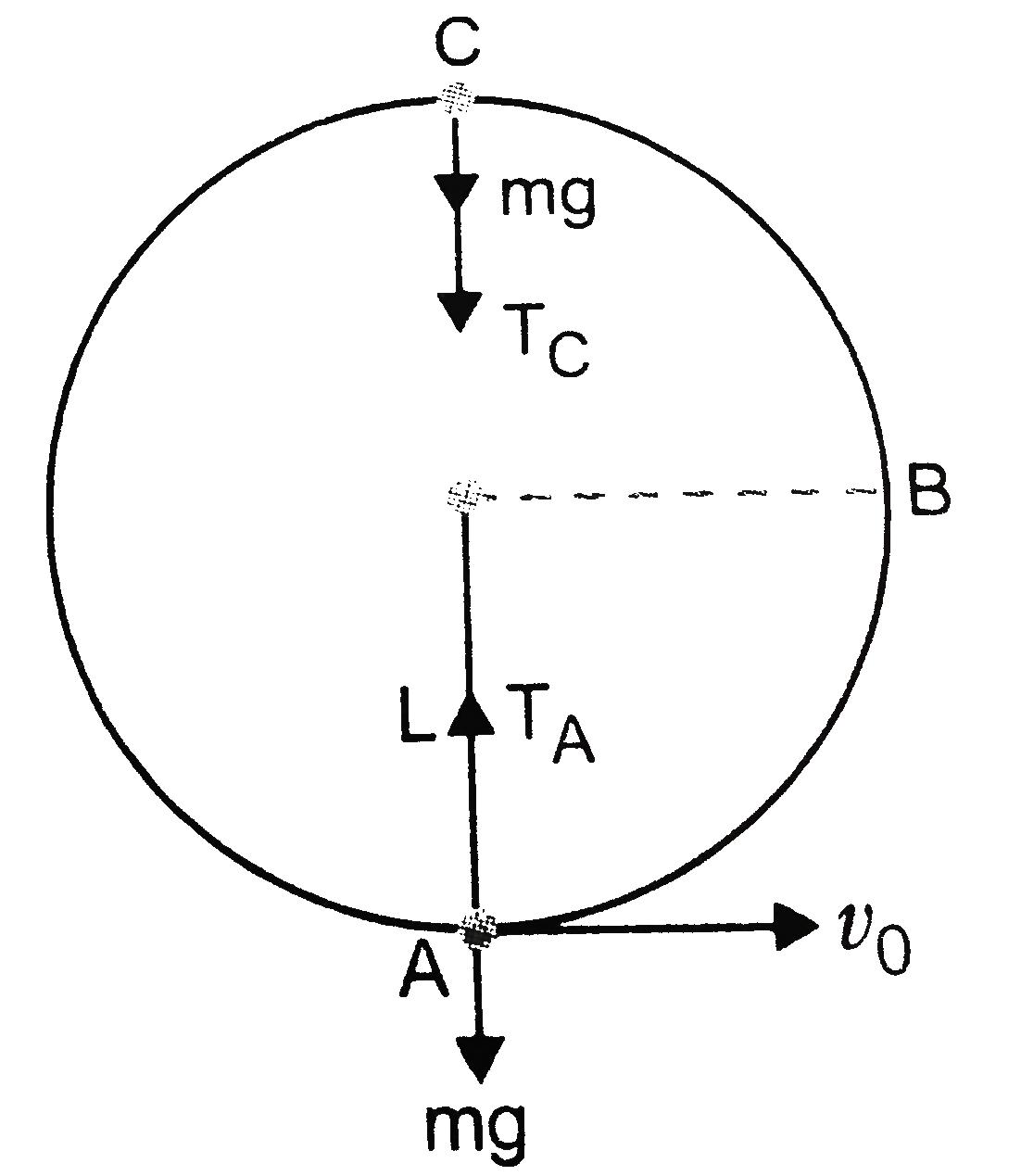
There are two external forces on the bob : gravity (mg) and tension (T) in the string. The tension does no work as displacement is always perpendicular to the string. Total mechanical energy (E) of the system is conserved.
If we take P.E. of the system to be zero at the lowest point A, then
At A, E=12mv20 ...(i)
The necessary centripetal force mv20/L is provided by (TA−mg).
TA−mg=mv20L ...(ii)
At the highest point C, the string slackens as the tension in the string (Tc) becomes zero.
∴ At C, mg=mv2CL ...(iii)
and total energy, E=12mv2C+mg(2L) ...(iv)
From (iii), vC=√gL ...(v)
From (iv), E=12m(gL)+2mgL=52mgL
Using (i), 12mv20=52mgL,v0=√5gL ...(vi)
At B, the energy is E=12mv2B+mg(L)
or 12mv2B=E−mg(L)=52mgL−mgL
=32mgL
vB=√3gL
KBKC=12mv2B12mv2C=3gLgL=31
At C, the string becomes slack and the velocity of the bob is horizontal and to the left. Therefore, the bob will continue on its circular path and complete the revolution.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems
27 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.
54 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A bob of mass ma suspended by a massle3ss inextensible string is rotated in a vertical circle of radius r as shoen in the figure. Obtain an expenssion for speeds and kinetic energies at A, B and C, Comment on the nature of trajectory of the bob after it reaches the point C.

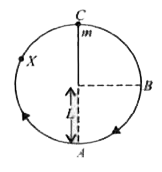
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure. What will be X the trajectory of the particle if the string is cut at
(a) Point B
(b) Point C
(c) Point X
View Solution
Knowledge Check
A bob of mas M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies.
 .Aθ=π4Bπ4<θ<π2Cπ2<θ<3π4D3π4<θ<π
.Aθ=π4Bπ4<θ<π2Cπ2<θ<3π4D3π4<θ<πA mass m is hanging by a string of length l. The velocity v0 which must be imparted to it to just reach the top is
A√3glB√4glC√5glD√6glThe bob of a simple prendulum is suspended by a strinng of length 80 cm . What minimum horizontal velocity should be imparted to the bob so that it reaches it reaches the height of suspension point ? (g=10m/s2)
A3m/sB4m/sC2m/sD5m/s
A body is suspended by a string of length l is projected with horizontal velocity V such that it does not complete the motion in vertical circles.Then the height at which tension becomes is zero is given by?
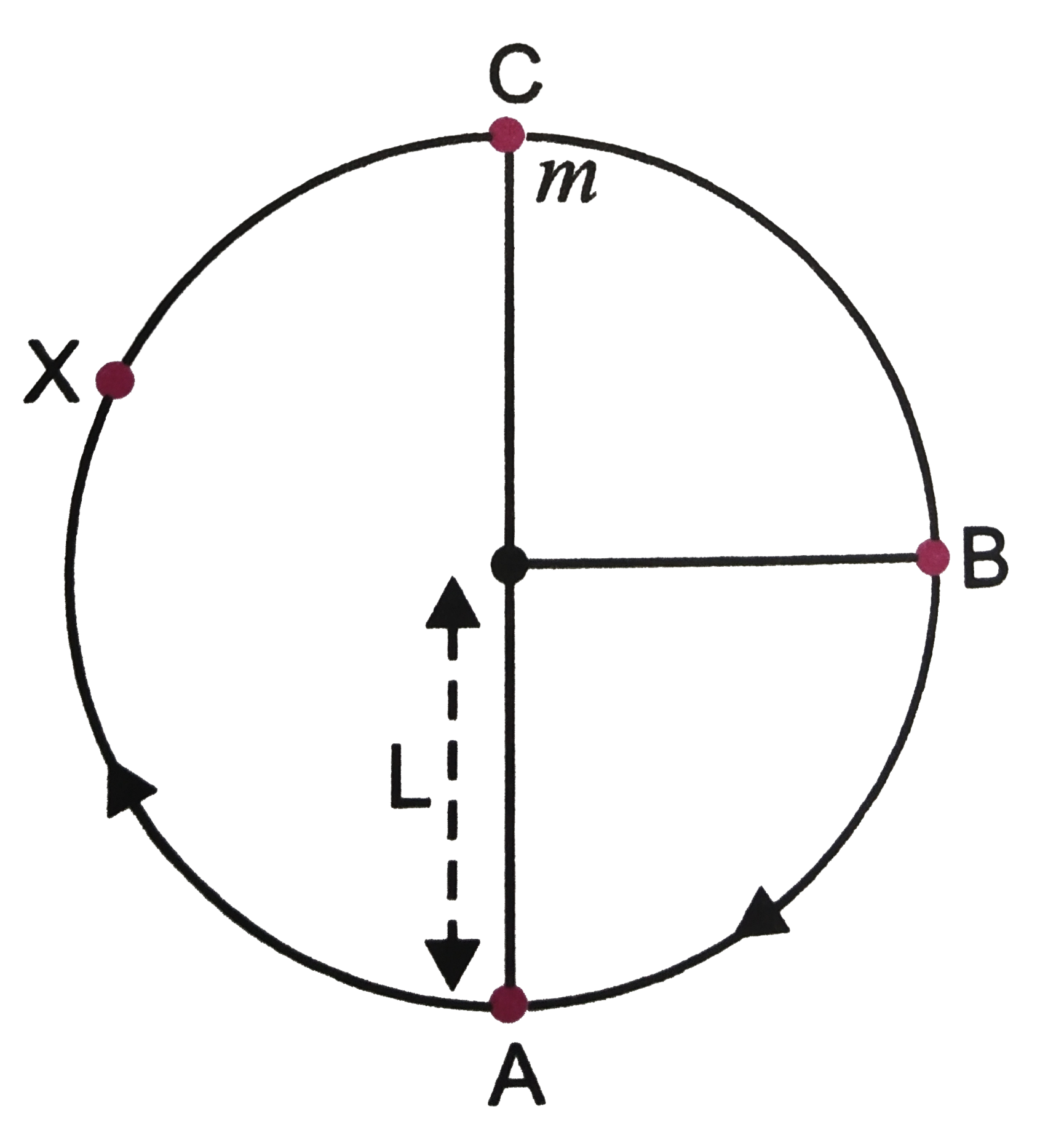
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
View SolutionA weight is suspended from a thread of length l. What is the initial speed that has to be imparted to it at the lowest point to make it complete a full revolution? The mass of the thread is to be neglected.
View SolutionA heavy particle hangs from a point O, by a string of length a. It is projected horizontally with a velocity u=√(2+√3)ag . The angle with the downward vertical, string makes where string becomes slack is :
View SolutionThe maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
View Solution
