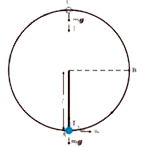
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
 Solution in Kannada
Solution in Kannada
There are two external forces on the bob : gravity and the tension (T) in the string. The latter does no work since the displacement of the bob is always normal to the string. The potential energy of the bob is thus associated with the gravitational force only. The total mechanical energy E of the system is conserved. We take the potential energy of the system to be zero at the lowest point A. Thus, at A ,
[Newton.s Second Law]
where is the tension in the string at A. At the highest point C, the string slackens, as the tension in the string becomes zero.
Thus, at C
[Newton.s Second Law] (6.14)
where is the speed at C. From Eqs. (6.13) and (6.14)
Equatting this to the energy at A
or, .
Similar Questions
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(o) at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for v_(o)
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
The speeds at points B and C.
 View Solution
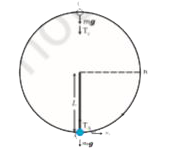
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(o) at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for The ratio of the kinetic energies (K_(B)"/"K_(C )) at B and C. Comment on the nature of the trajectory of the bob after it reaches the point C.
View SolutionA bob of mass m is suspeded by a light string of length L . It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semicircular trajectroy in the vertical plane with the string becoming slack only on reaching the topmost point C . Thisis shown in figure .Obtain a expression for (i) v0 (ii) the ratio of the kinetic energies (KBKC) at B and C . Comment on the nature of the trajectroy of the bob after it reaches the point C .
 08:09View Solution
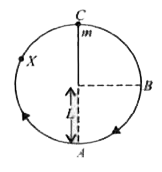
08:09View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown figure . What will be the trajectory of the particle , if the string is cut at (a) point B ? (b) point C ? (C ) Point X ?
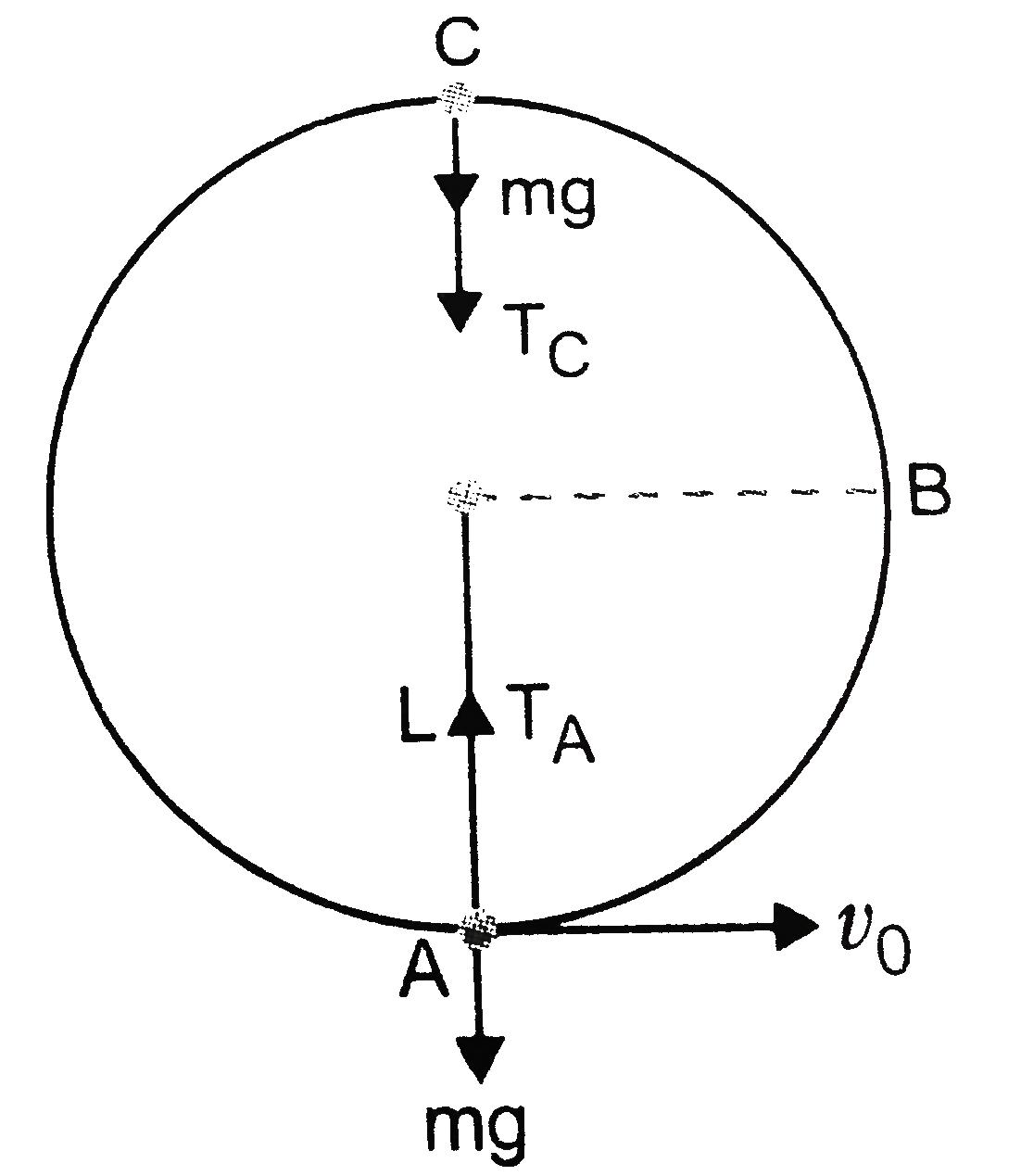
05:51View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
 08:32View Solution
08:32View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure. What will be X the trajectory of the particle if the string is cut at
(a) Point B
(b) Point C
(c) Point X
 View Solution
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v_(0) at the lowest point A such that it completes a semicircular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C this is shown in Fig. Obtain an expression for v_(o)
04:15View Solution
