A narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen ∑ placed at a distance LD from the slit. a. What will be the intensity at a point just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
?
The correct Answer is:A, B, D
a. Since there is a phase difference of π between direct light and reflecting light the intensity just above the mirror will be zero.ltbr> B. Here 2nd= equivalent slit seperationn
D=distance between slit and screen.
We know for bright fringe
△x=y×2dD=nλ
But as thereis a phase reversal of λ2
→(y×2d)D=λ2=nλ
→y×2dD=nλ=λ2(n−12)=λ2
→y=λD4D
Topper's Solved these Questions
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -2
10 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
Similar Questions
A narrow slit S transmitting light of wavelength 'λ'. Is placed at a distance d above a large plane mirror as shown. The light coming directly from the slit and that coming after the reflection interfere at a screen S placed at a distance D from the slit. at what distance from point O, the resultant intensity is maximum ? (there is a phase change of π of reflection from the mirror)
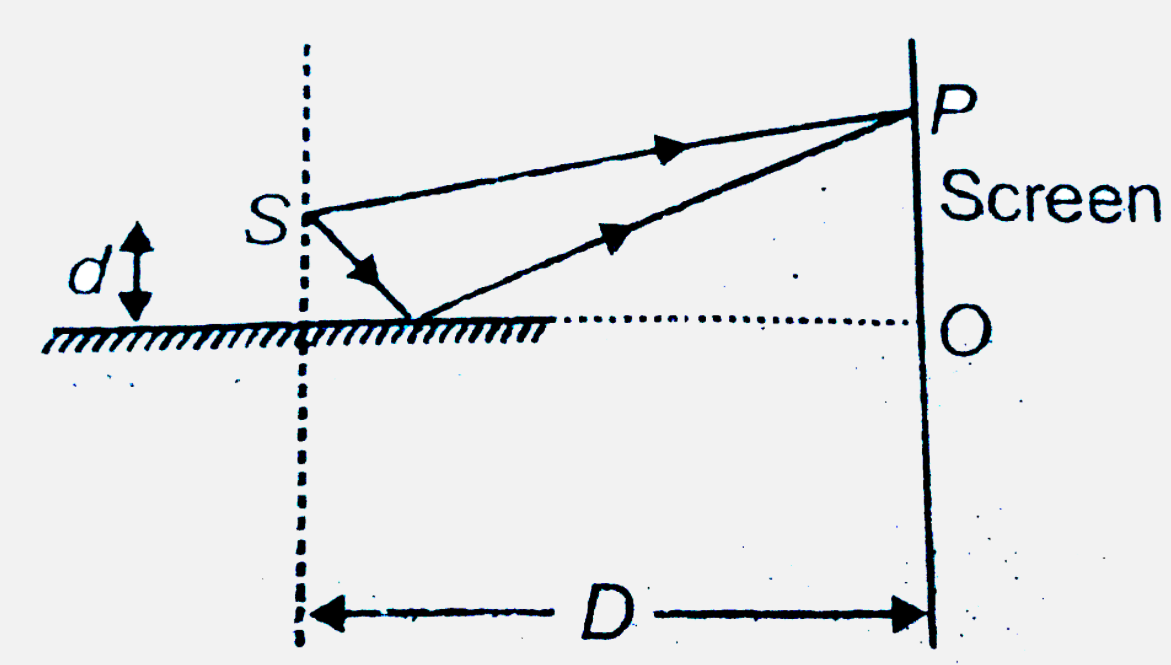
View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?
View Solution
Knowledge Check
In a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
AdλBλ2dDCD22λDDd22Dλ
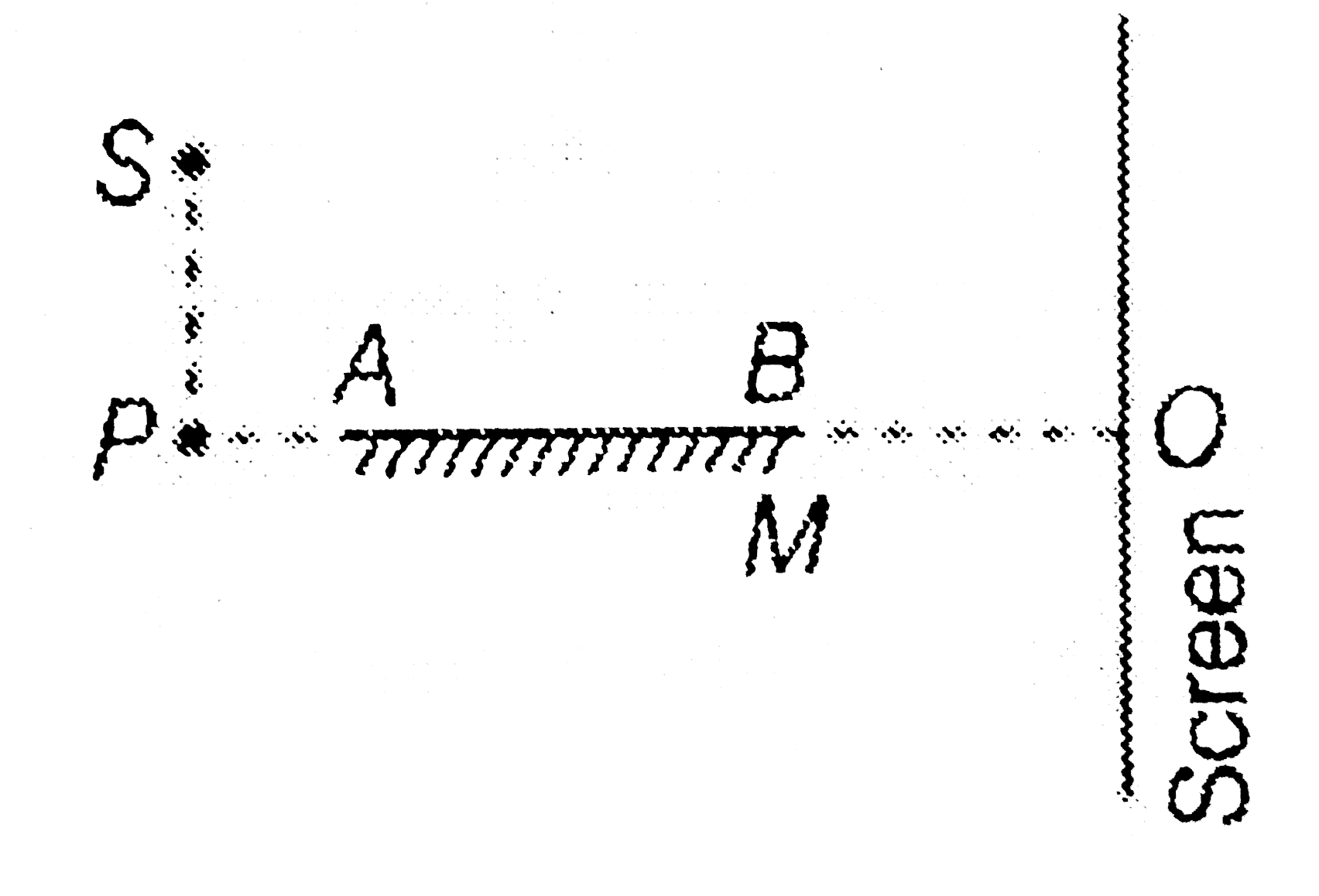
A long narrow horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit, Find the fringe-width if the light used has a wavelength of 700 nm.
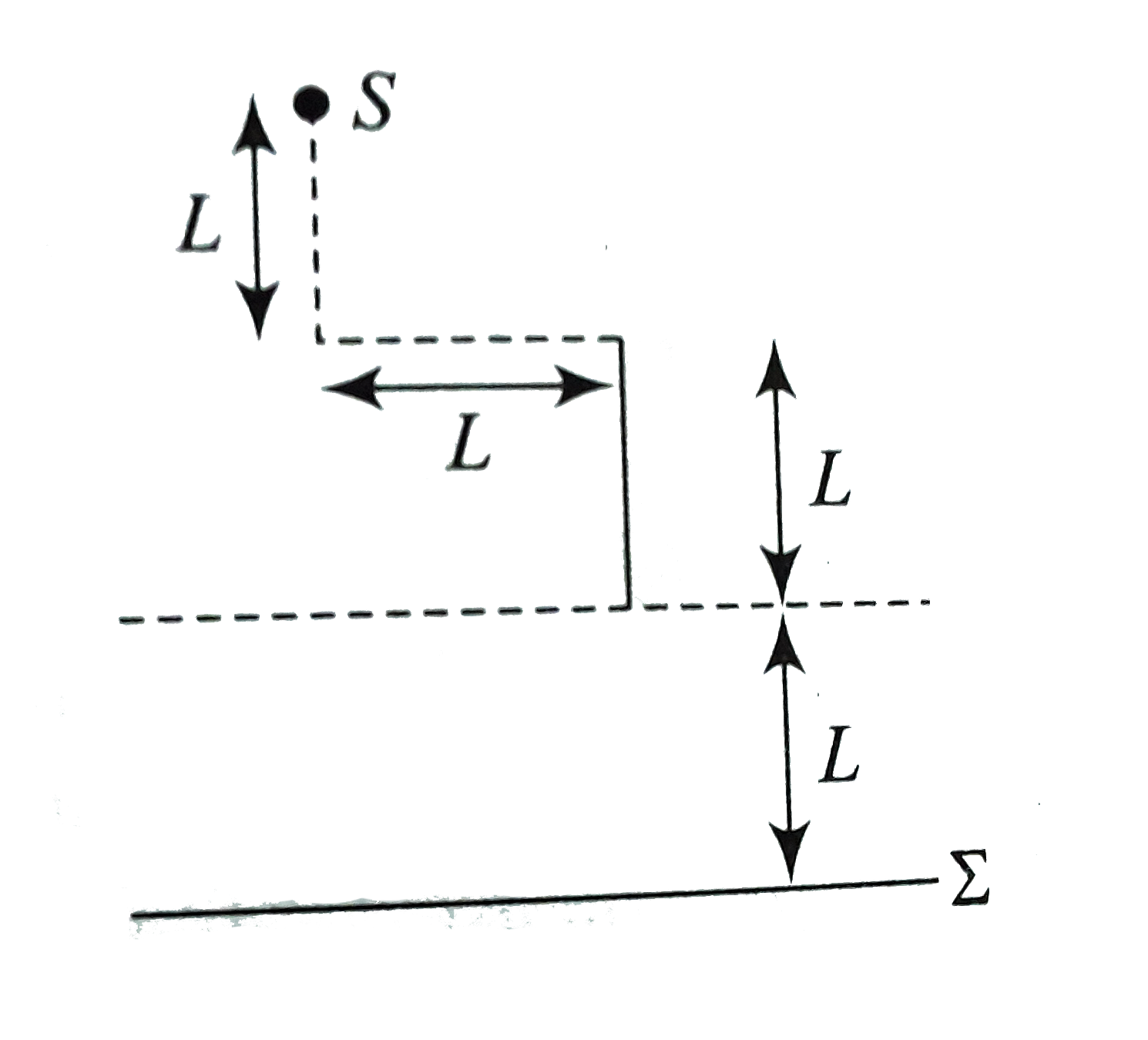
View SolutionA point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen Σ
View SolutionA long horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and the after reflection is seen on a screen 1 m away from the slit. If the mirror reflects only 64% of the light falling on it, the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen is
View SolutionA long narrow horizontal slit lies 1mm above a plane mirror. The interference pattern produced by the slit and its and its image is viewed on a screen ∑ distance 1m from the slit. The wavelength of light is 600nm. Then the distance of the first maxima above the mirror is equal to (d<<D) :

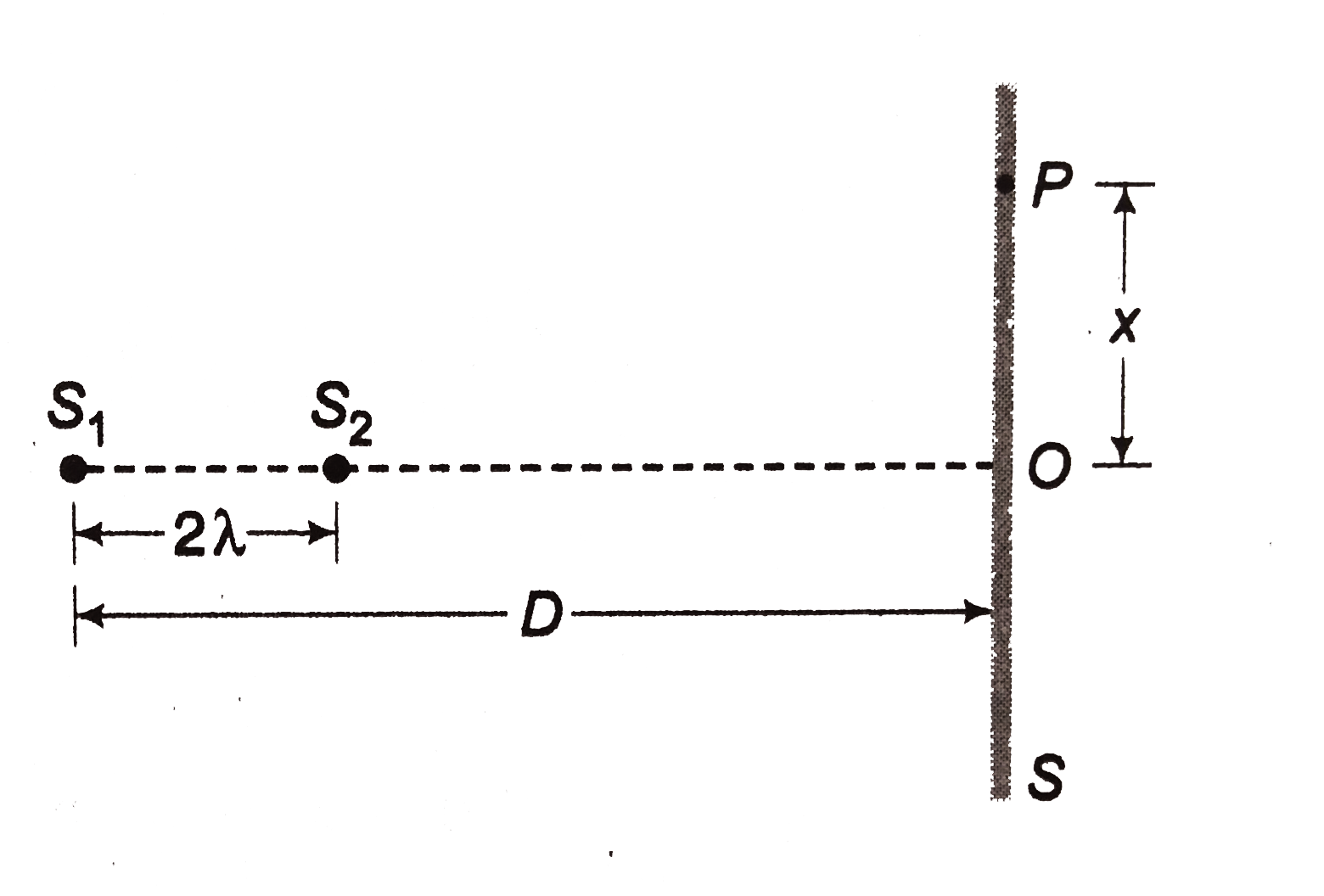
View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
 .
.
View SolutionA double slit S1−S2 is illuminated by a coherent light of wavelength λ. The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1, from it and a screen ∑ is placed behind the double slit at a distance D2, from it . The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
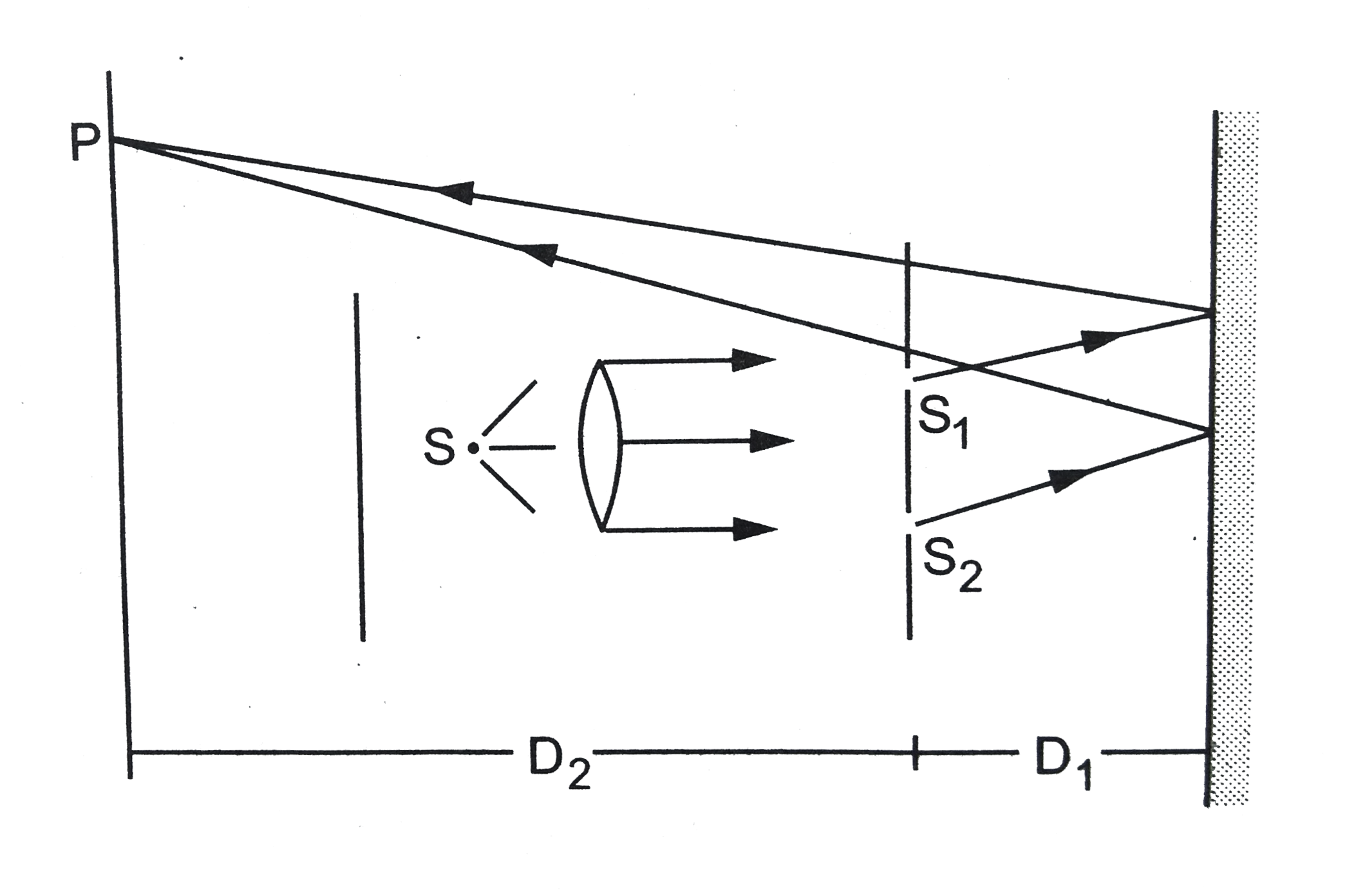
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
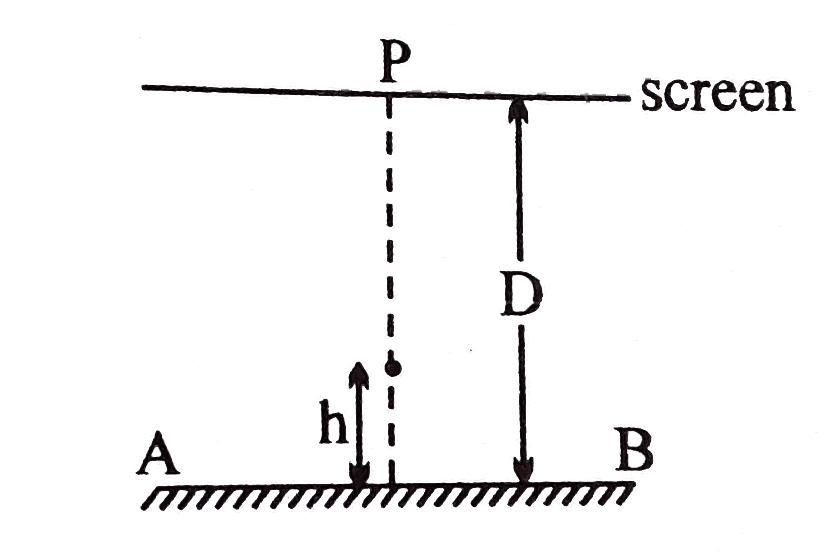
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
View Solution
