A long horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and the after reflection is seen on a screen 1 m away from the slit. If the mirror reflects only 64% of the light falling on it, the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen is
8:1
3:1
81:1
9:1
The correct Answer is:c
To solve the problem, we will follow these steps:
Step 1: Define the intensities
Let the intensity of the light from the slit be I1. The intensity of the light after reflection from the mirror, which reflects 64% of the light, will be:
I2=0.64I1
Step 2: Relate intensities to amplitudes
Since intensity is proportional to the square of the amplitude, we can express the relationship between the amplitudes A1 and A2 as follows:
I2I1=A22A21
Substituting for I2:
0.64I1I1=A22A21
This simplifies to:
A22A21=0.64
Taking the square root gives:
A2A1=√0.64=45
Step 3: Calculate maximum and minimum intensities
The maximum intensity Imax and minimum intensity Imin in the interference pattern can be calculated using the amplitudes:
Imax=(A1+A2)2
Imin=(A1−A2)2
Substituting A2=45A1:
Imax=(A1+45A1)2=(95A1)2=8125A21
Imin=(A1−45A1)2=(15A1)2=125A21
Step 4: Find the ratio of maximum to minimum intensity
Now, we can find the ratio of maximum to minimum intensity:
ImaxImin=8125A21125A21=811=81
Conclusion
Thus, the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen is:
81
Let the intensity of the light from the slit be I1. The intensity of the light after reflection from the mirror, which reflects 64% of the light, will be:
I2=0.64I1
Since intensity is proportional to the square of the amplitude, we can express the relationship between the amplitudes A1 and A2 as follows:
I2I1=A22A21
Substituting for I2:
0.64I1I1=A22A21
This simplifies to:
A22A21=0.64
Taking the square root gives:
A2A1=√0.64=45
The maximum intensity Imax and minimum intensity Imin in the interference pattern can be calculated using the amplitudes:
Imax=(A1+A2)2
Imin=(A1−A2)2
Imax=(A1+45A1)2=(95A1)2=8125A21
Imin=(A1−45A1)2=(15A1)2=125A21
Now, we can find the ratio of maximum to minimum intensity:
ImaxImin=8125A21125A21=811=81
Thus, the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen is:
81
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective11videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
A long narrow horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit, Find the fringe-width if the light used has a wavelength of 700 nm.
View SolutionConsider the situation of the previous problem, if the mirror reflects only 64% of the light energy falling on it, what will be the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen ?
View Solution
Knowledge Check
- Question 1 - Select One
The intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
A2:1B34:1C9:1D8:1
The intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
View SolutionA long narrow horizontal slit lies 1mm above a plane mirror. The interference pattern produced by the slit and its and its image is viewed on a screen ∑ distance 1m from the slit. The wavelength of light is 600nm. Then the distance of the first maxima above the mirror is equal to (d<<D) :
 View Solution
View SolutionThe width of one of the two slits in a Young's double slit experiment is double of the other slit. Assuming that the amplitude of the light coming from a slit is proportional to the slit width, find the ratio of the maximum to the minimum intensity in the interference pattern.
View SolutionThe width of one of the two slits in a Young's double slit experiment is double of the other slit. Assuming that the amplitude of the light coming from a slit is proportional to the slit width, find the ratio of the maximum to the minimum intensity in the interference pattern.
View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
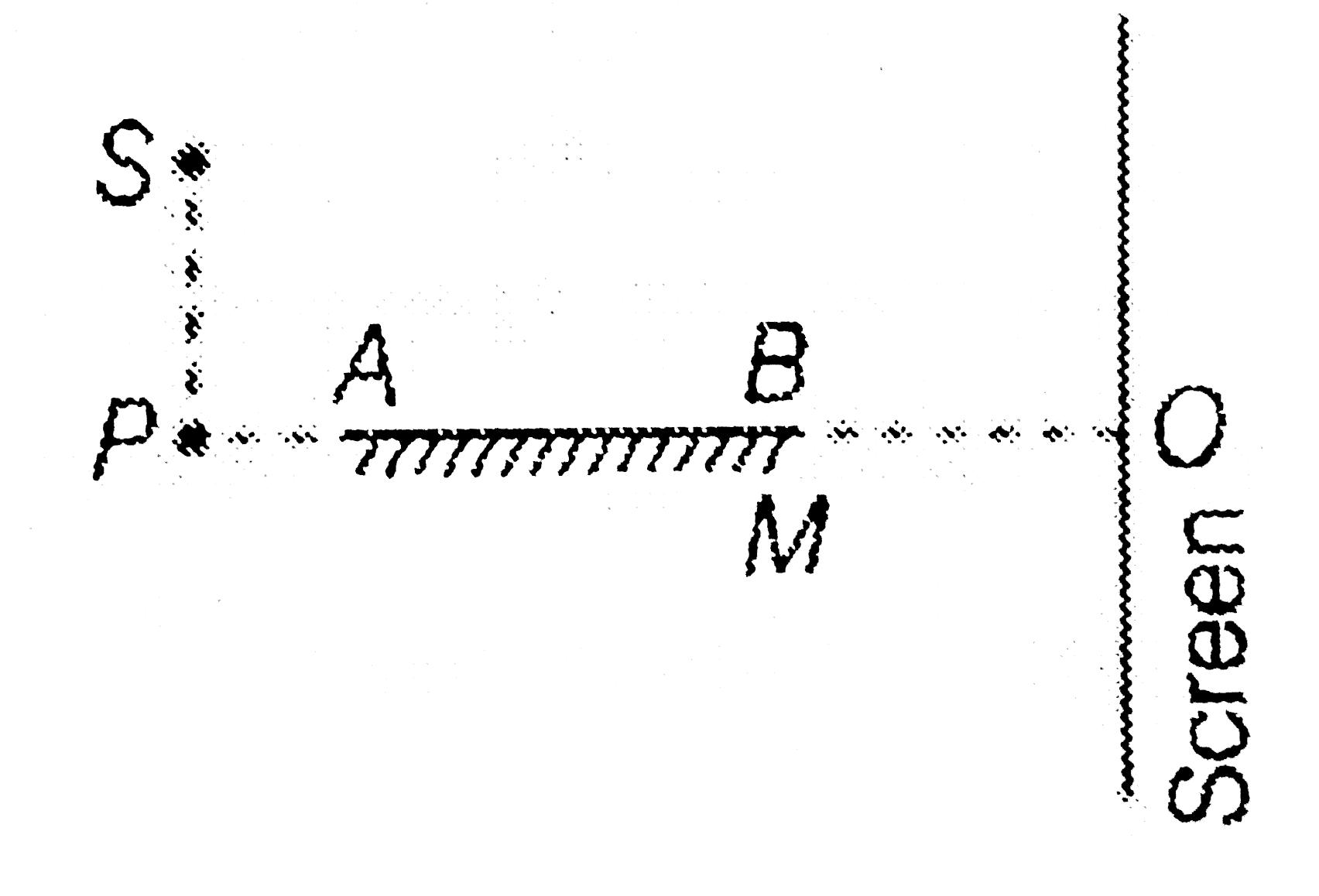
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?View SolutionA narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen ∑ placed at a distance LD from the slit. a. What will be the intensity at a point just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
? View Solution
View SolutionThe intensity of light emerging from one slit is nine times than that from the other slit in Young's double sit interference set up. The ratio of maximum intensity to minimum intensity in the fringe pattern is
View Solution
