A point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
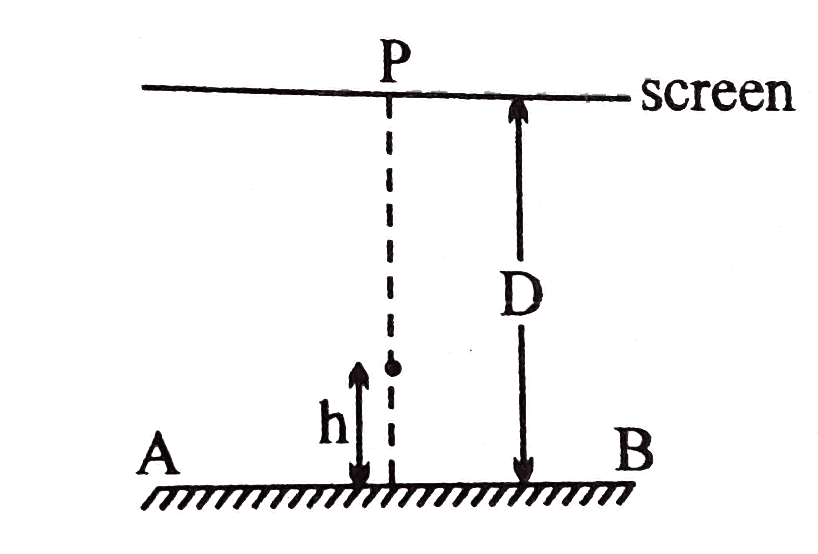
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
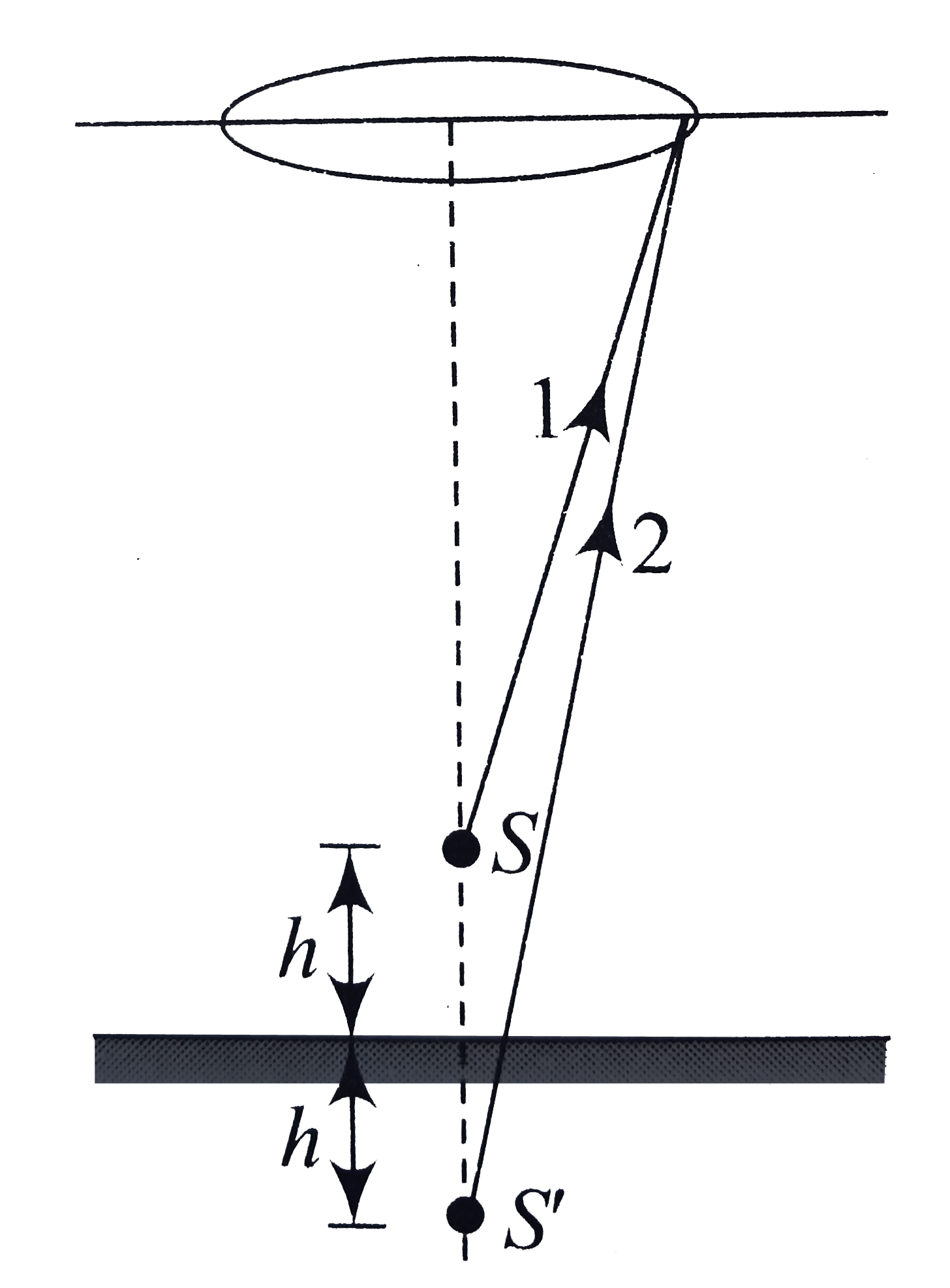
a. The path difference between the rays 1 and 2 coming from S and S' will be equal on the circular path on the screen, hence fringes will be circular.
Let the intensity of light coming from S be I1=I, then as per the problem, the velocity of the reflected light will be I2=0.36I.
As we know
Imax=(√I1+√I2)2
Imin=(√I1−√I2)2
Hence, ImaxImin=(√I1+√I2)2(√I1−√I2)2
=(√I+√0.36I)2(√I−√0.36I)2=116
To have the next maximum at P, the path difference between the interfering waves must change by λ. If AB is moved by a distance x, it will cause an additional path difference 2x
2x=λ (value minimum value of x)
⇒x=λ2=300mm
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
A point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. If the intensity of P correspoonds to a maximum, calculate the minimum distance through which the reflecting surface AB should so that intensity at P again becomes maximum.

View SolutionA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. What is the shape of interference fringes on the screen?

View Solution
Knowledge Check
The intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
A2:1B34:1C9:1D8:1
A point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. What is the percentage intensity of the reflected light to the intensity of the reflectd light to the intensity of incident light?

View SolutionIf S1andS2 are two point sources emitting light in phase , then what is the shape of interference fringes formed on the screen ?
View SolutionShape of interference fringes formed on the screen due to point source P, in the case shown here

View SolutionConsider the situation of the previous problem, if the mirror reflects only 64% of the light energy falling on it, what will be the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen ?
View SolutionThe intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
View SolutionA particle is placed on the top of a hemispherical shell of same mass. Shell is free to move on the smooth ground. If particle is given a given a gentle push and reaches to angular position q as shown in figure then for an observer fixed on a shell, ratio of reaction force exerted by shell to pseudo force (as observed from shell) acting on particle, is

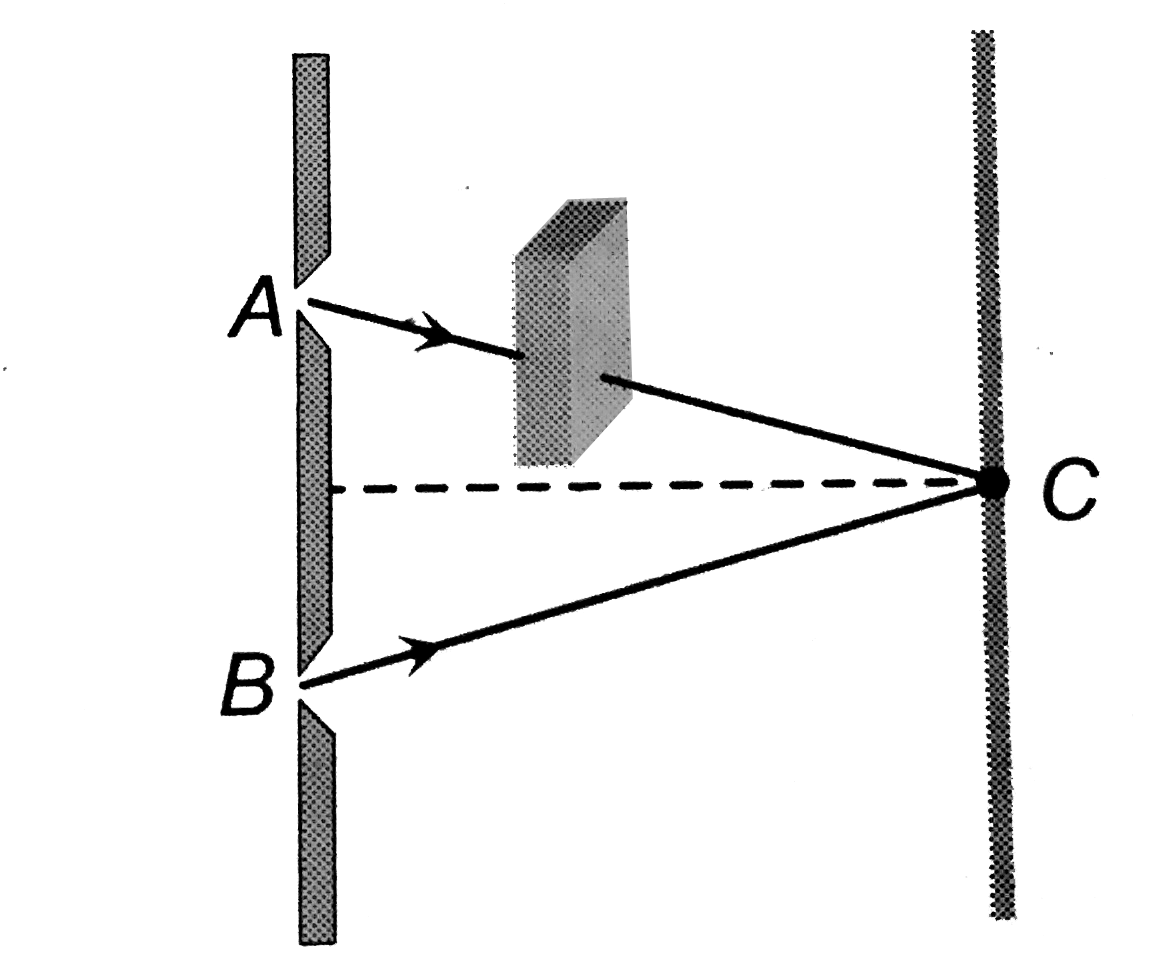
View SolutionIn Young's experiment, monochromatic light is used to illuminate the two slits A and B. Interference fringes are observed on a screen placed in front of the slits. Now if a thin glass plate is placed normally in the path of the beam coming from the slit
View Solution
