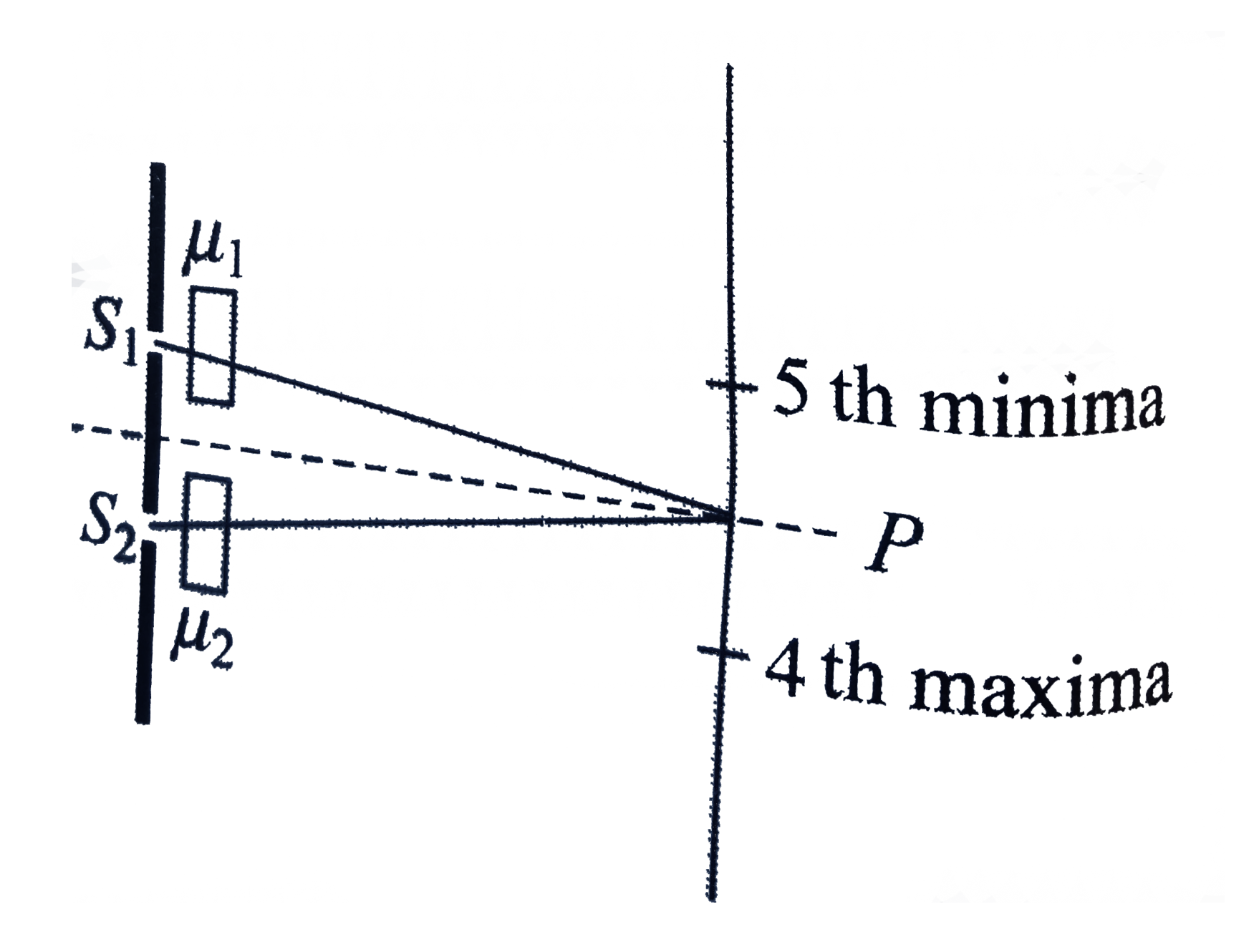
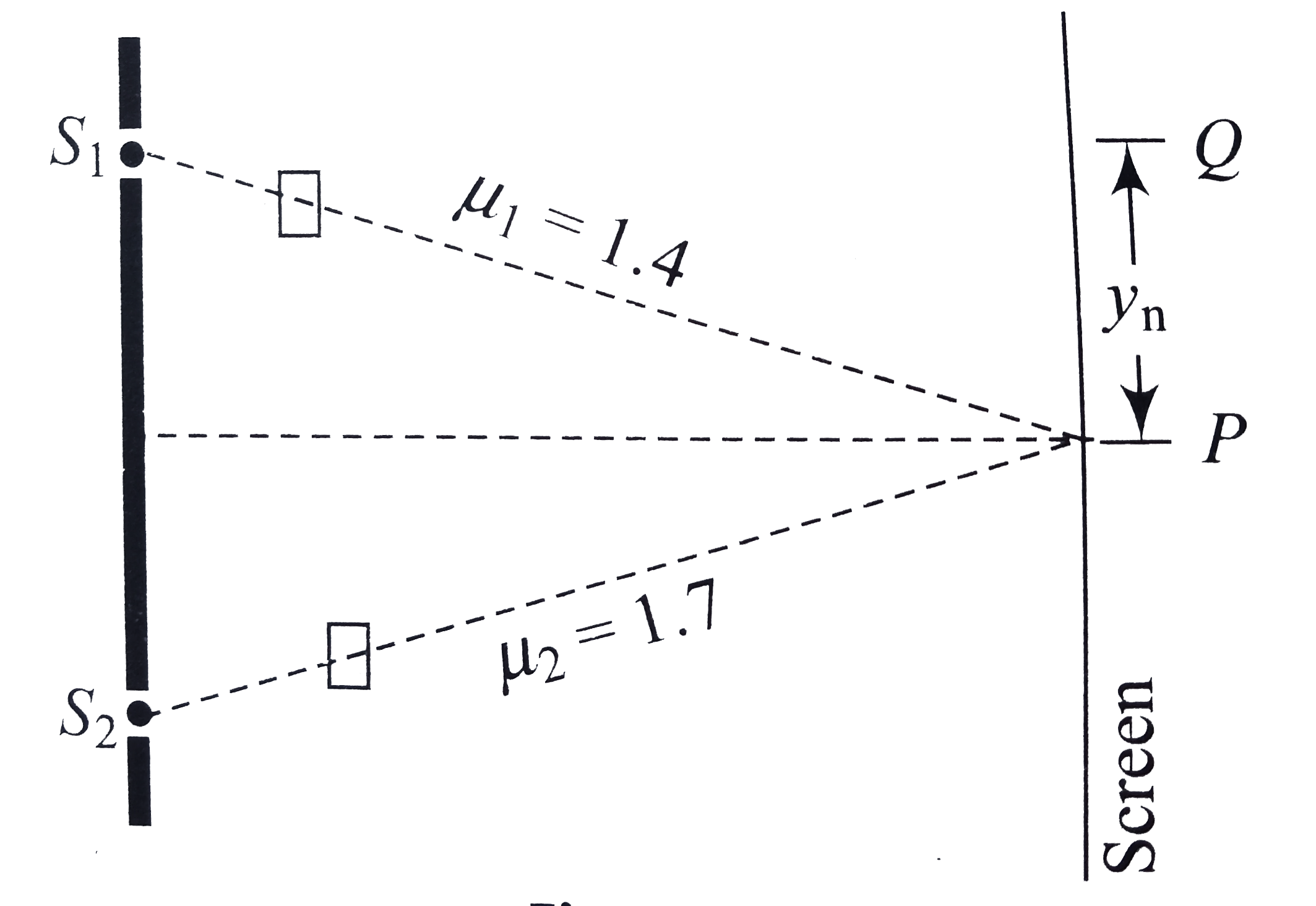
In Young's experiment the upper slit is covered by a thin glass plate of refractive index $1.4$ while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index $1.7$ interference pattern is observed using light of wavelength $5400 Å$
It is found that point P on the screen where the central maximum $(n = 0)$ fell before the glass plates were inserted now has $3 / 4$ the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
$In Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400 Å It is found that point P on the screen where the central maximum (n = 0) fell before the glass plates were inserted now has 3//4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P. Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected. .$ .

Video Solution

Text Solution

Verified by Experts

Path difference between two waves starting from $S_{1}$ and $S_{2}$ and reaching at P,
$Δ = (μ_{2} - μ_{1}) t$ In the absence of plate, phase difference between two waves reaching at P equals zero. When the plates are introduced, let the phase difference between waves at P be $δ$ .
As the waves are of point of equal amplitude (or intensity), so initial intensity at P,
$I_{0} = {(a_{1} + a_{2})}_{1}^{2} = 4 a^{2}$
New intensity at P is
$I_{0} = {(a_{1} + a_{2})}_{1}^{2} = {(2 a)}^{2} = 4 a^{2}$
New Intensity at P is
$I = \frac{3}{4} I_{0} = \frac{3}{4} \times 4 a^{2} = 3 a^{2}$
We have,
$I = a_{1}^{2} + a_{2}^{2} + 2 a_{1} a_{2} cos δ$
$\Rightarrow 3 a^{2} = a^{2} + a^{2} + 2 a^{2} cos δ$
This gives
$δ = \frac{π}{3}, \frac{5 π}{3}, \frac{7 π}{3}, ... = (2 m π \pm \frac{π}{3}), m = 1, 2, 3, ...$
shift of interference pattern upward due to glass plate,
$1 = \frac{D}{d} (μ_{1} - 1) t = \frac{D}{d} (1.7 - 1) t$
Net shift downward is
$\frac{D}{d} (μ_{2} - μ_{1} t) = \frac{D}{d} (1.7 - 1.4) t = \frac{D}{d} (0.3 t)$
From given conditions,
$\frac{D}{d} (0.3 t) > \frac{5 λ D}{d}$ and $\frac{D}{d} (0.3 t) < (6 - \frac{1}{2}) \frac{λ}{d}$
$\Rightarrow \frac{5 λ}{0.3} < t < \frac{11 λ}{2 \times 0.3}$
$λ 5400 Å = 5.4 \times 10^{- 7} m$
Path difference created at P due to both the plates is $(μ_{2} - (μ_{1}) t$ .
Also, path difference,
$Δ = \frac{λ}{2 π} \times$ phase difference
$\Rightarrow (μ_{2} - μ_{1}) t = \frac{λ}{2 π} δ$
or $0.3 t = \frac{λ}{2 π} \times (2 m π \pm \frac{π}{3})$
= $(m \pm \frac{1}{6}) λ$
$= (m \pm \frac{1}{6}) \times 5.4 \times 10^{- 7} m$
From Eqs. (ii) and (iii), we have (putting m = 5),
$t = \frac{(5 + \frac{1}{6}) \times 5.4 \times 10^{- 7}}{0.3}$
$= 93 \times 10^{- 7}$ m taking $(+)$ sign
$= 87 \times 10^{- 7}$ m taking $(-)$ sign
In view of Eq. (ii),
$t = 93 \times 10^{- 7} m = 9.3 \times 10^{- 6} m = 9.3 μ m$

Updated on:21/07/2023

|

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-WAVE OPTICS-Solved Examples

Home
Ask Doubt
Profile