Answer the following:
(a) State Gauss' law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
let the field lines must be radically outward. Draw a cylinderical gaussian surface of radius r and length l. then, applying gauss' theorem
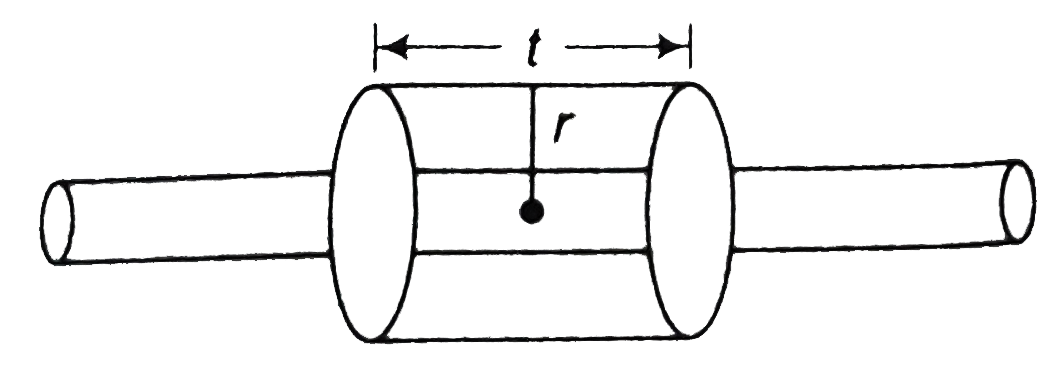
∫E.dS=1ε0λl
or Er2πrl=1ε0λl⇒Er=λ2πε0r
Hence, if r0 is the radius, V(r)−V(r0)=−∫rr0E.dl=λ2πε0ln(r0)r
Since, ∫rr0λ2πε0rdr=λ2πε0∫rr0dr=λ2πε0ln(r)r0
For a given V,
ln(r)r0=−2πε0λ[V(r)−V(r0)]
⇒r=r0e−2πε0Vr0/λe+2πε0V(r)/λ
r=r0e−2πε0[V(r)−V(r0)]/λ.
The equipotential surfaces are cylinders. of radius.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Short Answer Type Question
Explore 5 Videos
- ELECTROMAGNETIC WAVESBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:LONG ANSWER
Explore 5 Videos
- MAGNETISM AND MATTER Book:NCERT EXEMPLAR ENGLISHChapter:MAGNETISM AND MATTER Exercise:All Questions
Explore 24 Videos
Similar Questions
Answer the following:
State Gauss' law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.
View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionIf linear charge density of a wire as shown in the figure is λ

View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionFind the electric field at point O, due to the segment of a ring, whose linear charge density is 8C/cm

View Solution

