Prove that a closed equipotenitial surface with no charge within itself must enclose an equipotential volume.
To prove that a closed equipotential surface with no charge within itself must enclose an equipotential volume, we can follow these steps:
1. Understanding Equipotential Surfaces:
- An equipotential surface is defined as a surface where the electric potential is the same at every point.
2. Consider a Closed Equipotential Surface:
- Let’s denote our closed equipotential surface as S with a potential V. Since it is an equipotential surface, the potential is constant across the entire surface.
3. Apply Gauss's Law:
- According to Gauss's Law, the electric field E through a closed surface is given by:
∮E⋅dA=Qencϵ0
- Here, Qenc is the total charge enclosed by the surface S, and ϵ0 is the permittivity of free space.
4. No Charge Within the Surface:
- Since it is given that there is no charge within the surface, we have:
Qenc=0
- Therefore, by Gauss's Law, we can conclude:
∮E⋅dA=0
5. Implication for Electric Field:
- If the total electric flux through the surface is zero, it implies that the electric field E must be zero at every point inside the closed surface S. This is because if there were any electric field present, it would create a non-zero flux.
6. Relating Electric Field to Potential:
- The electric field is related to the electric potential V by the equation:
E=−dVdr
- Since we established that E=0 inside the surface, we can substitute this into the equation:
−dVdr=0
- This implies that dVdr=0, which means that the potential V is constant throughout the volume enclosed by the surface.
7. Conclusion:
- Since the potential V is constant throughout the volume enclosed by the surface S, we can conclude that the volume is indeed an equipotential volume.
Final Statement:
Thus, we have proved that a closed equipotential surface with no charge within itself must enclose an equipotential volume.
---
- An equipotential surface is defined as a surface where the electric potential is the same at every point.
- Let’s denote our closed equipotential surface as S with a potential V. Since it is an equipotential surface, the potential is constant across the entire surface.
- According to Gauss's Law, the electric field E through a closed surface is given by:
∮E⋅dA=Qencϵ0
- Here, Qenc is the total charge enclosed by the surface S, and ϵ0 is the permittivity of free space.
- Since it is given that there is no charge within the surface, we have:
Qenc=0
- Therefore, by Gauss's Law, we can conclude:
∮E⋅dA=0
- If the total electric flux through the surface is zero, it implies that the electric field E must be zero at every point inside the closed surface S. This is because if there were any electric field present, it would create a non-zero flux.
- The electric field is related to the electric potential V by the equation:
E=−dVdr
- Since we established that E=0 inside the surface, we can substitute this into the equation:
−dVdr=0
- This implies that dVdr=0, which means that the potential V is constant throughout the volume enclosed by the surface.
- Since the potential V is constant throughout the volume enclosed by the surface S, we can conclude that the volume is indeed an equipotential volume.
Thus, we have proved that a closed equipotential surface with no charge within itself must enclose an equipotential volume.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Long Answer Type Question
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Very short type question
Explore 5 Videos
- ELECTROMAGNETIC WAVESBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:LONG ANSWER
Explore 5 Videos
- MAGNETISM AND MATTER Book:NCERT EXEMPLAR ENGLISHChapter:MAGNETISM AND MATTER Exercise:All Questions
Explore 24 Videos
Similar Questions
Nature of equipotential surface for a point charge is
View Solution(i) Two isolated metal spheres A and B have radii R and 2R respectively and same charge q. Find which of the two spheres have
(a) greater capacitance
(b) greater energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the region of weak field. Draw equipotential surfaces for an electric dipole.
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.
View Solution
Knowledge Check
Assertion: For a point charge concentric spheres centered at a location of the charge are equipotential surfaces.
Reason : An equipotential surface is a surface over which potential has zero value.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
Assertion (A) A spherical equipotential surface is not possible for a point charge.
Reason (R ) A spherical equipotential surface is possible inside a spherical capacitor.
View SolutionWhat is the geometrical shape of equipotential surface due to a single isolated charge ?
View SolutionWhat is the geometrical shape of equipotential surfaces due to a single isolated charge ?
View SolutionFigure shows sone equipotential surfaces produce by some charges. At which point, the value of electric field is greatest ?
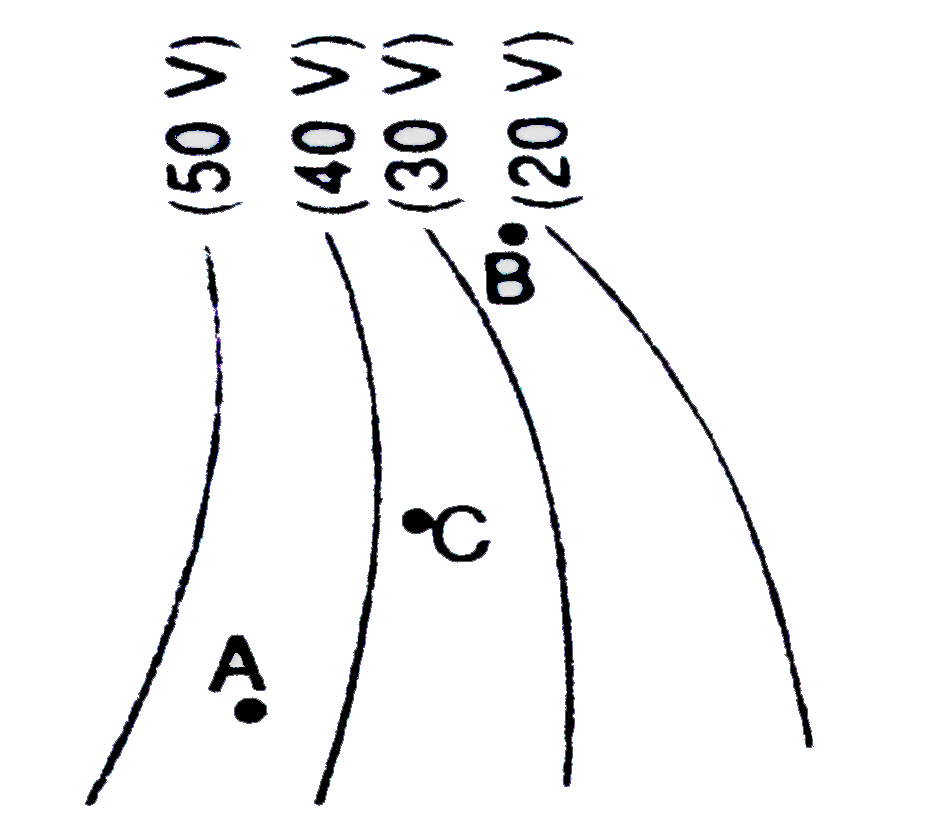
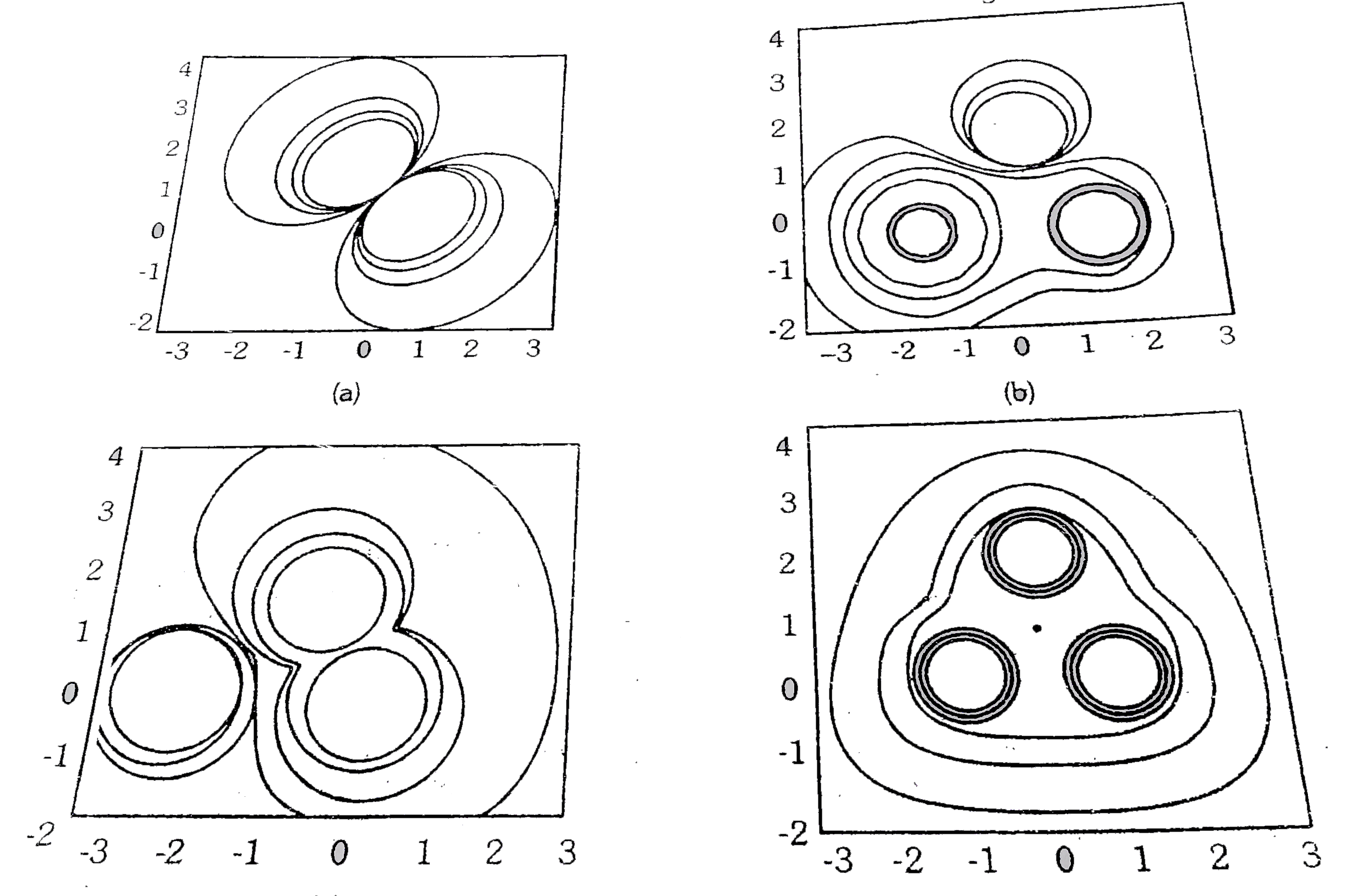
View SolutionThree equal charges are placed at the corners of an equilateral triangle. Which of the graph below correctly depicts the equally-spaced equipotential surfaces in the plane of the triangle? (All graph have the same scale).
View SolutionDefine an equipotential surface. Draw equipotential surfaces :
(i) in the case of single point charge and
(ii) in a constant electric field in Z-direction.
Why the equpotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Given reason.
View SolutionIf a unit positive charge is taken from one point to another over an equipotential surface ,then
View Solution

