Consider two conducting spheres of radii R1andR2 with R1>R2. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whetehr the charge density of the smaller sphere is more or less than that of the larger oe.
To solve the problem, we need to analyze the relationship between the charge density of two conducting spheres that are at the same electric potential. Let's denote the radii of the spheres as R1 and R2, where R1>R2.
1. Understanding the Potential of a Sphere:
The electric potential V of a conducting sphere is given by the formula:
V=kQR
where k is Coulomb's constant, Q is the charge on the sphere, and R is its radius.
2. Setting Up the Equations:
For the two spheres, we have:
V1=kQ1R1(for the larger sphere)
V2=kQ2R2(for the smaller sphere)
Since both spheres are at the same potential, we can set these equations equal to each other:
kQ1R1=kQ2R2
3. Simplifying the Equation:
We can cancel k from both sides:
Q1R1=Q2R2
Rearranging gives us:
Q1=Q2R1R2
4. Understanding Charge Density:
The surface charge density σ is defined as:
σ=QA
where A is the surface area of the sphere. The surface area of a sphere is given by A=4πR2. Therefore, we can express the charge densities for both spheres as:
σ1=Q14πR21(for the larger sphere)
σ2=Q24πR22(for the smaller sphere)
5. Substituting for Charges:
Now substituting Q1 in terms of Q2:
σ1=Q2R1R24πR21=Q24πR2R1
Thus, we have:
σ1=Q24πR2R1
6. Finding the Ratio of Charge Densities:
To compare σ1 and σ2, we can take the ratio:
σ1σ2=Q24πR2R1Q24πR22=R22R1R2=R2R1
Since R1>R2, it follows that:
R2R1<1
Therefore, we conclude:
σ1<σ2
7. Conclusion:
This means that the charge density on the larger sphere (σ1) is less than that on the smaller sphere (σ2).
Final Answer:
The charge density of the smaller sphere is more than that of the larger sphere.
The electric potential V of a conducting sphere is given by the formula:
V=kQR
where k is Coulomb's constant, Q is the charge on the sphere, and R is its radius.
For the two spheres, we have:
V1=kQ1R1(for the larger sphere)
V2=kQ2R2(for the smaller sphere)
Since both spheres are at the same potential, we can set these equations equal to each other:
kQ1R1=kQ2R2
We can cancel k from both sides:
Q1R1=Q2R2
Rearranging gives us:
Q1=Q2R1R2
The surface charge density σ is defined as:
σ=QA
where A is the surface area of the sphere. The surface area of a sphere is given by A=4πR2. Therefore, we can express the charge densities for both spheres as:
σ1=Q14πR21(for the larger sphere)
σ2=Q24πR22(for the smaller sphere)
Now substituting Q1 in terms of Q2:
σ1=Q2R1R24πR21=Q24πR2R1
Thus, we have:
σ1=Q24πR2R1
To compare σ1 and σ2, we can take the ratio:
σ1σ2=Q24πR2R1Q24πR22=R22R1R2=R2R1
Since R1>R2, it follows that:
R2R1<1
Therefore, we conclude:
σ1<σ2
This means that the charge density on the larger sphere (σ1) is less than that on the smaller sphere (σ2).
The charge density of the smaller sphere is more than that of the larger sphere.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Short Answer Type Question
Explore 5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Long Answer Type Question
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:MCQ s (More than one Options)
Explore 7 Videos
- ELECTROMAGNETIC WAVESBook:NCERT EXEMPLAR ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:LONG ANSWER
Explore 5 Videos
- MAGNETISM AND MATTER Book:NCERT EXEMPLAR ENGLISHChapter:MAGNETISM AND MATTER Exercise:All Questions
Explore 24 Videos
Similar Questions
Three plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is

View SolutionA conducting sphere of radius r has a charge . Then .
View Solution
Knowledge Check
Consider two conductinbg spheres of radill R1andR2 with R1>R2. If the two are at the same potential, and the larger sphere has more charge than the smaller sphere, then
Athe charge density of smaller sphere is less then that of larger sphere,Bthe charge density of smaller sphere is more than that of larger sphere.Cboth spheres may have same charge density.Dnone of these
Two charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View SolutionA charge Q has been divided on two concentirc conducting spheres of radii R1andR2(R1>R2) such that the surface charge densities on both the sphere is same. Find the potential at their common center.
View SolutionCharge on the outer sphere is q, and the inner sphere is grounded. Then the charge q' on the inner sphere is q', for
(r2>r1)

View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionConsider two solid sphere of radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitational field due to sphere 1 and 2 are shown. The value of M1M2) is:
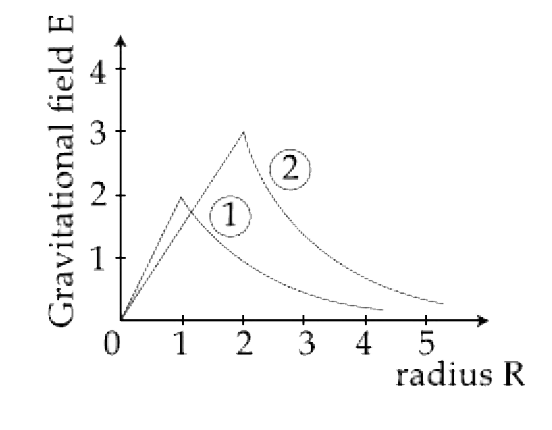
View Solution

