A circuilar disc of radius 'R' is placed co-axially and horizontally inside and opaque hemispherical bowl of radius 'a', Fig. The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index μ and the near edge of the dise becomes just visible. How far below the top of the bowl is the disc placed ?
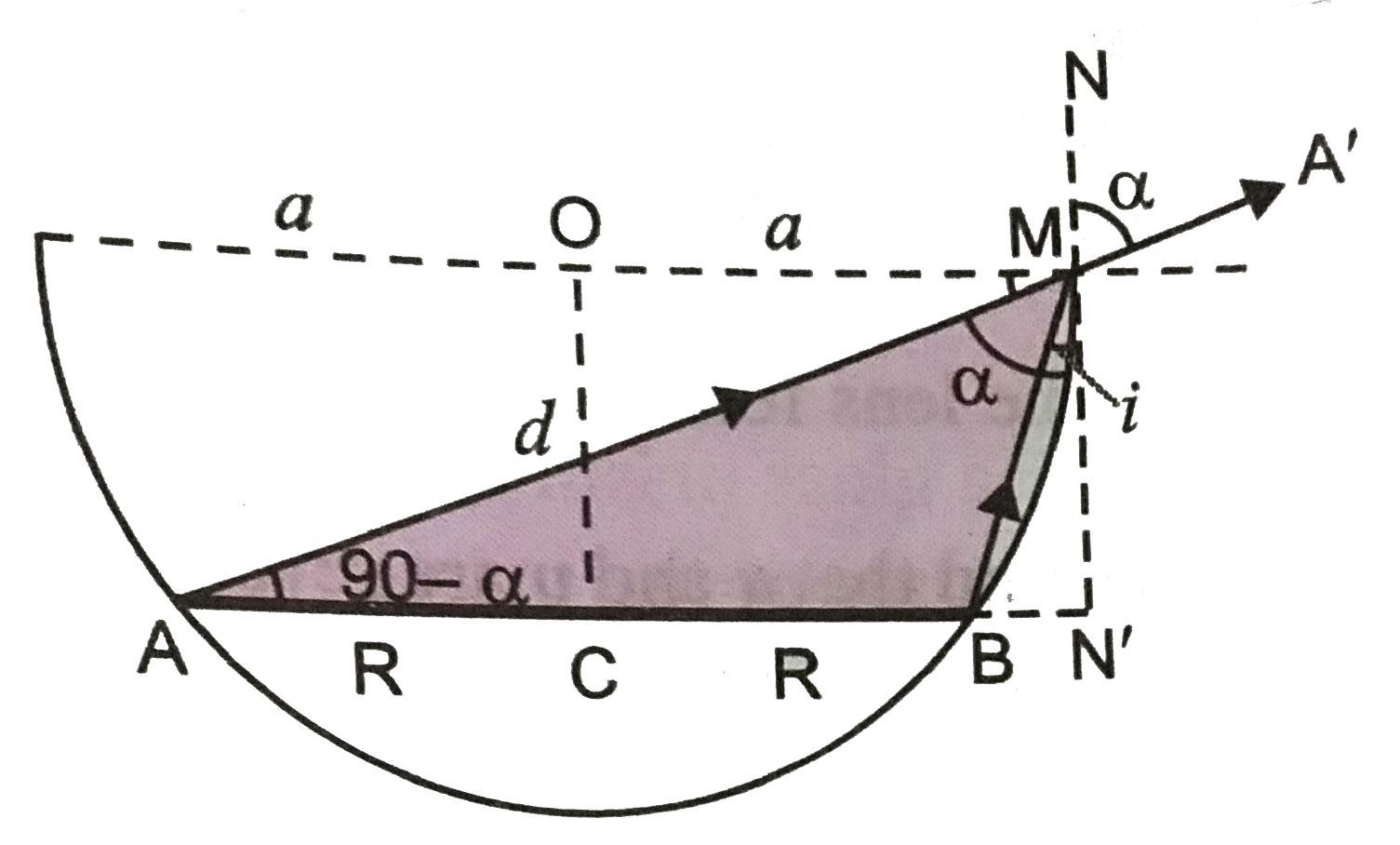 .
.
Refering to the figure, AM is the direction of incidence ray before liquid is filled. After liquied is filled in, BM is the direction of the incident ray. Refracted ray in both cases is same as the along. AM.
Let the disc is separated by O at a distance d as shown in figure. Also, considering angle
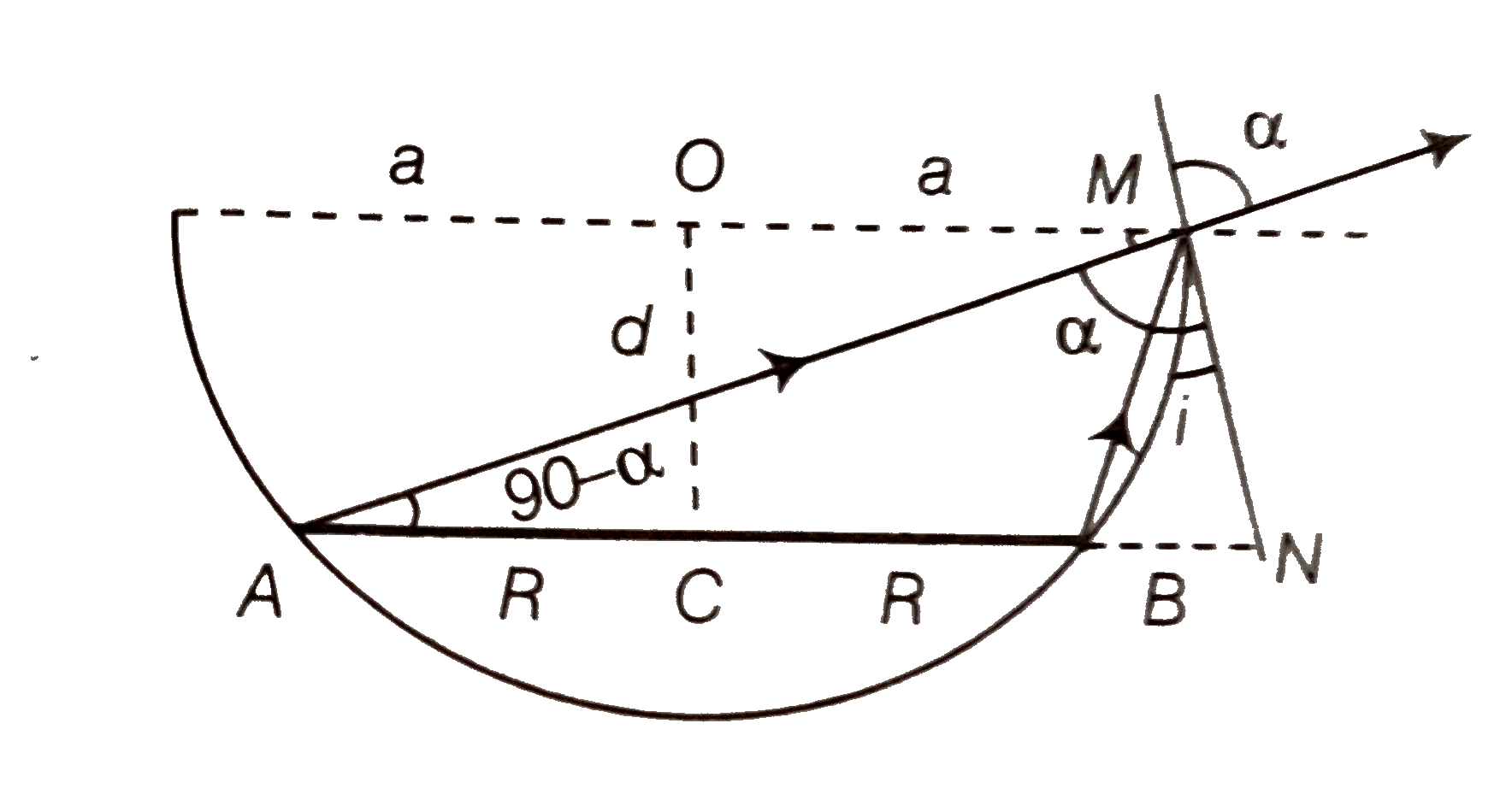
=90∘,OM=a,CB=NB=a−R,AN=a+R
Hence , in figure
sint=a−R√d2+(a−R)2
and sinα=cos(90−α)=a+R√d2+(a+R)2
But on applying Snell's law.
1μ=sintsinr=sintsinα
On substtituting the values, we have the sepration
d=μ(a2−b2)√(a+r)2−μ(a−r)2
This is required expression
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTS Book:NCERT EXEMPLAR ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTS Exercise:MULTIPLE CHOICE QUESTIONS (MORE THAN ONE OPTIONS )
Explore 6 Videos
- NUCLEIBook:NCERT EXEMPLAR ENGLISHChapter:NUCLEIExercise:Long answer type question
Explore 10 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITBook:NCERT EXEMPLAR ENGLISHChapter:SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITExercise:Multiplel choice questions
Explore 26 Videos
Similar Questions
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
View Solution
A small mass of 10 g lies in a hemispherical bowl of radius 0.5 m at a height of 0.1 m from the bottom of the bowl. The mass will be in equilibrius if the bowl rotates at an
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA small ball is pushed from a height h along a smooth hemispherical bowl of radius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
View SolutionA hemispherical bowl is made of steel 0.5 cm thick. The inside radius of the bowl is 4cm.
View SolutionA hemispherical bowl is made of steel 0.5 cm thick. The inside radius of the bowl is 4cm. find volume of steel
View SolutionA small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.
View Solution