If each diode in figure has a forward bias resistance of 25 Omega and infinite resistance in reverse bias, what will be the values of the current I1,I2,I3andI4?
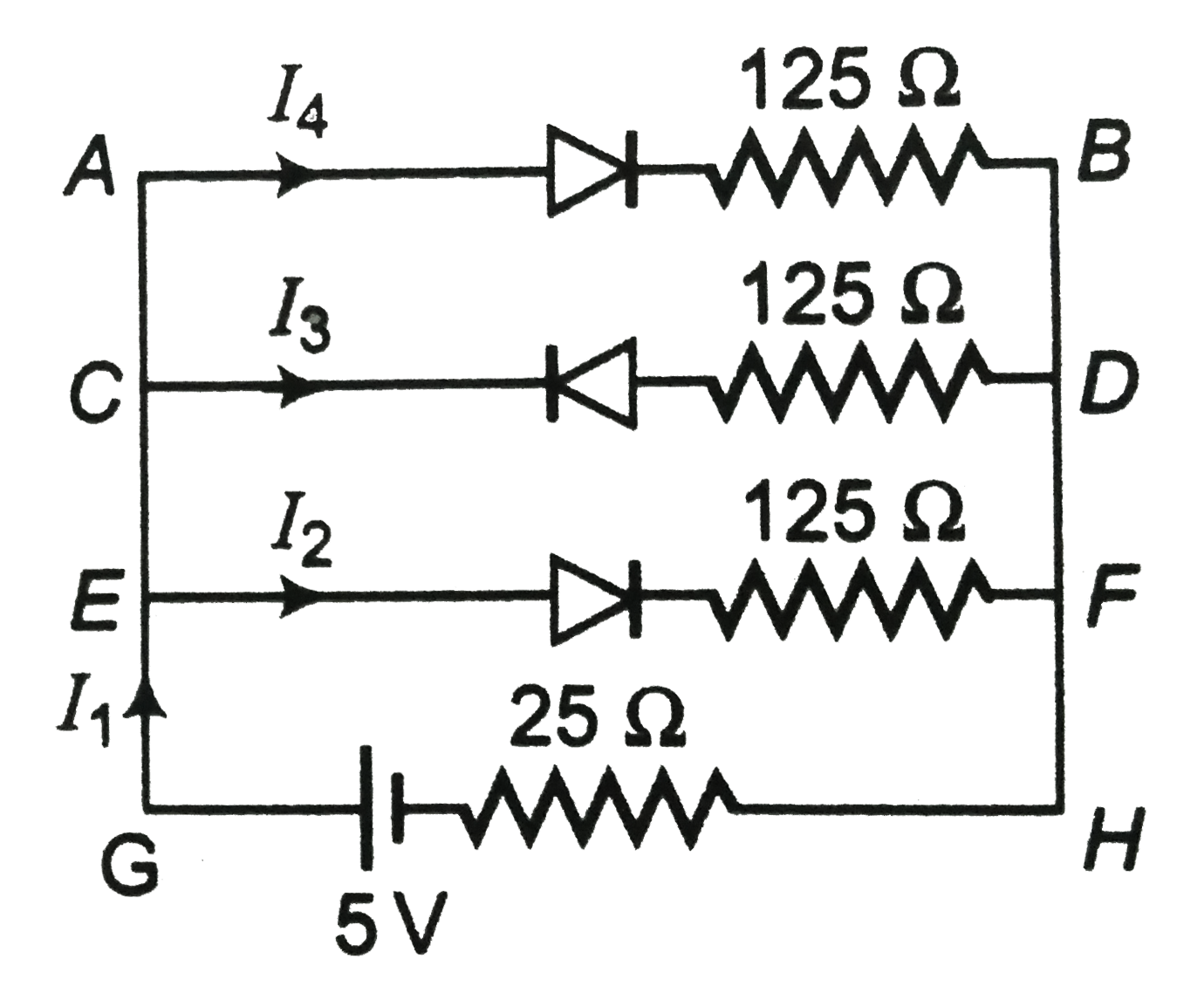
Given, forward biased reistance =25Ω
Reverse biased resistance =∞
As the diode in branch CD is in reverse biased which having resistance infinite,
so I3=0
Resistance in branch AB=25+125=150Ω say R1
Resistance in branch EF=25+125=150Ω say R2
AB is parallel to EF.
So, resutant resistance 1R'=1R1+1R2=1150+1150=2150
⇒R'=75Ω
Total resistance R=R'+25=75+25=100Ω
Current I1=VR=5100=0.05A
I1=I4+I2+I3
So, I1=I4+I2
Here, the resistances R1 and R2 is same.
i.e., I4=I2
∴I1=2I2
⇒I2=I12=0.052=0.025A
and I4=0.025A
Thus, I1=0.05A,I2=0.025A,I3=0 and I4=0.025A
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - NUCLEIEXERCISE - Very short Anwer type question14videos
NUCLEI
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions7videos
MOVING CHARNGES AND MAGNETISM
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS16videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
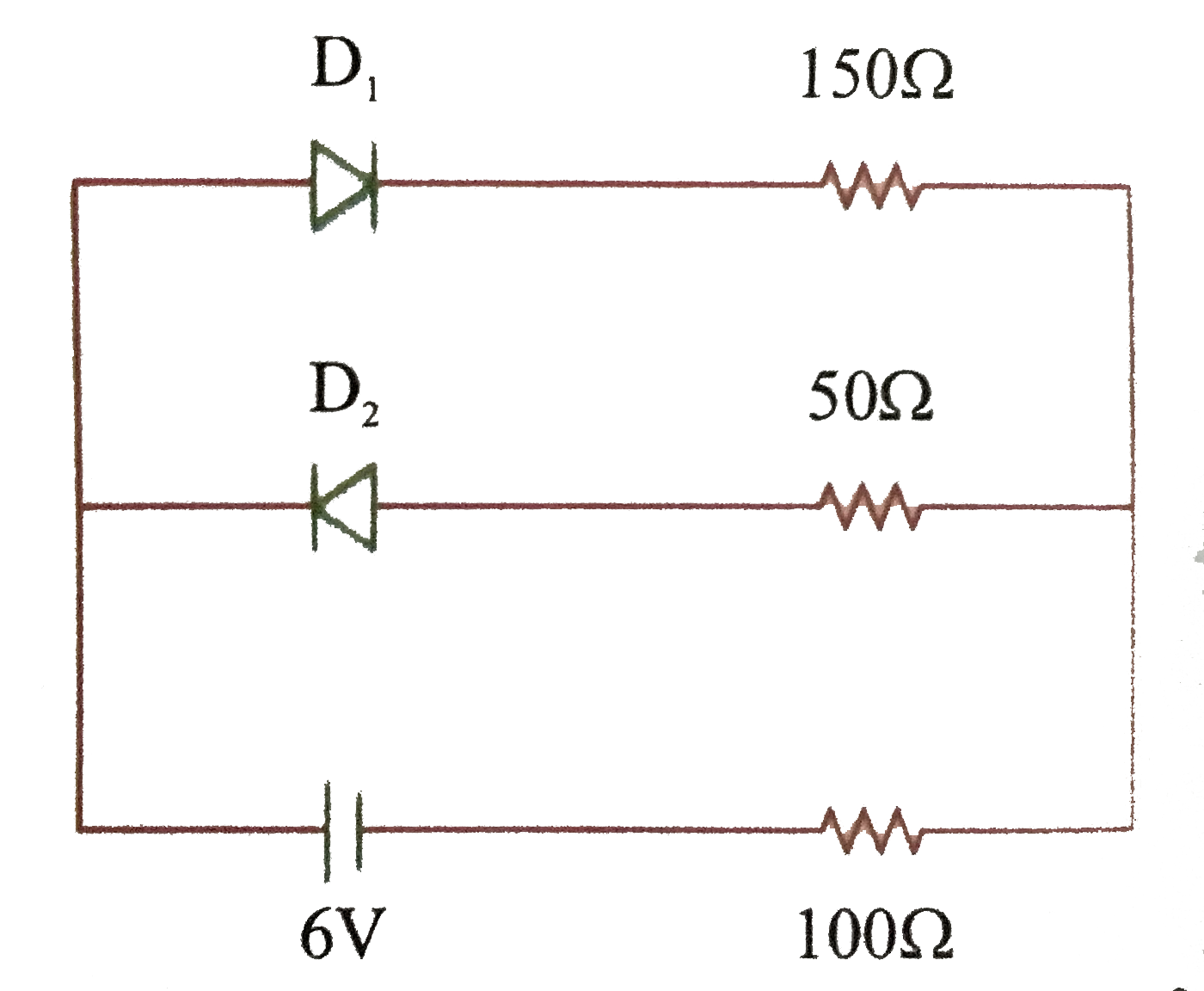
The circuit shown in figure (1) Contains two diodes each with a forward resistance of 50ohm and with infinite reverse resistance. If the battery voltage is 6V, the current through the 100ohm resistance is.
 .View Solution
.View SolutionThe circuit shown in the figure contains two diodes each with a forward resistance of 50Ω and with infinite backward resistance. If the batter of 6 V is connected in the circuit, then the current through the 100Ω resistance is
View Solution
Knowledge Check
- Question 1 - Select One
In the circuit shown, the value of currents I1,I2andI3 are
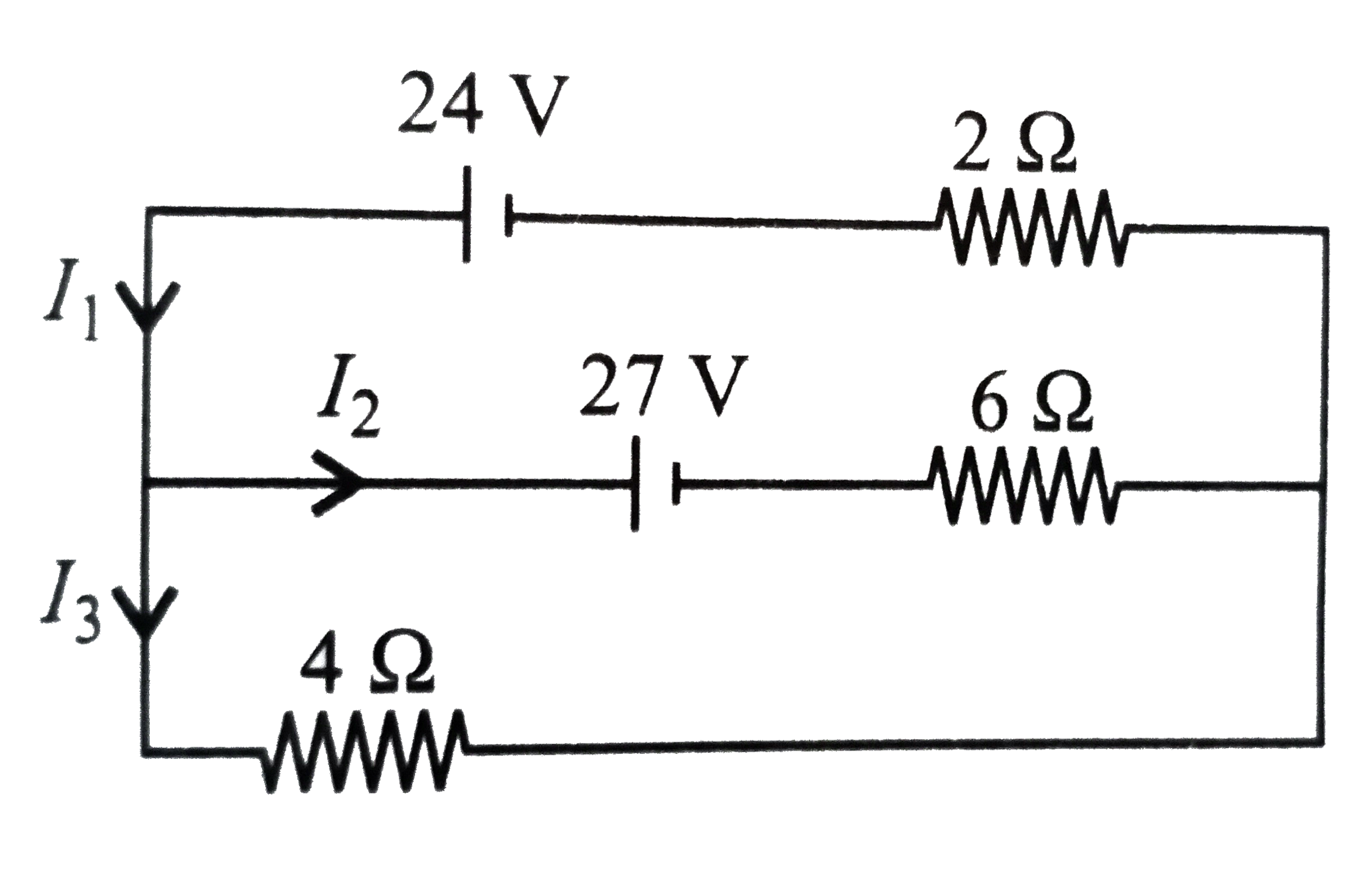 A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A - Question 2 - Select One
The circuit shown in the figure contains two diodes each with a forward resistance of 30 Ω and with infinite backward resistance. If the battery is 3 V, the current through the 50 Ω resistance (in ampere) is
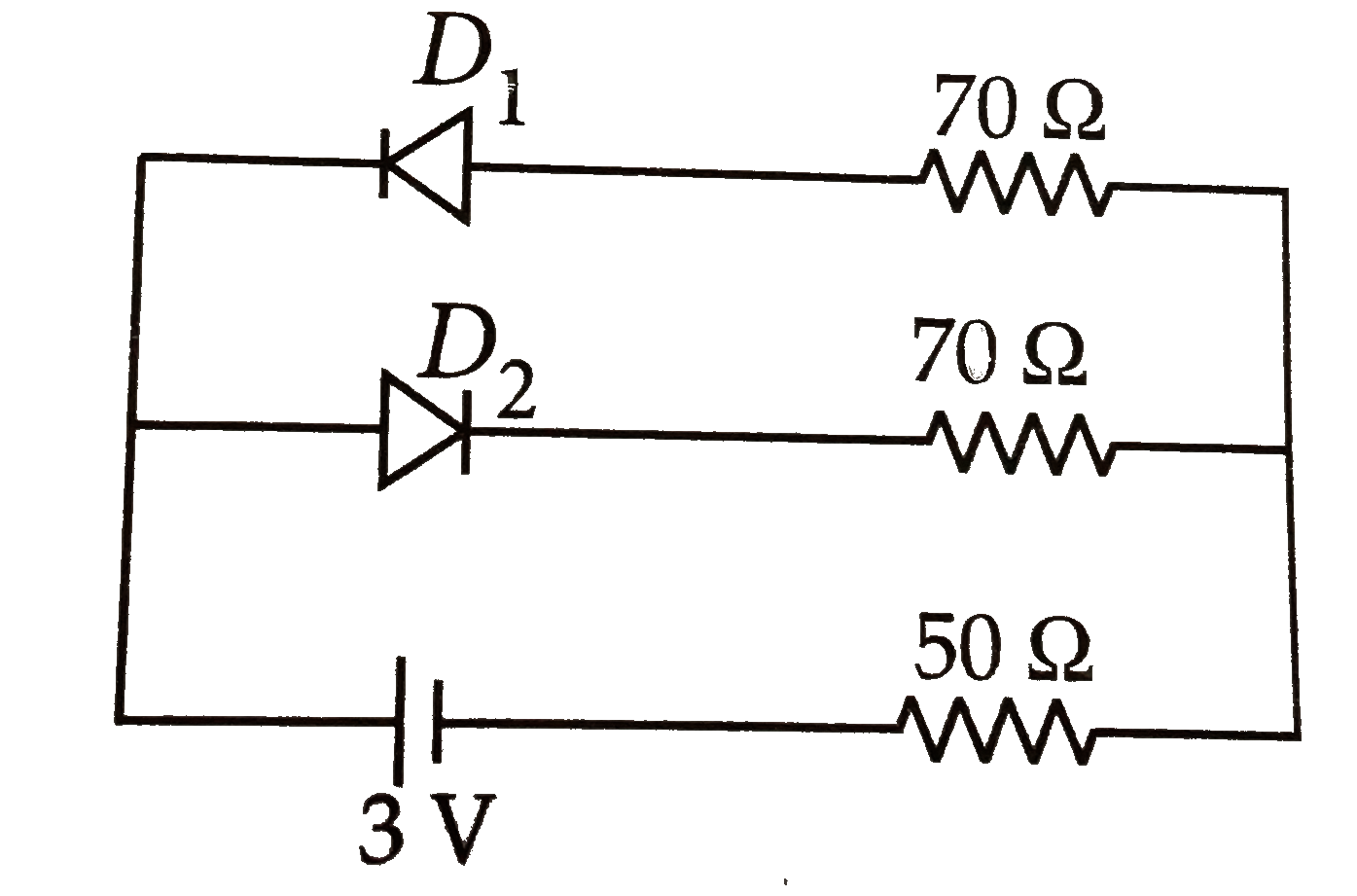 AzeroB0.01C0.02D0.03
AzeroB0.01C0.02D0.03
In the circuit shown in the figure
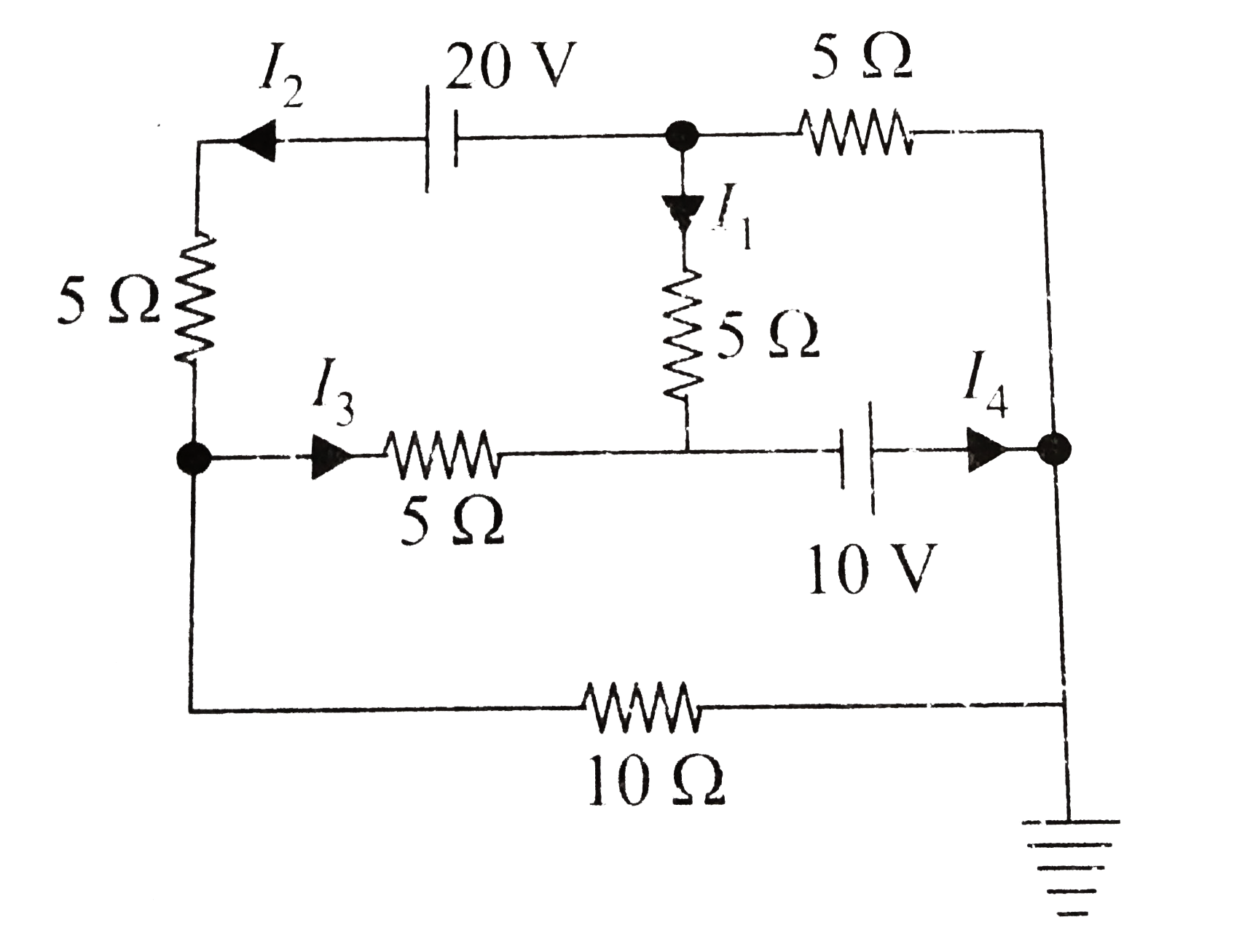 .
.
The value of current I4 isView SolutionThe circuit shown in figure contains two diodes each with a forward resistance of 50Ω and infinite reverse resistance.If the battery voltage is 6 v ,then the current through the 100Ω resistance is
View SolutionEach resistor shown in figure is an infinite network of resistance1Ω. The effective resistance Between points A and B is
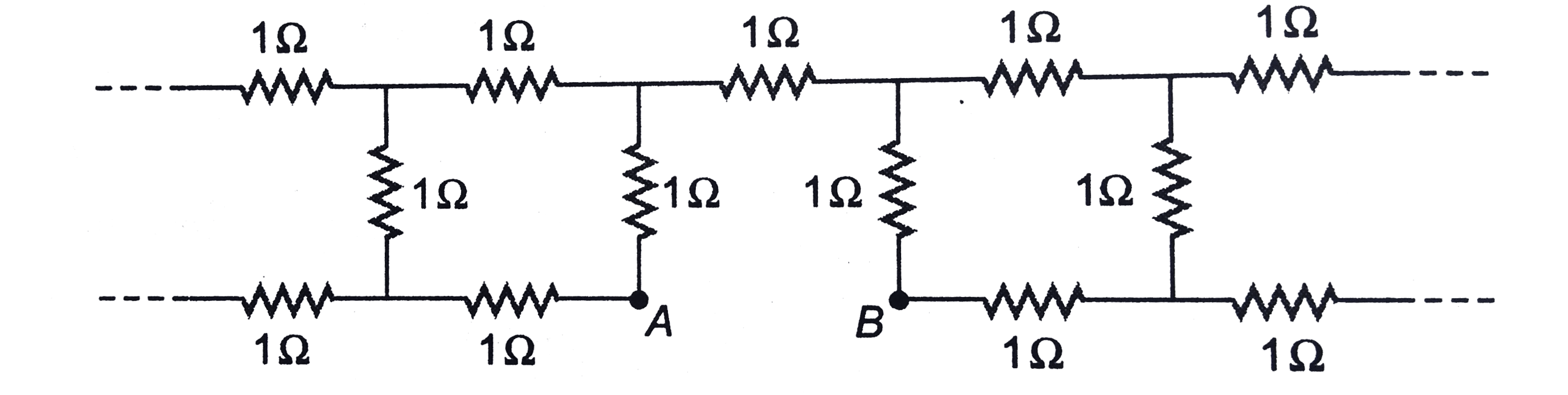 View Solution
View SolutionCalculate the values of currents I1,I2,I3,andI4 in the section of networks shown in Fig 5.64
 View Solution
View SolutionA 2V battery may be connected across the points A and B as shown in figure. Assume that the resistance of each diode is zero in forward bias and infinity in reverse bias.Find the current supplied by the battery if the positive terminal of the battery is connected to (a) the point A (b)the point B.
 View Solution
View SolutionIn the circuit as shown in figure, the ratio of current i1/i2 is
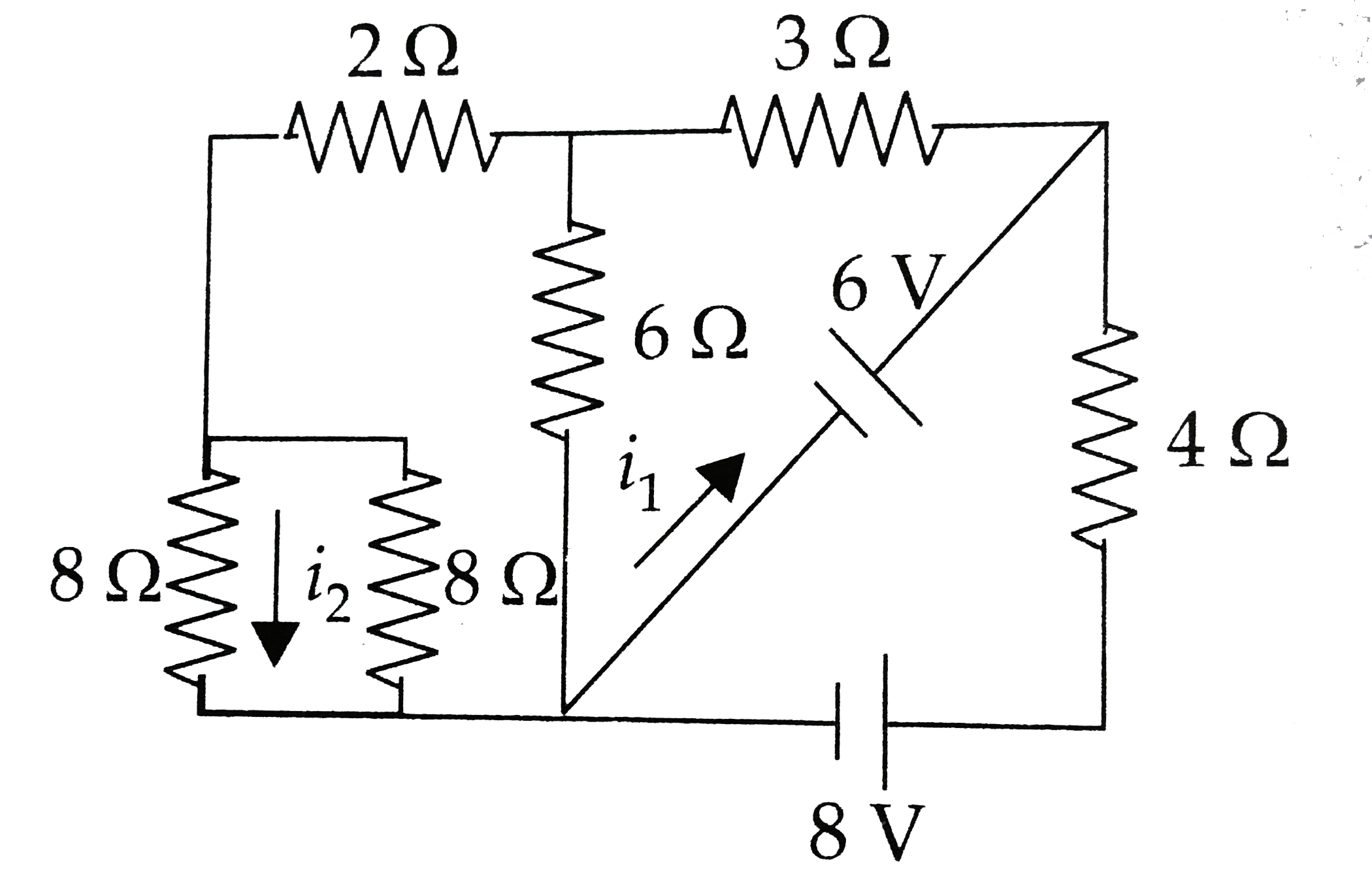 View Solution
View Solution
