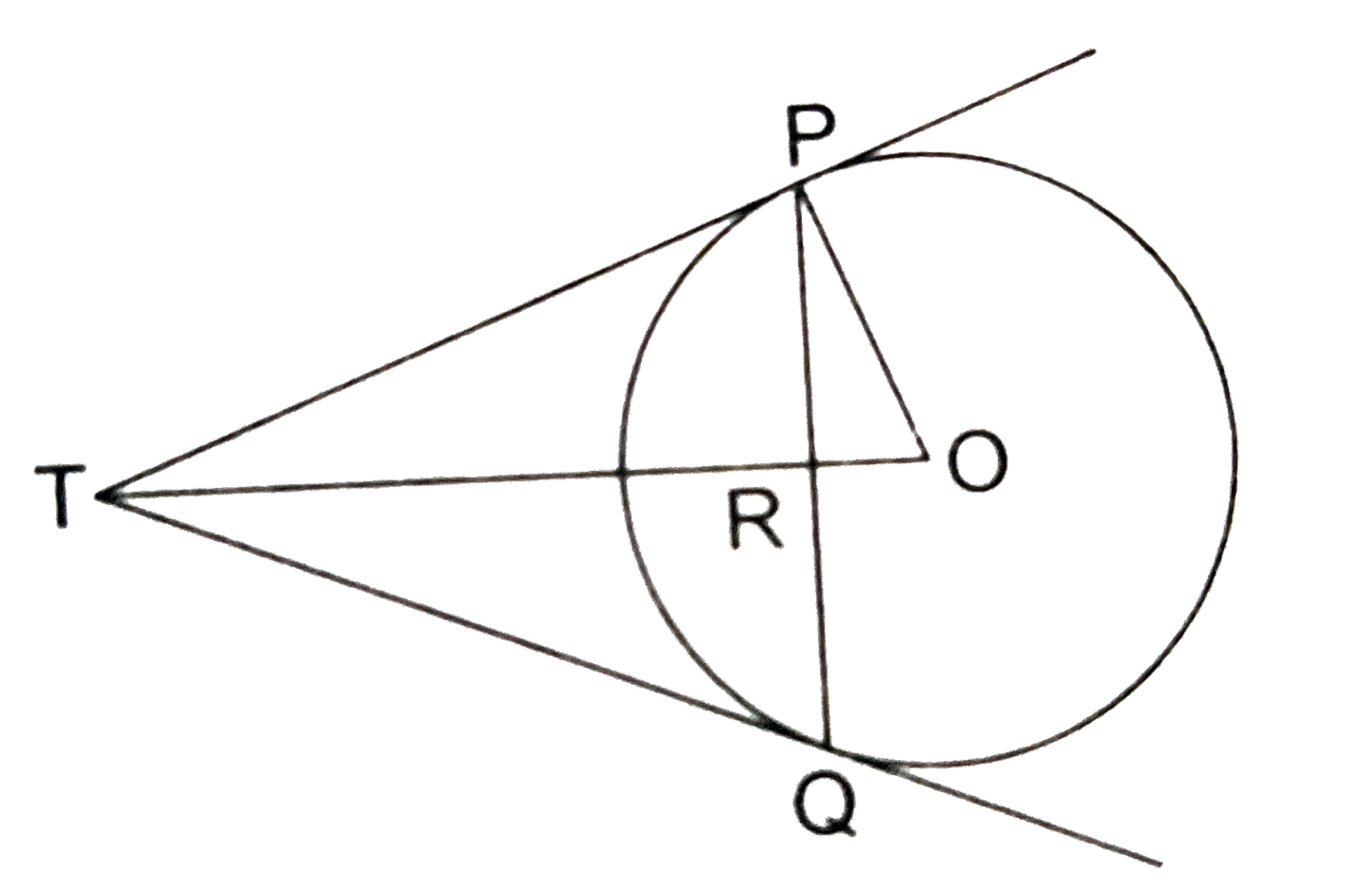
PQ is a chord of length 4.8cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
Video Solution
Text Solution
R is the midpoint of PQ, i.e., PR=QR=(12×4.8)cm=2.4cm.
Also, TO⊥PQ.
In right ΔPRO, we have
PO2=PR2+RO2⇒RO=√PO2−PR2
=√32−2.42=√3.24=1.8.
Let TR=x and TP=y.
In right ΔPTR, we have TP2=TR2+PR2⇒y2=x2+(2.4)2.........(i)
In right ΔOTP, we have
TO2=TP2+PO2⇒(TR+RO)2=TP2+PO2
⇒(x+1.8)2=y2+32⇒x2+3.6x+3.24=y2+9. ............(ii)
Solving (i) and (ii) , we get x=3.2, y=4.
∴TP=4cm.
|
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself
20 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cmPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cmPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A163 cmB203 cmC185 cmD196 cm
AB is a chord of length 24cm of a circle of radius 13cm .The tangents at A and B intersect at a point C. Find the length AC
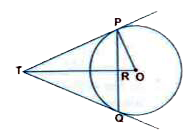
View SolutionIn Fig , PQ is a chord of length 16 cm, of a radius 10 cm . The tangents at P and Q intersect at a point T. Find the length of TP.
View SolutionIn Fig. 10.59, AB is a chord of length 16cm of a circle of radius 10cm. The tangents at A and B intersect at a point P . Find the length of PA . (FIGURE)
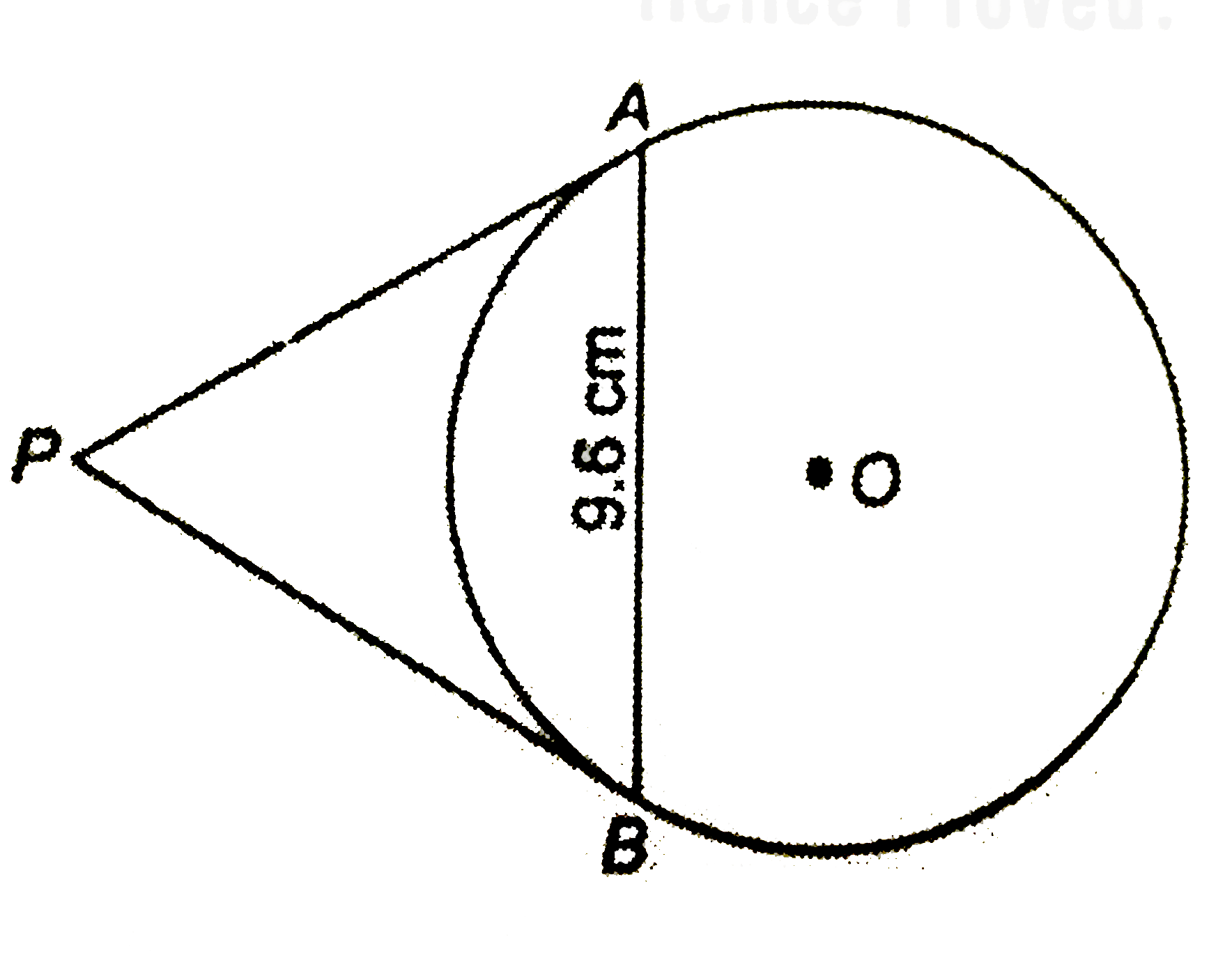
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
View SolutionPQ is chord of length 6 cm of a circle of radius 5 cm. Tangents to the circle at P and Q meet at T. Length of TP is
View Solution
