In the given figure, an isosceles triangle ABC, with AB=AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
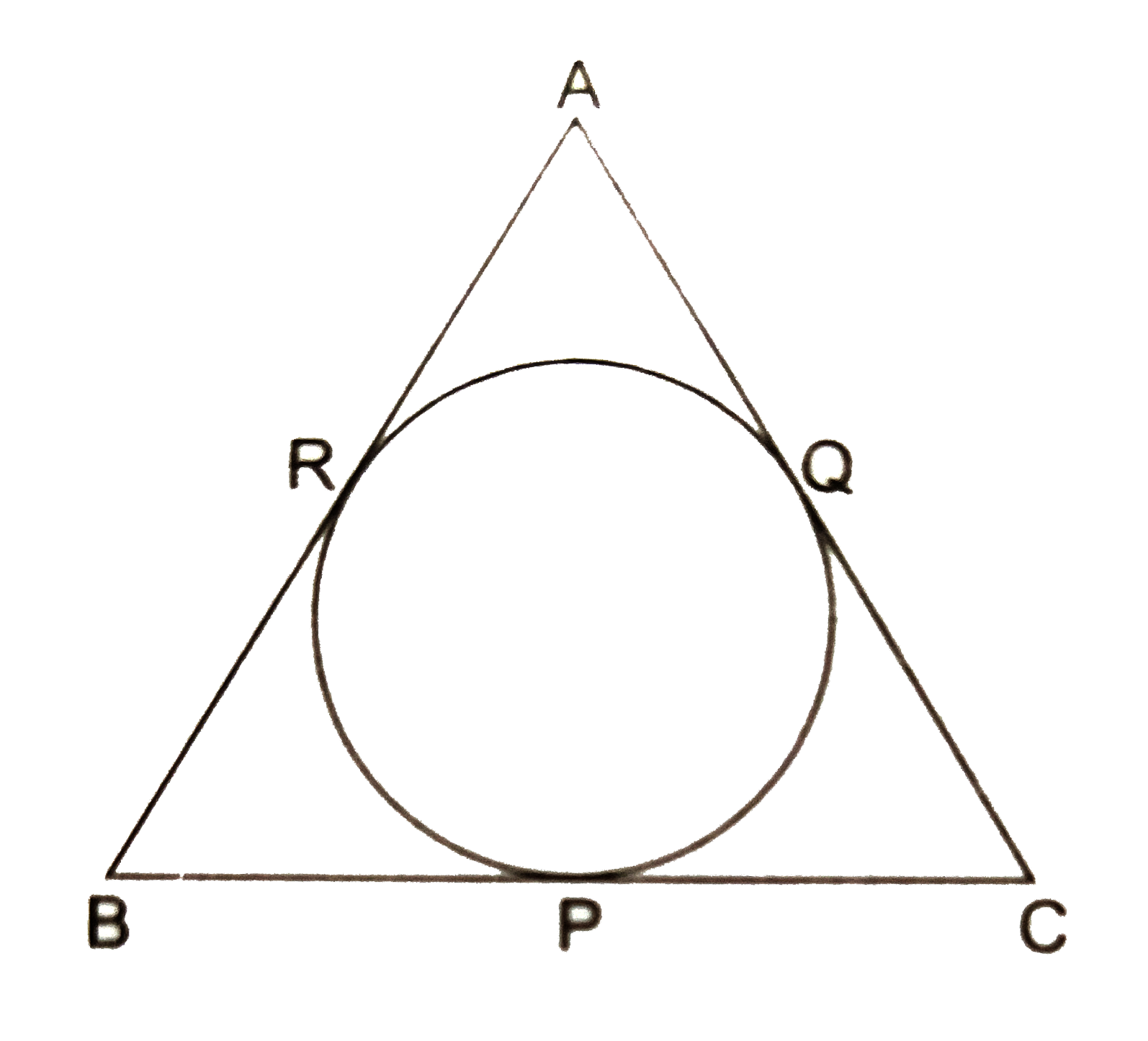
We know that the tangents to a circle from an external point are equal.
∴AQ=AR, BP=BR, CP=CQ.
Now, AB=AC⇒AR+BR=AQ+CQ
⇒AR+BP=AR+CΠmpliesBP=CP
⇒P bisects the base BC.
Topper's Solved these Questions
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Exercise 8B
Explore 15 Videos
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Multiple Choice Questions (Mcq)
Explore 15 Videos
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Test Yourself
Explore 20 Videos
- ARITHMETIC PROGRESSIONBook:RS AGGARWALChapter:ARITHMETIC PROGRESSIONExercise:Multiple Choice Questions (Mcq)
Explore 30 Videos
- CONSTRUCTIONSBook:RS AGGARWALChapter:CONSTRUCTIONSExercise:Test Yourself
Explore 10 Videos
Similar Questions
An isosceles triangle ABC, with AB = AC, circumscribes a circle, touching BC at P, AC at Q and AB at R. Prove that the contact point P bisects BC.
View Solution△ABC is an isosceles triangle in which AB=AC, circumscribed about a circle. Prove that the base is bisccted by the point of contact.
View Solution
Knowledge Check
ABC is an isosceles triangle (AB = AC) circumscribed about a circle. Then, which of the following statements is correct ?
 ABD = ADBAD = CFCBF = CFDAE = BF
ABD = ADBAD = CFCBF = CFDAE = BFABC is isosceles triangle where AB = AC which is circumscribed about a circel. If P is the point where the circle touches the side BC, then which of the following is true?
ABP=PCBBP>PCCBP<PCDBP=12PC
In the given figure, ΔABC is an isosceles triangle in which AB=AC and AE bisects ∠CAD. Prove that AE∣∣BC.
View SolutionIn the given figure, triangle ABC is circumscribing a circle. Find the length of BC, if AF=3 cm, FB=4 cm and AC= 9 cm
View SolutionIn the given figure, ΔABC is circumscribing a circle, then find the length of BC.

View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

View SolutionIn Figure, ABC is an isosceles triangle with AB=AC, BD and CE are two medians of the triangle. Prove that BD=CE
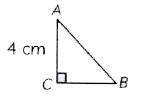
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
View Solution
