In the given figure, ΔABC is an isosceles triangle in which AB=AC and AE bisects ∠CAD. Prove that AE∣∣BC.
To prove that AE∥BC in triangle ΔABC where AB=AC and AE bisects ∠CAD, we can follow these steps:
1. Identify the Given Information:
- ΔABC is an isosceles triangle with AB=AC.
- AE bisects ∠CAD.
2. Assign Angles:
- Let ∠CAB=∠ACB=x (since AB=AC).
- Therefore, ∠ABC=180∘−2x (using the triangle angle sum property).
3. Use the Angle Bisector:
- Since AE bisects ∠CAD, we have:
∠DAE=∠EAC=12∠CAD=12(180∘−2x)=90∘−x
4. Find the Angles at Point E:
- Now we know:
∠DAE=90∘−x
∠EAC=90∘−x
5. Identify the Alternate Interior Angles:
- Since AE is a transversal line to the lines BC and AE, we can analyze the angles formed:
- ∠DAE and ∠ABC are alternate interior angles.
- We have already established that:
∠DAE=90∘−x
∠ABC=180∘−2x
- To show that AE∥BC, we need to show that ∠DAE=∠ABC.
6. Set Up the Equation:
- From the previous steps, we know:
∠DAE=90∘−x
∠ABC=180∘−2x
- Setting them equal:
90∘−x=180∘−2x
7. Solve for x:
- Rearranging gives:
2x−x=180∘−90∘
x=90∘
- This shows that the angles are equal.
8. Conclusion:
- Since ∠DAE=∠ABC, by the Alternate Interior Angles Theorem, we conclude that:
AE∥BC
- ΔABC is an isosceles triangle with AB=AC.
- AE bisects ∠CAD.
- Let ∠CAB=∠ACB=x (since AB=AC).
- Therefore, ∠ABC=180∘−2x (using the triangle angle sum property).
- Since AE bisects ∠CAD, we have:
∠DAE=∠EAC=12∠CAD=12(180∘−2x)=90∘−x
- Now we know:
∠DAE=90∘−x
∠EAC=90∘−x
- Since AE is a transversal line to the lines BC and AE, we can analyze the angles formed:
- ∠DAE and ∠ABC are alternate interior angles.
- We have already established that:
∠DAE=90∘−x
∠ABC=180∘−2x
- To show that AE∥BC, we need to show that ∠DAE=∠ABC.
- From the previous steps, we know:
∠DAE=90∘−x
∠ABC=180∘−2x
- Setting them equal:
90∘−x=180∘−2x
- Rearranging gives:
2x−x=180∘−90∘
x=90∘
- This shows that the angles are equal.
- Since ∠DAE=∠ABC, by the Alternate Interior Angles Theorem, we conclude that:
AE∥BC
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXAMPLE
10 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 8
13 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)
73 Videos
Similar Questions
Knowledge Check
In the given figure, △ABC is an isosceles triangle, in which AB=AC, AD⊥BC, BC = 6cm and AD = 4cm. The length of AB is:
दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD⊥BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ? A4 cmB6 cmC7 cmD5 cm
A4 cmB6 cmC7 cmD5 cm
In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
AD⊥BC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
 Prove that:
Prove that:
ΔADB≅ΔADC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
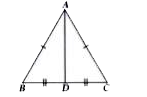 Prove that:
Prove that:
∠BAD=∠CAD
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. If BM⊥ACandCN⊥AB, prove that:
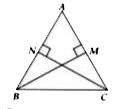
BM = CN
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. If BM⊥ACandCN⊥AB, prove that: ΔBMC≅ΔCNB
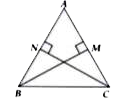
View SolutionIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
View Solution