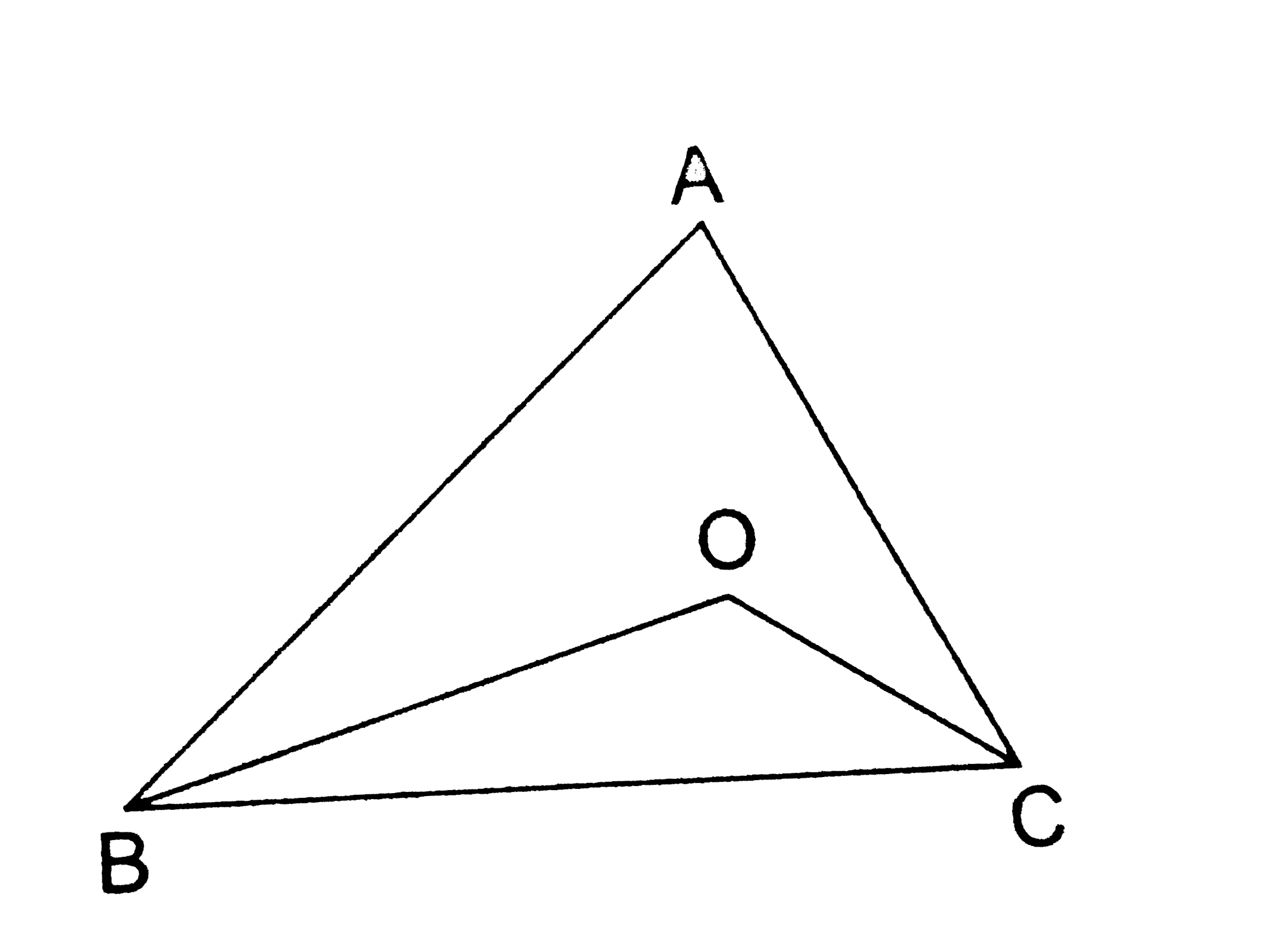
In the given figure, BO and CO are the bisectors of ∠Band∠C respectively. If ∠A=50∘ then ∠BOC=?
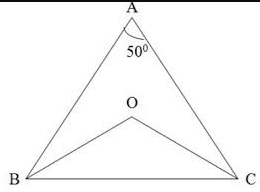
A
130∘
B
100∘
C
115∘
D
120∘
Video Solution
Text Solution
The correct Answer is:C
∠B+∠C=(180∘−∠A)=(180∘−150∘)=130∘
12∠B+12∠C=(12×130∘)=65∘
12∠B+12∠C+∠BOC=180∘⇒65∘+∠BOC=180∘⇒∠BOC=115∘.
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)
2 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)
73 Videos
Similar Questions
Knowledge Check
In a triangle ABC , OB and OC are the bisector of angle ∠B and ∠C respectively . ∠BAC=60∘ . The angle ∠BOC will be :
A150∘B120∘C100∘D90∘The internal bisectors of ∠Band∠C of ΔABC meet at O. If ∠A=80∘ then ∠BOC is :
A50∘B160∘C100∘D130∘In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively, ∠C=70∘and∠D=30∘. Then, ∠AOB=?
A50∘B130∘C80∘D100∘
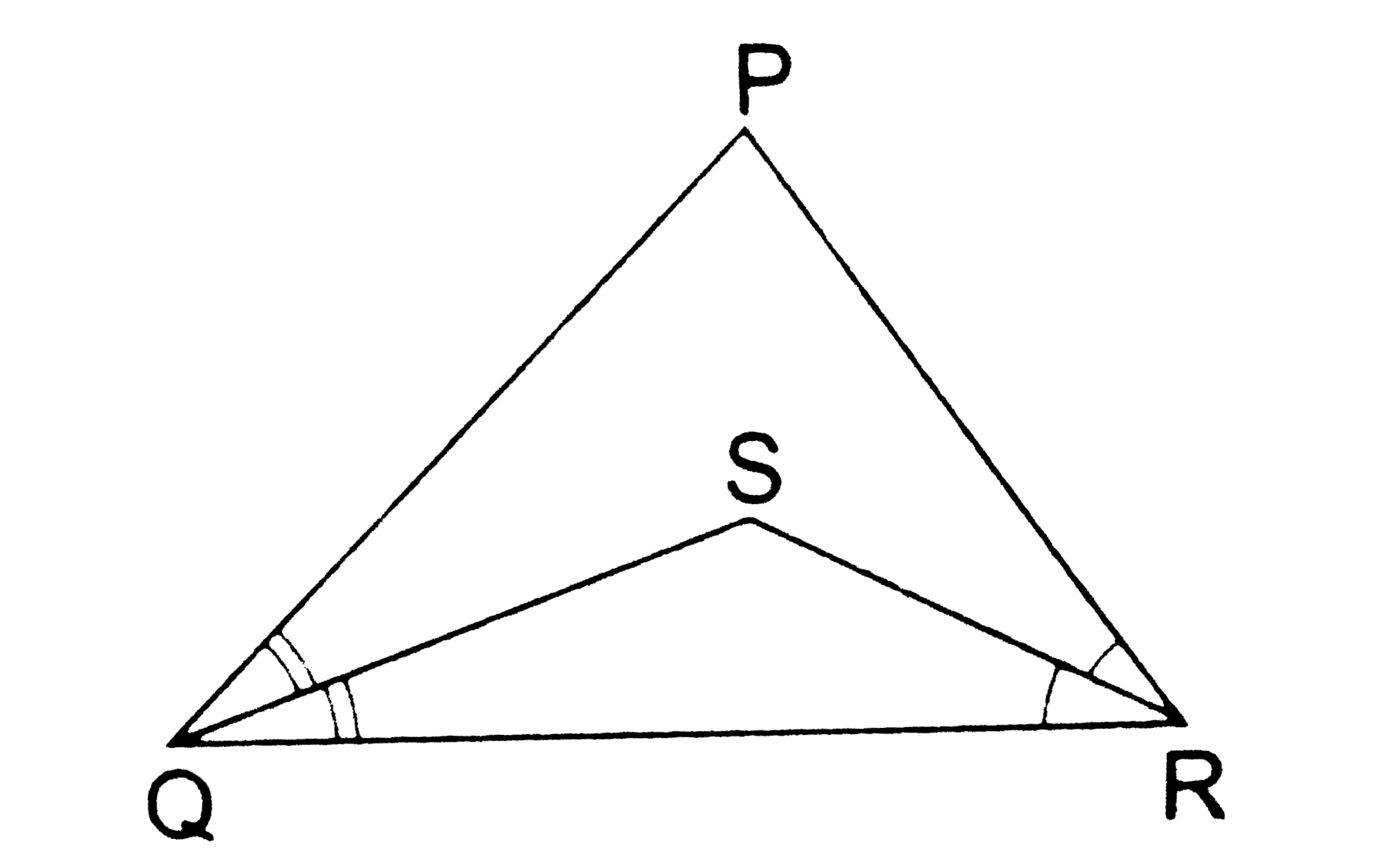
In the given figure, PQ>PR and QS and RS are the bisectors of ∠Qand∠R respectively. Show that SQ>SR.
View SolutionIn the given figure, DE || QR and AP and BP are bisectors of ∠EABand∠RBA, respectively. The value of ∠APB=

View SolutionIn the given figure, AC>AB and AD is the bisector of ∠A. show that ∠ADC>∠ADB.
View SolutionIn the given figure DO and CO are the bisectors of ∠ADC and ∠BCD respectively. If ∠ADC=∠BCD=60∘ and ∠DAB=100∘ find
∠DOC and ∠ABC
View Solution
In the given figure, ray PT is the bisector of ∠QPR.
Find the value of x.

View Solution