In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT=30∘, prove that BA:AT=2:1.
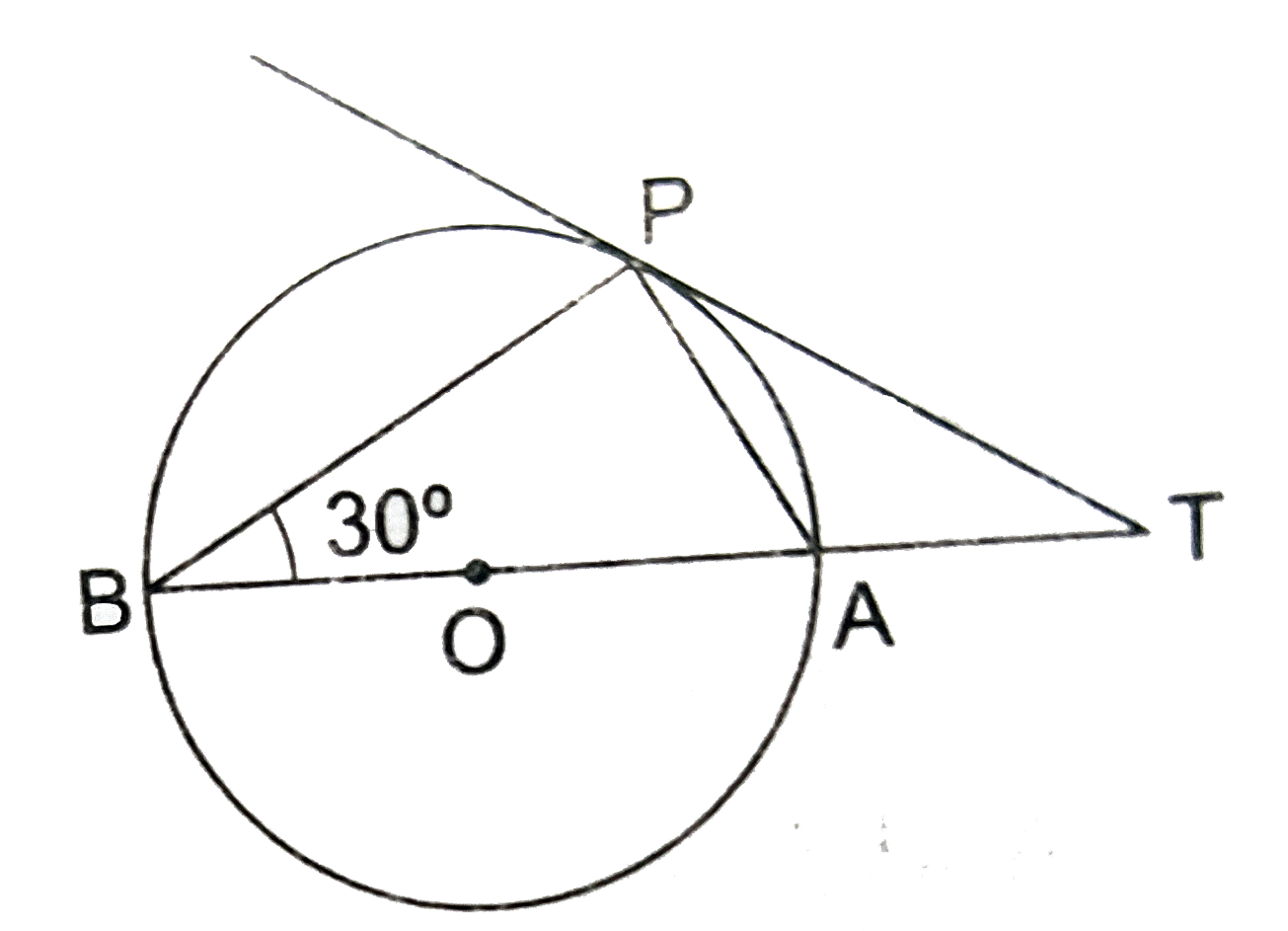
∠APB=90∘ [angle in a semicircle]
∴∠PAB=90∘−∠PBA=90∘−30∘=60∘ [∵∠PBA=∠PBT=30∘]
∠PAT+∠PAB=180∘[ linear pari]
⇒∠PAT=180∘−∠PAB=180∘−60∘=120∘
∠APT=∠PBA=30∘ [angles an alternate segments].
In ΔPAT, we have
∠APT+∠PAT+∠PTA=180∘
⇒∠PTA=180∘−(∠APT+∠PAT)=180∘−(30∘+120∘)=30∘.
Now, ∠APT=∠PTA=30∘⇒AT=AP ..........(i) [sides oppsite equal angles are equal]
In right ΔAPB, we have
cos(∠PAB)=APBA⇒cos60∘=APBA⇒BA=2AP. ..........(ii)
From (i) and (ii), we get BA:AT=2AP:AP=2:1.
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself
20 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
In the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
 A55∘B45∘C75∘D65∘
A55∘B45∘C75∘D65∘In the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
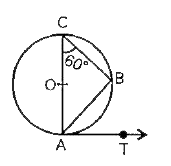 A30∘B60∘C75∘D105∘
A30∘B60∘C75∘D105∘TP and TQ are the tangents to a circle, with centre O. Find x.
 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘
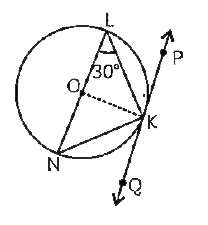
In given figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.

View SolutionIn the figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.
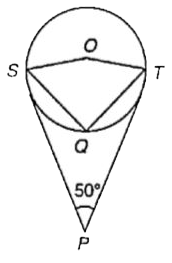
View SolutionIn the given figure 'O' is the centre of the circle SP and TP are the two tangents at S and T respectively. ∠SPT is 50∘, the value of ∠SQT is:
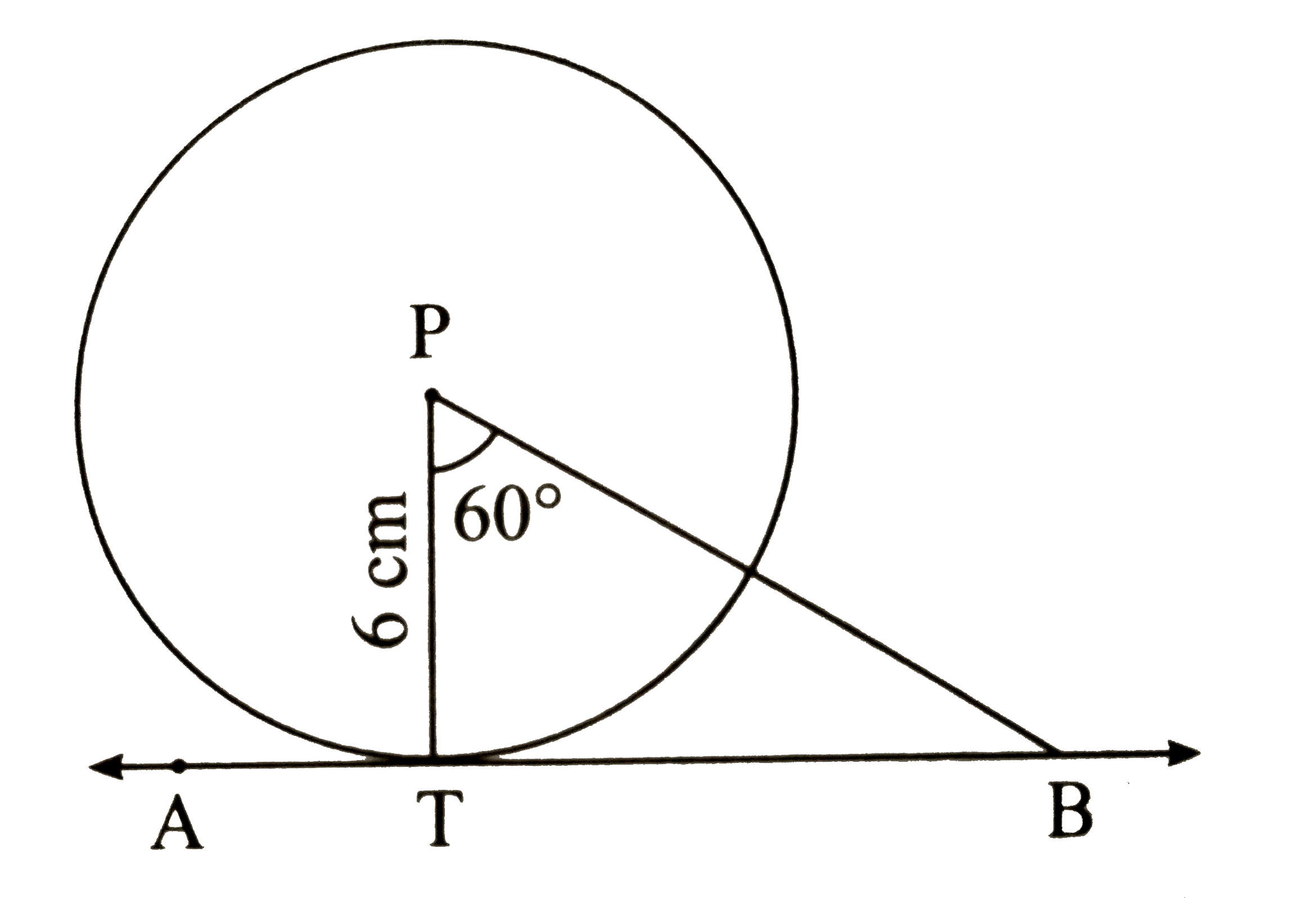
View SolutionIn the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
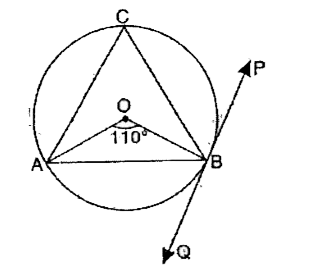
View Solution