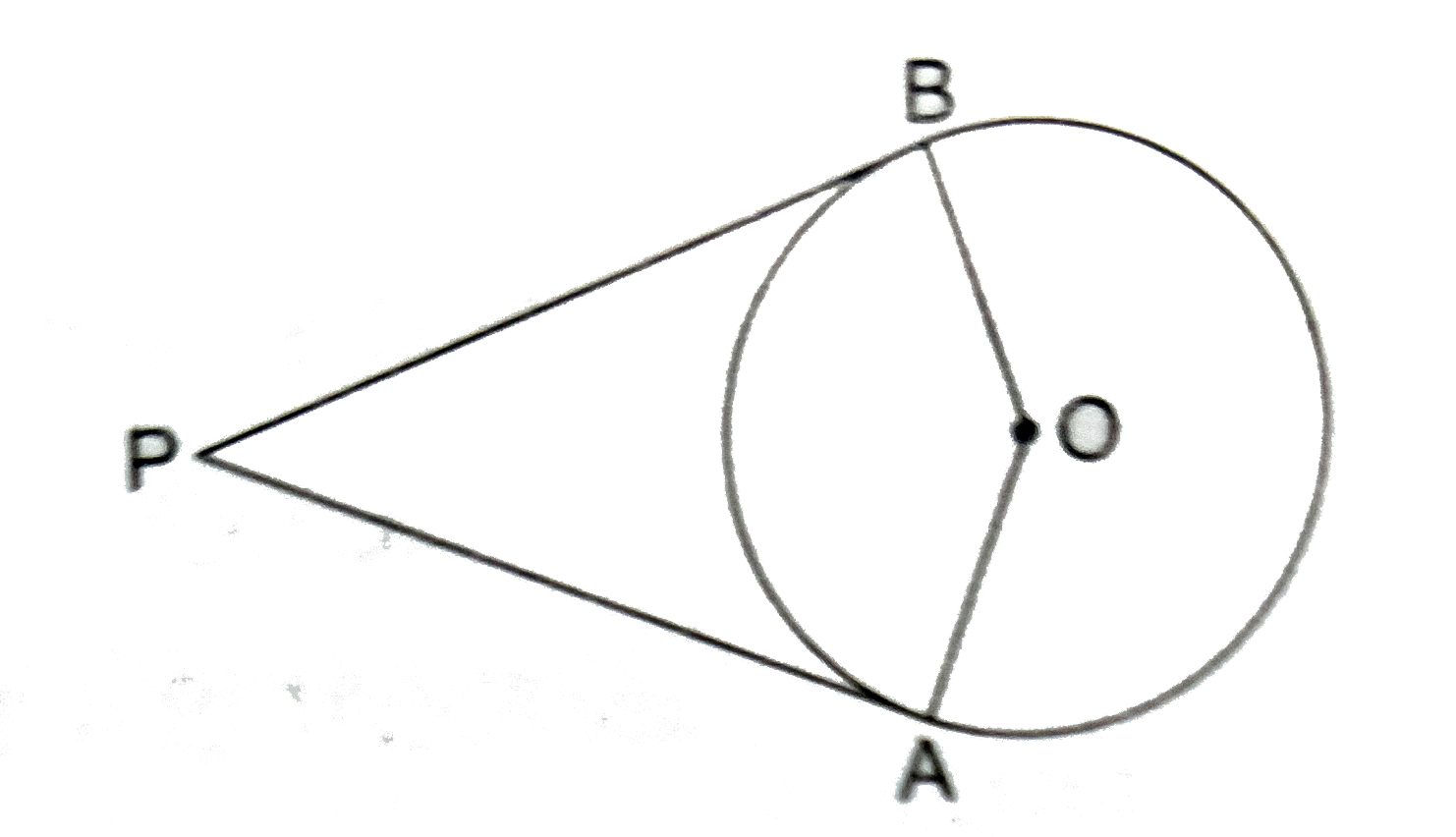
In the given figure, and are the tangent segments to a circle with centre . Show that the points , , and are concyclic.
Video Solution
Text Solution
and
and
quad. is cyclic [ a quad. Is cyclic if the sum of a pair of opposite angles is ].

|
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself
20 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
If PA and PB are two tangents to a circle with centre O such that ∠APB=80∘, then, ∠AOP=?
A40∘B50∘C60∘D70∘In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘In figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
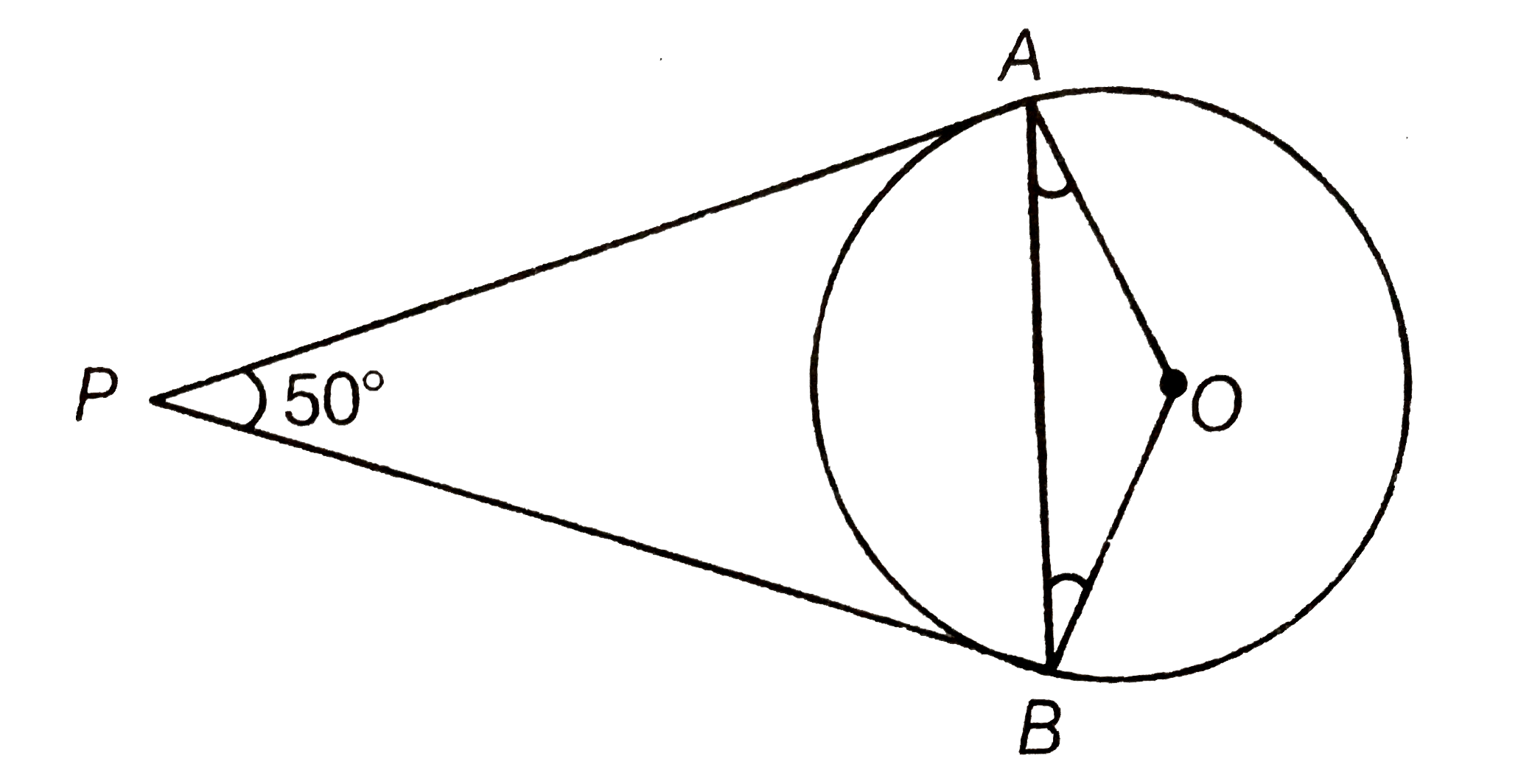 A25∘B30∘C40∘D50∘
A25∘B30∘C40∘D50∘
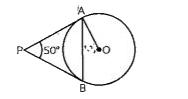
In the figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘, and the measure of ∠OAB is …………
View SolutionIn the given figure PA and PB are tangents to a circle with centre O. if ∠APB=(2x+3)∘ and ∠AOB=(3x+7)∘. then find the value of x.
View SolutionIn the given figure PA and PB are tangents to a circle with centre O.If∠APB=(2x+3)∘ and∠AOB=(3x+7)∘ then, find the value of x.
View SolutionIn the adjoining figure, PA and PB are tangents from P to a circle with center C.If the radius of the circle is 4 cm and PA perpendicular PB.Find the length of the tangent.
View SolutionIn the given figure, AB and AC are tangents to the circle with centre O. Given that ∠BAC=70∘ and P is a point on the minor are BC, find ∠ BPC.
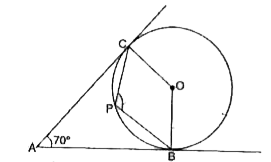
View Solution

