PQ is chord of length 6 cm of a circle of radius 5 cm. Tangents to the circle at P and Q meet at T. Length of TP is
4.75 cm
2.75 cm
3.75 cm
4.25 cm
The correct Answer is:C
To find the length of TP, we will use the properties of circles and right triangles. Here’s a step-by-step solution:
Step 1: Understanding the Geometry
We have a circle with a radius of 5 cm and a chord PQ of length 6 cm. We need to find the length of the tangent TP from point T to point P on the circle.
Step 2: Finding the Midpoint of the Chord
Since PQ is a chord, we can find its midpoint K. The length of the chord PQ is 6 cm, so:
PK=KQ=PQ2=62=3 cm
Step 3: Drawing the Perpendicular from the Center to the Chord
Let O be the center of the circle. We draw a perpendicular line from O to the chord PQ, which meets PQ at K. This perpendicular bisects the chord, so PK = KQ = 3 cm.
Step 4: Applying the Pythagorean Theorem
In the right triangle OPK, we can apply the Pythagorean theorem:
OP2=OK2+PK2
Where:
- OP = radius of the circle = 5 cm
- PK = 3 cm (half the chord length)
- OK = length we need to find
Substituting the values:
52=OK2+32
25=OK2+9
OK2=25−9=16
OK=√16=4 cm
Step 5: Using Similar Triangles
Now, we will use the similarity of triangles. In triangles OPT and PKO:
- Angle OPT = Angle PKO = 90° (both are right angles)
- Angle POT = Angle POK (common angle)
Since the triangles are similar, we can set up the ratio of their corresponding sides:
PTPK=OPOK
Step 6: Substituting Known Values
We know:
- PK = 3 cm
- OP = 5 cm
- OK = 4 cm
Substituting these values into the ratio:
PT3=54
Step 7: Solving for PT
Cross-multiplying gives us:
PT⋅4=3⋅5
4PT=15
PT=154=3.75 cm
Conclusion
The length of TP is 3.75 cm.
---
We have a circle with a radius of 5 cm and a chord PQ of length 6 cm. We need to find the length of the tangent TP from point T to point P on the circle.
Since PQ is a chord, we can find its midpoint K. The length of the chord PQ is 6 cm, so:
PK=KQ=PQ2=62=3 cm
Let O be the center of the circle. We draw a perpendicular line from O to the chord PQ, which meets PQ at K. This perpendicular bisects the chord, so PK = KQ = 3 cm.
In the right triangle OPK, we can apply the Pythagorean theorem:
OP2=OK2+PK2
Where:
- OP = radius of the circle = 5 cm
- PK = 3 cm (half the chord length)
- OK = length we need to find
52=OK2+32
25=OK2+9
OK2=25−9=16
OK=√16=4 cm
Now, we will use the similarity of triangles. In triangles OPT and PKO:
- Angle OPT = Angle PKO = 90° (both are right angles)
- Angle POT = Angle POK (common angle)
PTPK=OPOK
We know:
- PK = 3 cm
- OP = 5 cm
- OK = 4 cm
PT3=54
Cross-multiplying gives us:
PT⋅4=3⋅5
4PT=15
PT=154=3.75 cm
The length of TP is 3.75 cm.
Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.1
Explore 45 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.2
Explore 100 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:EXERCISE(LEVEL 2)
Explore 52 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
Knowledge Check
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A163 cmB203 cmC185 cmD196 cmPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cmPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cm
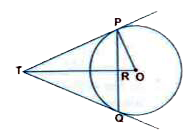
In Fig , PQ is a chord of length 16 cm, of a radius 10 cm . The tangents at P and Q intersect at a point T. Find the length of TP.
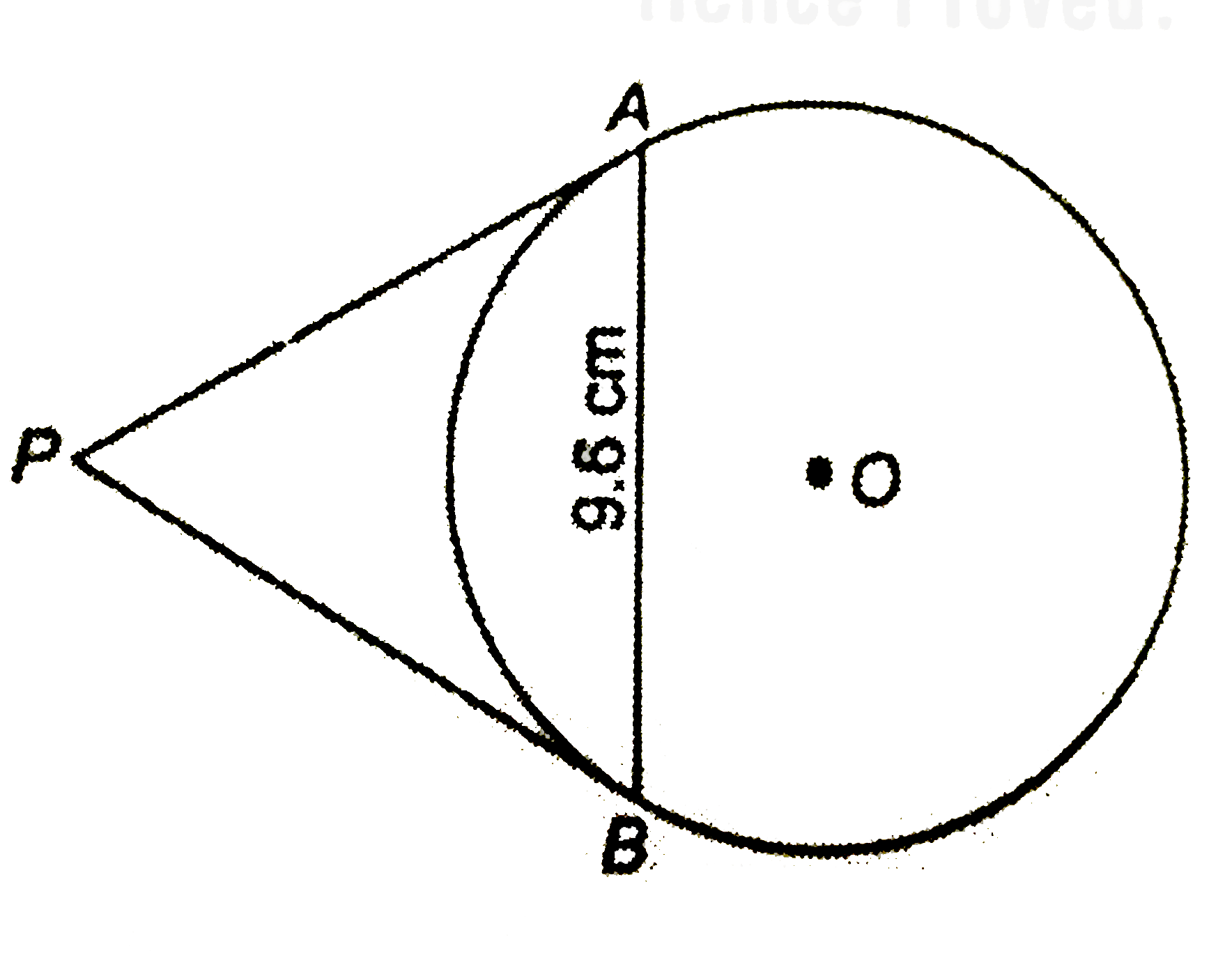
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
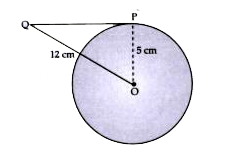
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ =12 cm . Length PQ is :
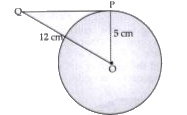
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
View SolutionIf a chord of a circle of radius 5 cm is a tangent to another circle of radius 3 cm, both the circles being concentric, then the length of the chord is
View Solution
