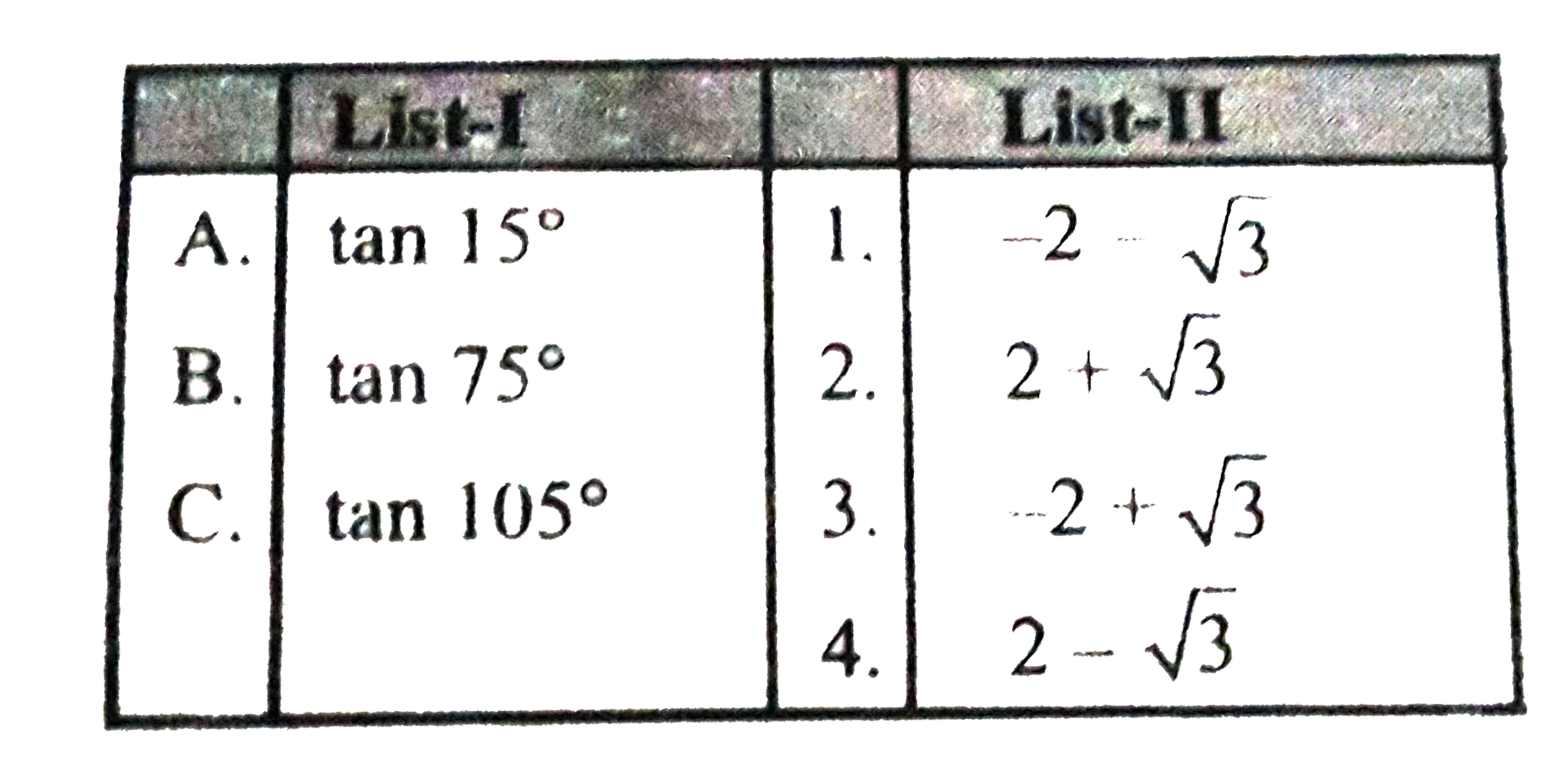AB and CD are two chords of a circle meeting externally at P. Then, which of the following is/are correct?
I.PAxPD = PCxPB. traingle PAC and traingle PDB are similar.
Select the correct answer using the codes given below.
Only I
Only II
Both I and II
Neither I nor II
The correct Answer is:D
To solve the problem, we need to analyze the statements given about the two chords AB and CD that meet externally at point P.
1. Understanding the Chords and Point of Intersection:
- We have two chords, AB and CD, intersecting externally at point P.
- The segments created by the intersection are PA, PB, PC, and PD.
2. Analyzing the First Statement:
- The first statement claims that PA×PD=PC×PB.
- According to the theorem of intersecting chords, when two chords intersect, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.
- Therefore, we can express this as:
PA×PB=PC×PD
- Rearranging gives us:
PA×PD=PC×PB
- This confirms that the first statement is correct.
3. Analyzing the Second Statement:
- The second statement claims that triangles PAC and PDB are similar.
- For two triangles to be similar, they must have equal corresponding angles.
- Here, we note that:
- Angle PAC is not necessarily equal to angle PDB unless the lines AC and BD are parallel.
- Since we do not have any information suggesting that AC is parallel to BD, we cannot conclude that the triangles are similar.
- Thus, the second statement is incorrect.
4. Conclusion:
- The first statement is correct: PA×PD=PC×PB.
- The second statement is incorrect: triangles PAC and PDB are not necessarily similar.
- Therefore, the correct answer is that only the first statement is true.
Final Answer:
- The correct answer is: Only the first statement is correct.
- We have two chords, AB and CD, intersecting externally at point P.
- The segments created by the intersection are PA, PB, PC, and PD.
- The first statement claims that PA×PD=PC×PB.
- According to the theorem of intersecting chords, when two chords intersect, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.
- Therefore, we can express this as:
PA×PB=PC×PD
- Rearranging gives us:
PA×PD=PC×PB
- This confirms that the first statement is correct.
- The second statement claims that triangles PAC and PDB are similar.
- For two triangles to be similar, they must have equal corresponding angles.
- Here, we note that:
- Angle PAC is not necessarily equal to angle PDB unless the lines AC and BD are parallel.
- Since we do not have any information suggesting that AC is parallel to BD, we cannot conclude that the triangles are similar.
- Thus, the second statement is incorrect.
- The first statement is correct: PA×PD=PC×PB.
- The second statement is incorrect: triangles PAC and PDB are not necessarily similar.
- Therefore, the correct answer is that only the first statement is true.
- The correct answer is: Only the first statement is correct.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
Two chords AB and CD of a circle intersects each other at P. which of the following is correct?
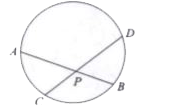 AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PD
AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PDMatch 1list I with list II and select the correct answer using the code given below
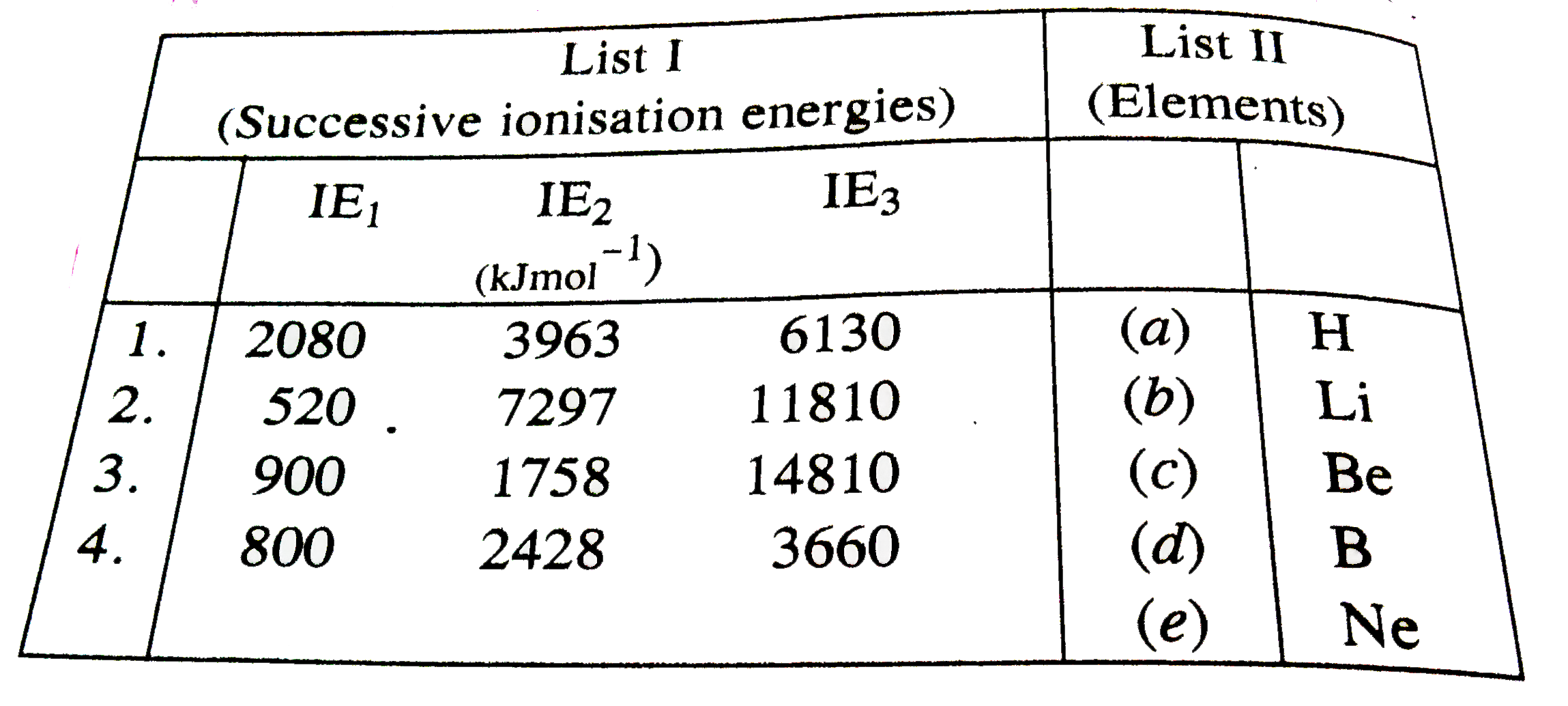 A1.c,2. b,3.d ,4.eB1. a,2. c, 3. b, 4.dC1. d, 2. a, 3. b , 4. dD1. e,2. b,3. c,4. d
A1.c,2. b,3.d ,4.eB1. a,2. c, 3. b, 4.dC1. d, 2. a, 3. b , 4. dD1. e,2. b,3. c,4. dMatch the following and select the correct answer by using codes given below.
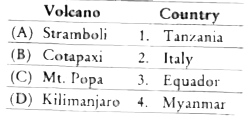 AABCD1234BABCD2134CABCD2314DABCD2341
AABCD1234BABCD2134CABCD2314DABCD2341
Match Column-I with Column-I and select the correct answer using the codes given below :

View SolutionMatch List I with List II and select the correct answer using the code given below:


View SolutionMatch List I with List II and select the correct answer using the code given below:
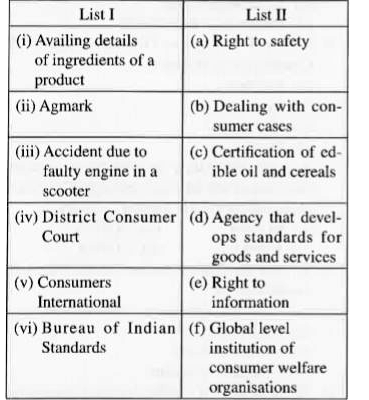
View SolutionMatch Column I with Column II and select the correct answer using the codes given below

View SolutionMatch Column-I with Column-I and select the correct answer using the codes given below :

View Solution