In the adjoining figure, the bisectors of of a quadrilateral ABCD meet CD and AB produced at P and Q respectively.
Proove that
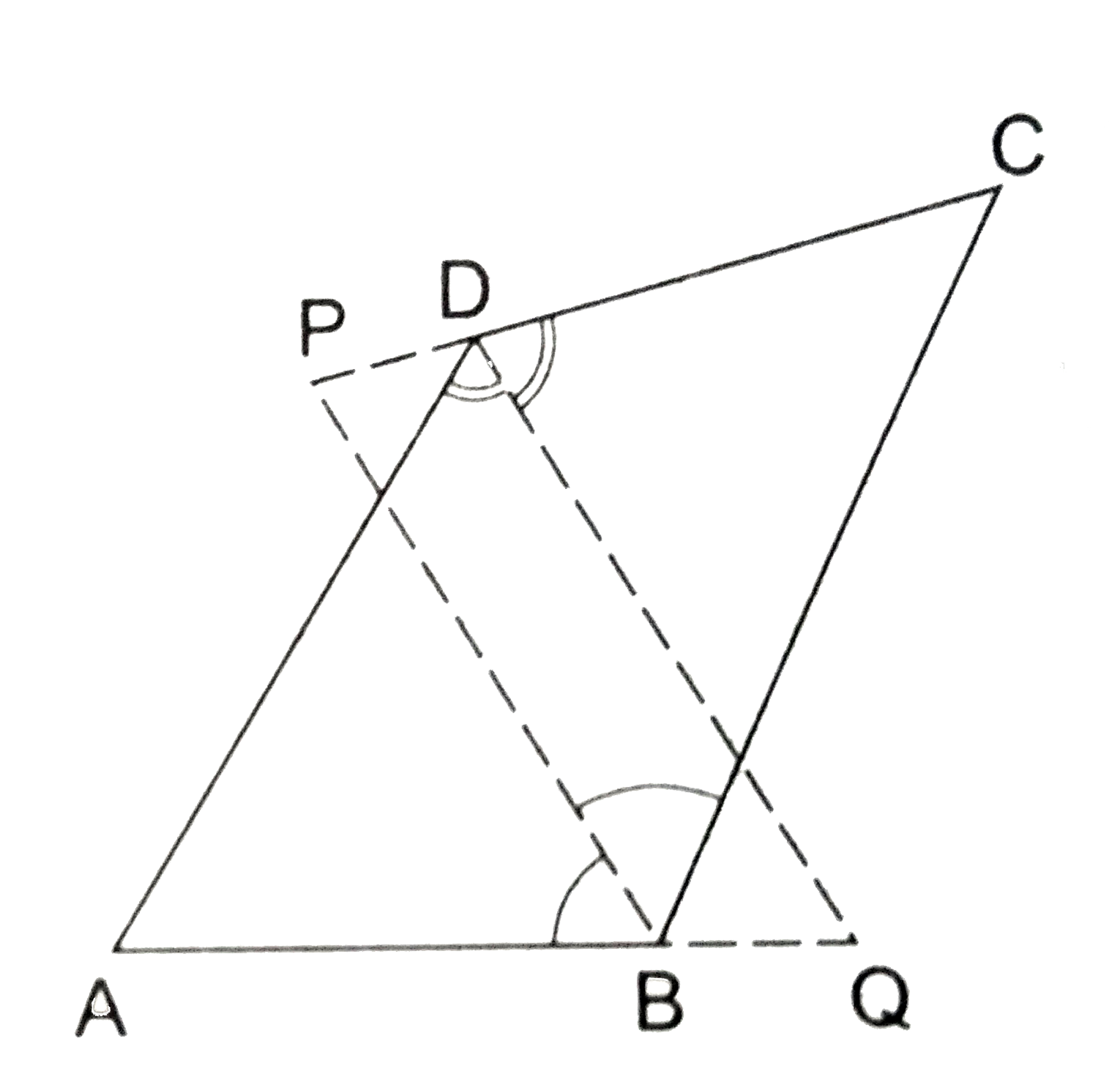
In we have
…(i)
In , we have
...(ii)
Adding (i) and (ii), we get
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
In the figure, bisectors of ∠Band∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=1/2(∠ABC+∠ADC)
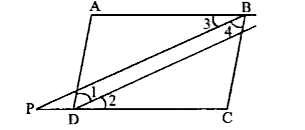
Given: In the given figure, bisectors of ∠Band∠D of a quadrilateral ABCD meet CD and AB produced at P and Q respectively.
To prove: ∠P+∠Q=12(∠ABC+∠ADC)
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
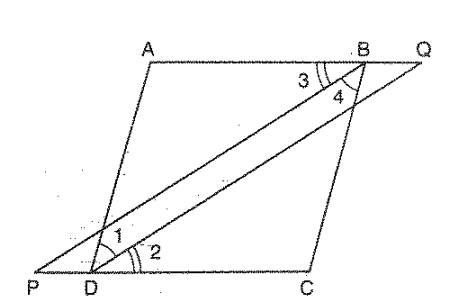
View Solution
Knowledge Check
If the bisector of the angles A and B of a quadrilateral ABCD meet at O, then ∠AOB is equal to:
A∠C+∠DB12(∠C+∠D)C12∠C+13∠DD13∠C+12∠DIf the bisector of the angles A and B of a quadrilateral ABCD meet at O, then ∠AOB is equal to:
A∠C+∠DB12(∠C+∠D)C12∠C+13∠DD13∠C+12∠D
In Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at Pand Q respectively. Prove that : ∠P+∠Q=12(∠ABC+∠ADC)
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that
∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn triangle ABC, AD and aEarn ABCD is a rhombus, AB is produced In the figure bisector of B and D of quadrilateral ABCD meet CO and AB produced and Q respectively. Prove that angle P t angle Q (angle ABC t le ADC). A
View SolutionIn the adjoining figure, p∣∣q. Find the unknown angles.

View SolutionBisectors of angles A and D of a quadrilateral ABCD meet at P. Prove that ∠APD=12(∠B+∠C)
View Solution
