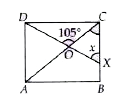
In the given figure, ABCD is a square. A line segment DX cuts the side BC at X and the diagonal AC at O such that ∠COD=105∘and∠OXC=x. The value of x is

Video Solution
Text Solution
The angle of a square are bisected by the diagonals.
∴∠OCX=45∘[∵∠DCB=90∘andCA bisects ∠DCB].
Also, ∠COD+∠COX=180∘ (linear pair)
⇒105∘+∠COX=180∘⇒∠COX=(180∘−105∘)=75∘.
Now, in △COX, we have
∠OCX+∠COX+∠OXC=180∘
⇒45∘+75∘+∠OXC=180∘⇒∠OXC=(180∘−120∘)=60∘.
Hence, x=60.
|
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Exercise 10 A
Explore 10 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXERCISE 10B
Explore 27 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Matching of Columns:
Explore 2 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD is a square. A line segment DX cuts the side BC at X and the diagonal AC at O such that <COD=105∘ and <OXC=x. The value of x is
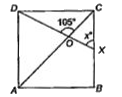 A40∘B60∘C80∘D85∘
A40∘B60∘C80∘D85∘In the given figure, ABCD is a square. Find x.
 A60∘B120∘C100∘D110∘
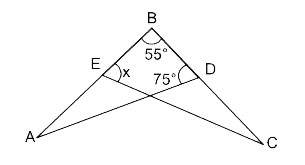
A60∘B120∘C100∘D110∘In the given figure, ABCD is a quadrilateral, the line segments bisecting ∠Cand∠D meet at E. Then 2∠CED is equal to
 A∠A+∠BB∠A+∠CC∠B+∠DD∠C+∠D
A∠A+∠BB∠A+∠CC∠B+∠DD∠C+∠D
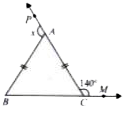
In the figure AB=AC,∠ACM=140∘and∠PAB=x. Find the value of x.
View SolutionIn the given figure , if AB=BC and ∠A=∠C then find the value of x
View SolutionIn the given figure ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC=55∘and∠BAC=45∘, find ∠BCD.
View SolutionIn the given figure, OPOR is a square. A circle drawn with centre O, cuts the square X and Y. Prove that QX=QY.
View SolutionIn the figure AB=AC angle BAD=30∘andAE=AD, then the value of x is
View Solution