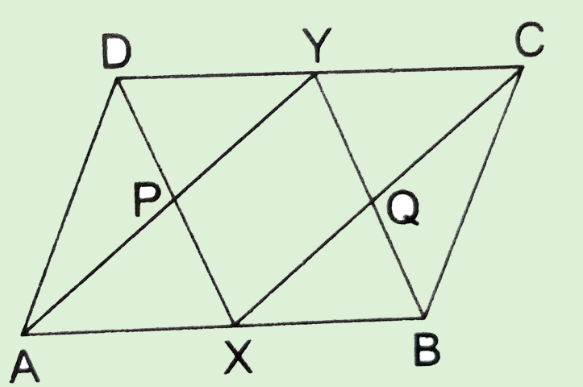
In the adjoining figure, ABCD is a parallelogram in which X and Y are the midpoints of AB and DC respectively. If AY and DX intersect in P while CX and BY intersect in Q, show that
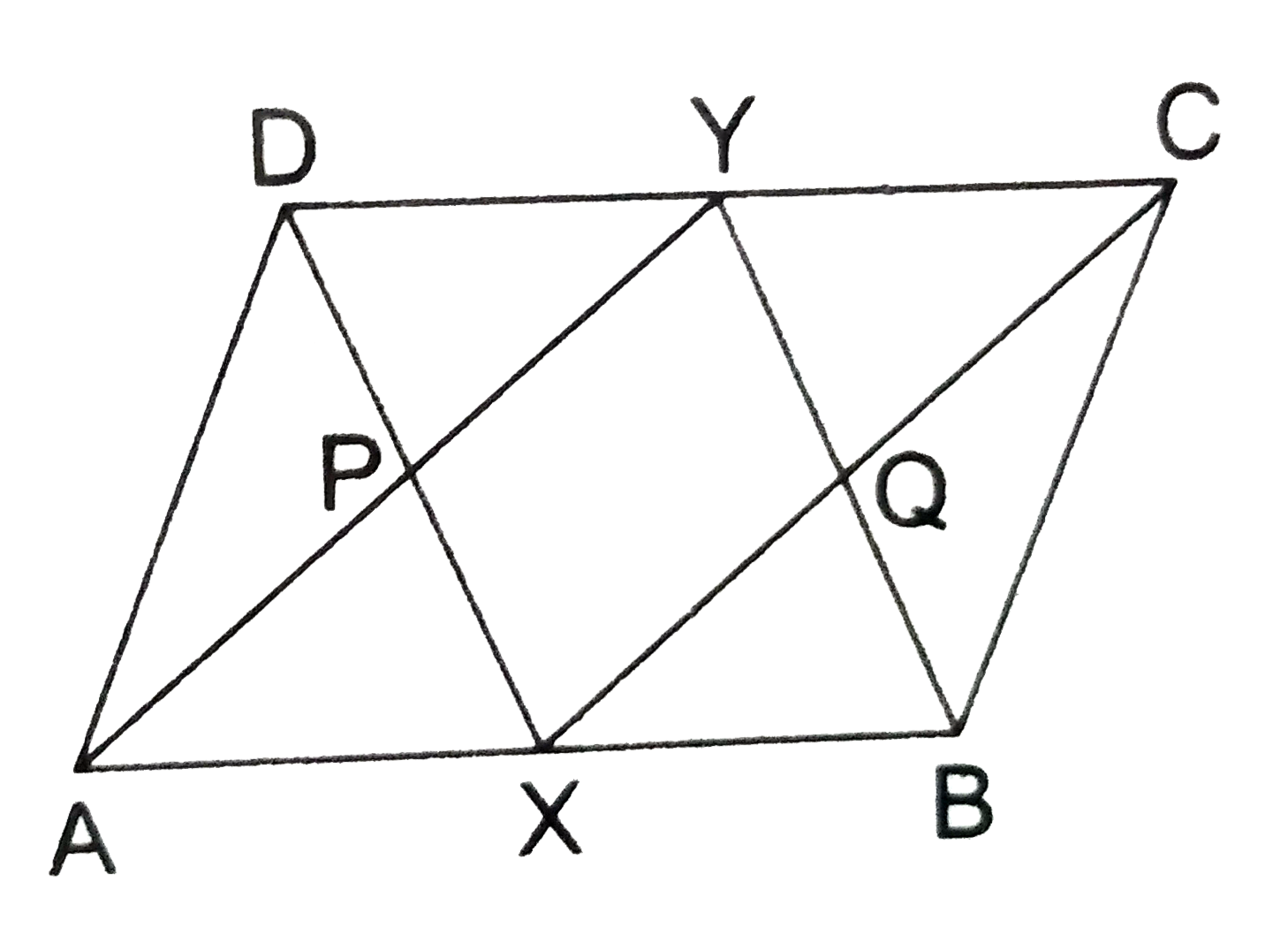
(i) quad. AXCY is a parallelogram,
(ii) quad. XBYD is a parallelogram,
(iii) quad. PXQY is a parallelogram.
AB||DC⇒AX||YC.
Also, AB=DC⇒12AB=12DC⇒AX=YC.
∴AX||YCandAX=YC⇒AXCY is a ||gm.
∴ AY||XC. In particualr, PY||XQ.
Again, AB||DC ⇒ XB||DY.
Also, AB=DC⇒12AB=12DC⇒XB=DY.
∴XB||DY andXB=DY⇒XBYD is a ||gm.
∴ XD||BY. In particular, XP||QY.
Thus, PY||XQ and XP||QY.
∴ PXQY is a parallelogram.
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Exercise 10 A
Explore 10 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXERCISE 10B
Explore 27 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Matching of Columns:
Explore 2 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
ABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
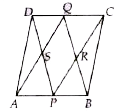
(i) APCQ is a parallelogram.
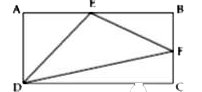
View SolutionIn the given figure ABCD is a parallelogram in which AB||CD and E and F are the mid points of AB and BC respectively. What is the area of ∠BEF?
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

DPBQ is a parallelogram
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

PSQR is a parallelogram.
View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram.(ii) DPBQ is a parallelogram.(iii) PSQR is a parallelogram
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH.
View SolutionABCD is a parallelogram. P and R are the midpoints of DC and BC respectively. The line PR intersects the diagonal AC at Q . The distance CQ will be equal to
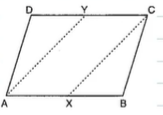
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.

View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
View Solution

