Question

Prove that any line segment drawn from the vertex of a triangle to the base is bisected by the line segment joining the midpoints of the other sides of the triangle.

Explanation

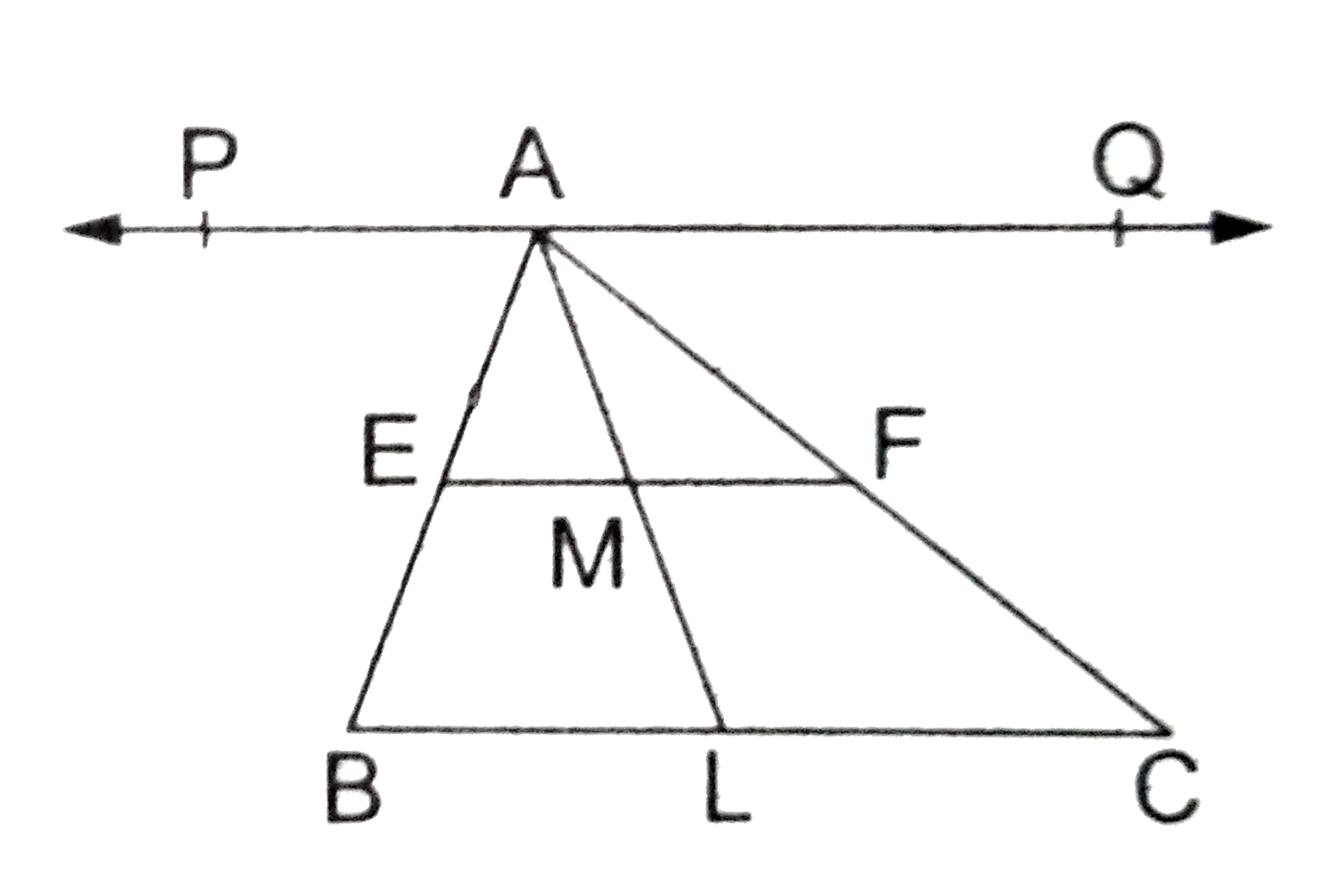
Let `triangle`ABC be a given triangle in which E and F are F are the midpoints of AB and AC respectively. Let AL be a line segment drawn from vertex A to the base BC, meeting BC at L and EF at M.
We have to show AM = ML.
Through A, draw PAQ||BC.
In `triangle`ABC, E and F being the midpoints of AB and AC respectively, we have EF||BC.
Now, PAQ, EF and BC are three parallel lines such that the intercepts AE and EB made by them on transversal AEB are equal.
`therefore ` the intercepts AM and ML made by them on transversal AML must be equal.
Hence, AM = ML.