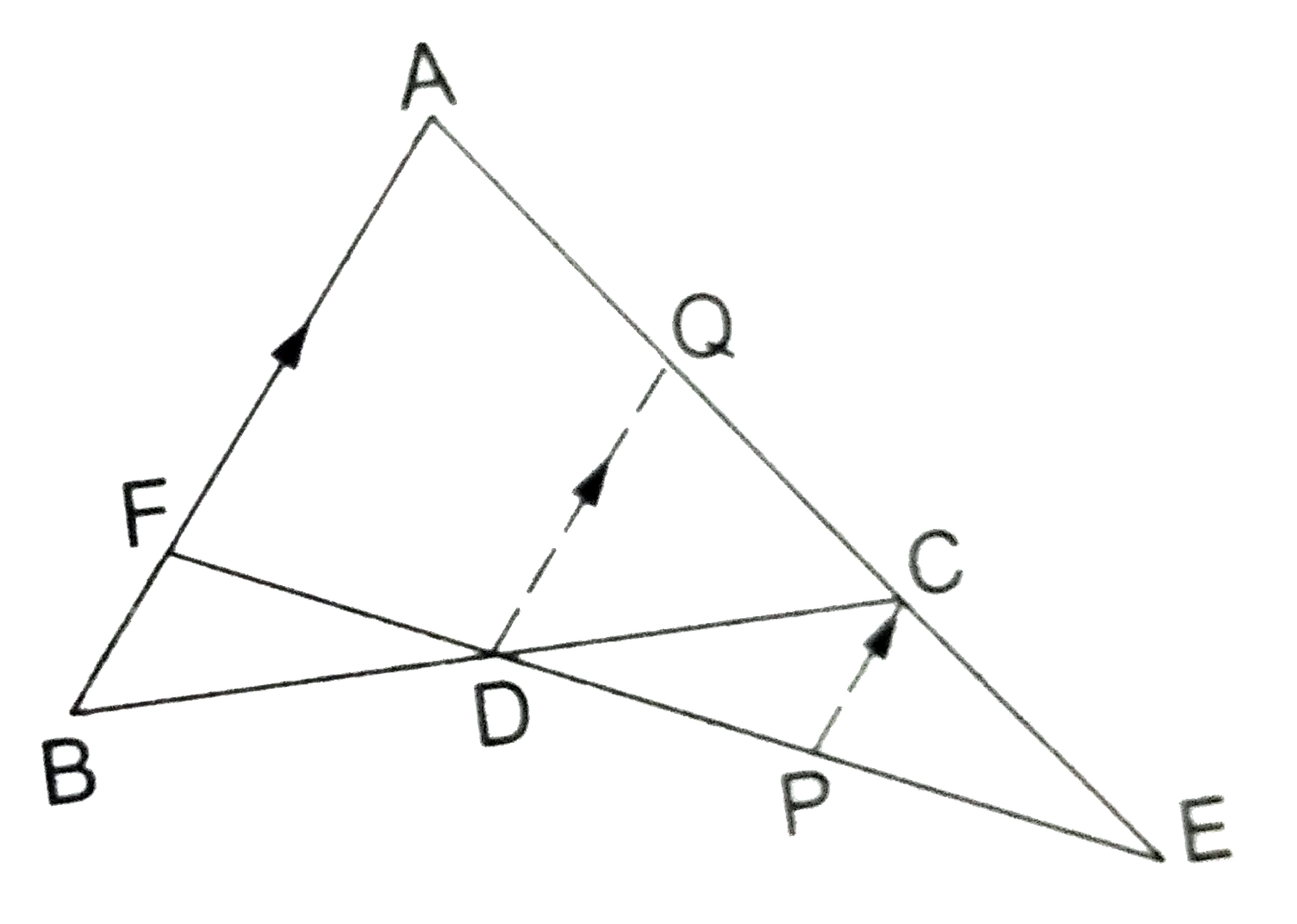
In the adjoining figure, the side AC of △ABC is produced to E such that CE=12AC. If D is the midpoint of BC and ED produced meets AB at F, and CP, DQ are drawn parallel to BA, prove that FD=13FE.
Video Solution
Text Solution
In △ABC, D is the midpoint of BC and DQ||BA.
∴ Q is the midpoint of AC.
∴AQ=QC.
Now, FA||DQ||PC, and AQC is the transversal such that AQ = QC and FDP is the other transversal on them.
∴FD=DP ...(i) (by intercept theorem).
Now, EC=12AC=QC.
∴ in △EQD, C is the midpoint of EQ and CP||DQ.
∴ P must be the midpoint of DE.
∴DP=PE. ...(ii)
Thus, FD=DP=PE [form (i) and (ii) ].
Hence, FD=13FE.
|
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Exercise 10 A
Explore 10 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXERCISE 10B
Explore 27 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Matching of Columns:
Explore 2 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
Knowledge Check
The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
In the given figure, the side AC of ΔABC is produced to E such that CE = FAC. If D is the midpoint of BC and ED produced meets AB at F and CP, DQ are drawn parallel to BA, then FD=
 A12FEB13EFC2FEDFE
A12FEB13EFC2FEDFEIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
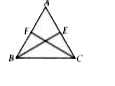 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of theseIn the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
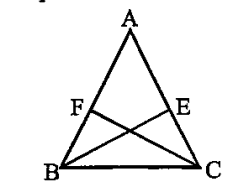 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
In ΔABC, E is the midpoint of the median AD. BE produced meets AC at F. Prove that AF=(13)AC
View SolutionIn the given figure, side BC of △ABC is produced to D and CE||BA. If ∠BAC=50∘,then ∠ACE = ……
View SolutionIf a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
View SolutionIn the adjoining figure, ABCD is a paralogram. The side AB is produced to P such that AB=BP and the side AD is produced to Q such that AD = DQ. Prove that CP = CQ.
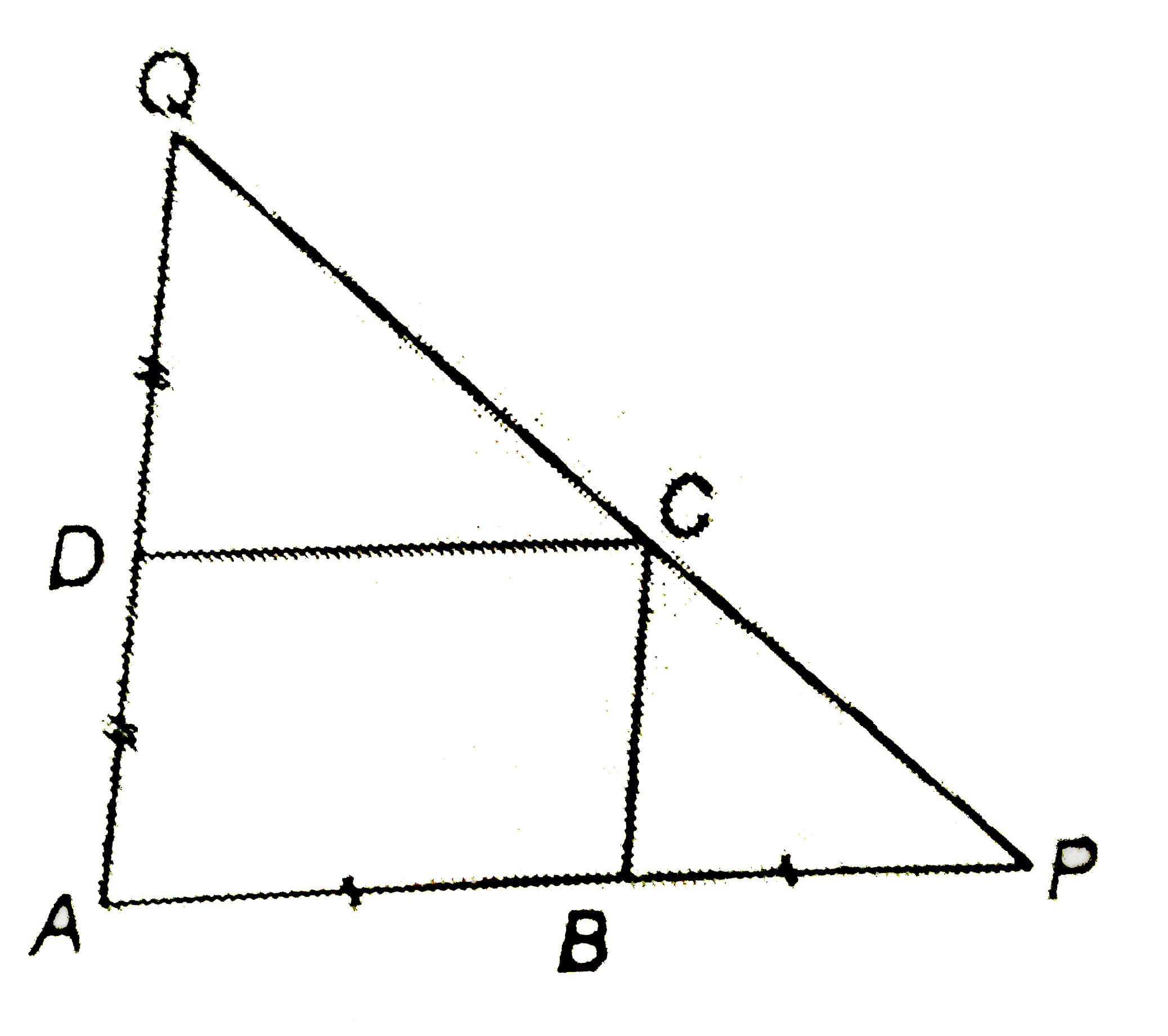
View SolutionΔABC,AB=AC and BA is produced to D such that AC = AD. Then the ∠BCD is
View Solution