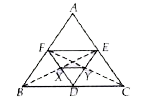
In the given figure, D, E and F are the midpoints of the sides BC, CA and AB of $Δ A B C . B E$ bisect DF at X while CF bisect DE at Y, then BC = a XY. Find a.

Video Solution

Text Solution

Verified by Experts

In $△ A B C$ , F and E are the midpoints of AB and AC respective
$∴ FE||BC and F E = \frac{1}{2} B C = B D .$
$∴ FE||BD and F E = B D .$
So, BDEF is a parallelogram whose diagonals BE and DF intersect each other at X.
$∴$ X is the midpoint of DF.
Similarly, Y is the midpoint of DE.
Thus, in $△ D E F$ , X and Y are the midpoints of DF and DE respectively.
So, XY||FE and $X Y = \frac{1}{2} F E = \frac{1}{2} \times \frac{1}{2} B C = \frac{1}{4} B C .$

Updated on:21/07/2023

In a triangle ABC, D, E and F are the mid-points of the sides BC, CA and AB, respectively. BE and DF intersect at X. DE and CF intersect at Y. Find $X Y = ?$
A) $\frac{1}{2} B C$
B) $\frac{1}{4} B C$
C) $\frac{1}{3} B C$
D) $\frac{2}{3} B C$
A $\frac{1}{2} B C$
B $\frac{1}{4} B C$
C $\frac{1}{3} B C$
D $\frac{2}{3} B C$
Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0
B0
C2
DNone of these
ABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of $Δ A B C and Δ D E F$ is :
A $20 %$
B $25 %$
C $50 %$
D $40 %$