if D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OF
Since, D is the mid-point of Bc, therefore by section formula, we have
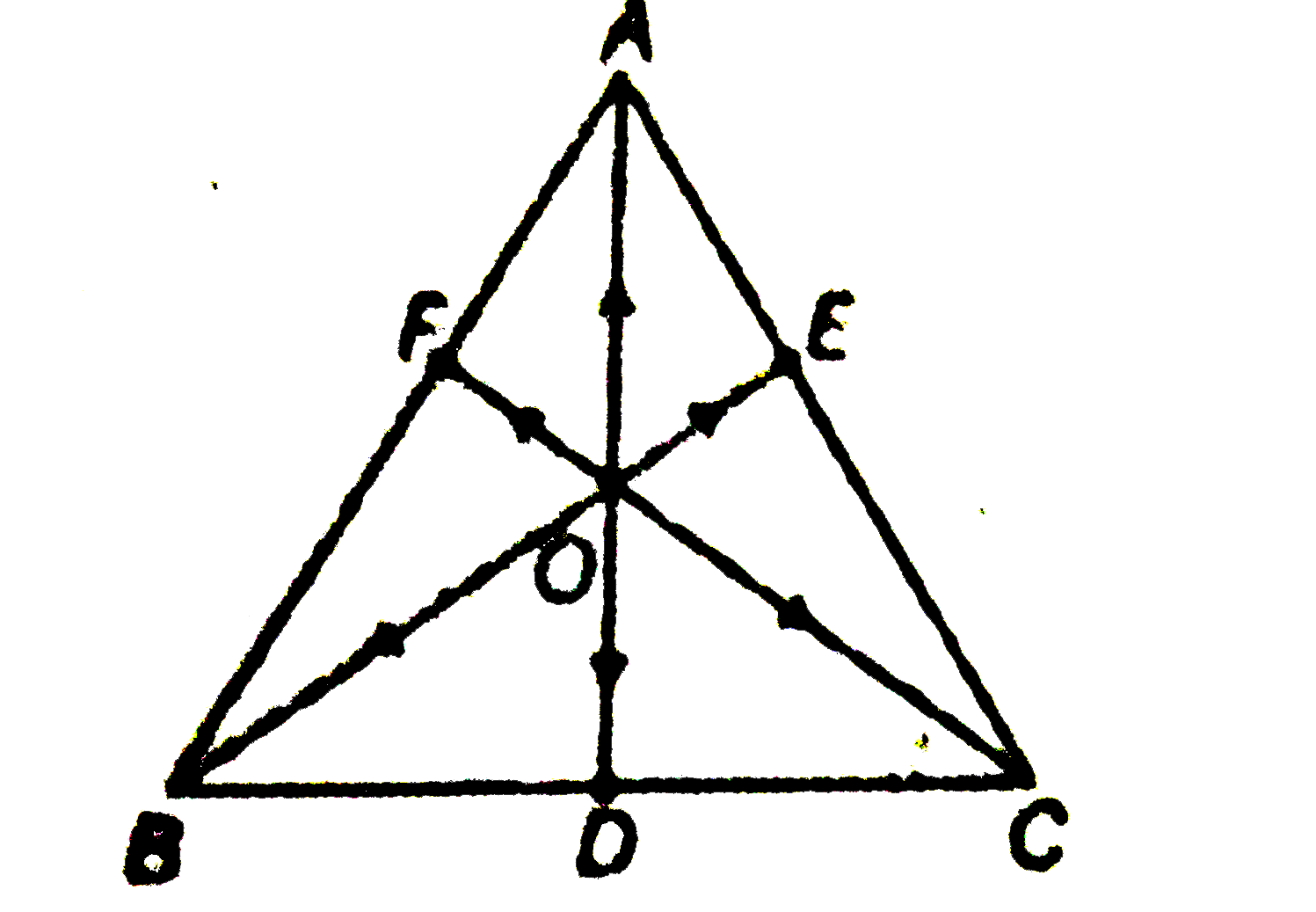
OD=OB+OC2
⇒OB+OC=2OD . . . (i)
Similarly, OC+OA=2OE . . (ii)
and OB+OA=2OF . . . (iii)
On adding Eqs. (i), (ii) and (iii), we get
2(OA+OB+OC)=2(OD+OE+OF)
⇒OA+OB+OC=OD+OE+OF Hence proved.
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 1
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 2
Explore 17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
If D E and F be the mid ponts of the sides BC, CA and AB respectively of the △ABC and O be any point, then prove that −−→OA+−−→OB+−−→OC=−−→OD+−−→OE+−−→OF
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View Solution
Knowledge Check
If D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OAAA. a zero vectorBB. a unit vectorCC. 0DD. none of theseIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CFIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
A→BE+→CFB→BE−→CFC→CF−→BED−→BE−→CF
If D(3,-2) , E(-3,1) and F(4,-3) are the mid-points of the sides BC, CA and AB respectively of ΔABC , find the co-ordinates of point A , B and C .
View SolutionIf D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
View Solution

