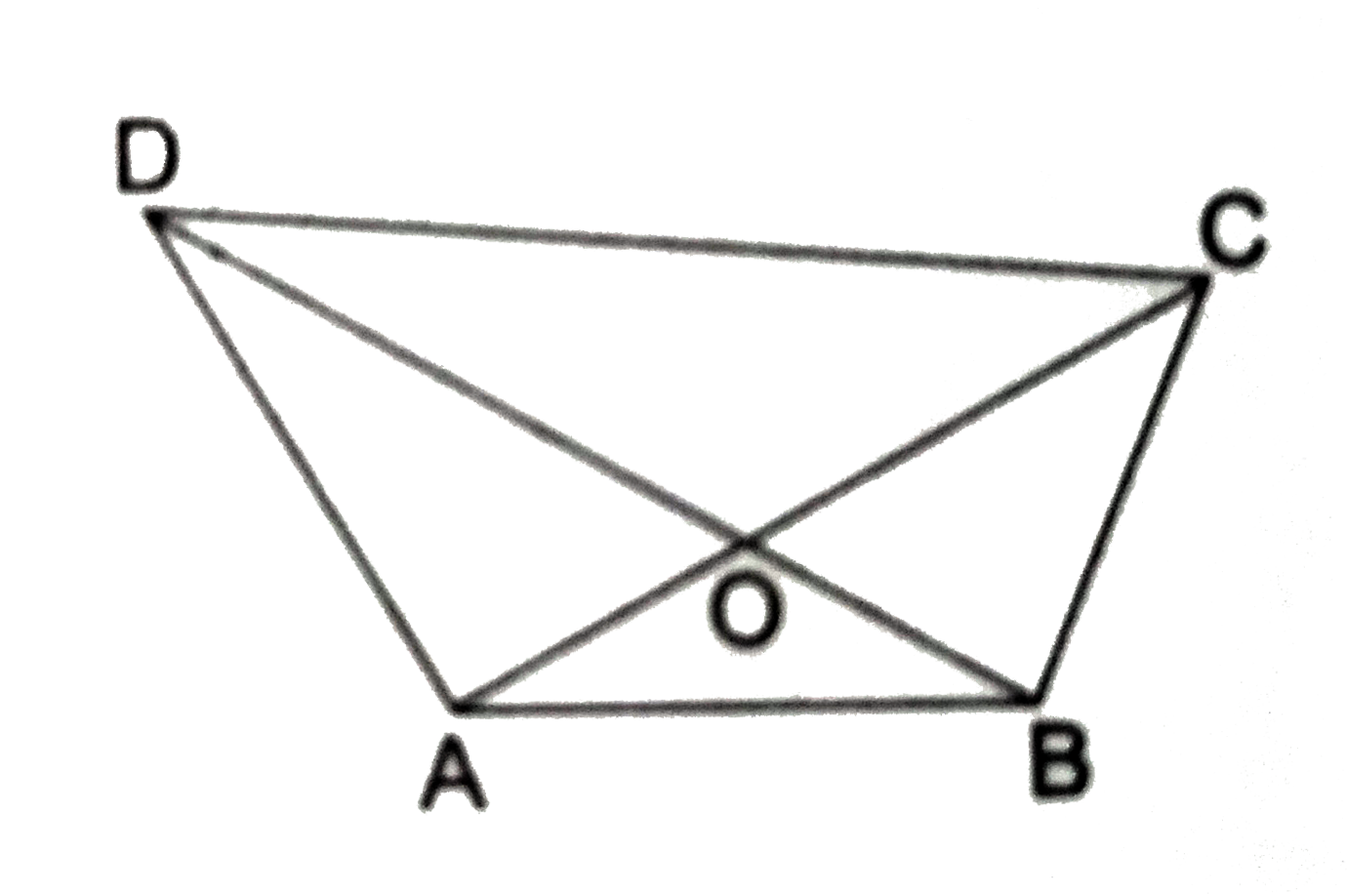
If ABCD is a quadrilateral whose diagonals AC and BD intersect at O, prove that
(i) (AB+BC+CD+DA)>(AC+BD),
(ii) (AB+BC+CD+DA)<2(AC+BD).
Video Solution
Text Solution
(i) We know that the sum of any two sides of a triangle is greater than the third.
In △ABC, we have AB+BC>AC.
In △ACD, we have CD+DA>AC.
In △BCD, we have BC+CD>BD.
In △ABD, we have DA+AB>BD.
adding these inequalities, we get
2(AB+BC+CD+DA)>2(AC+BD).
∴AB+BC+CD+DA>AC+BD
(ii) In △AOB, we have OA+OB>AB.
In △BOC, we have OB+OC>BC.
In △COD, we have OC+OD>CD.
In △DOA, we have OD+OA>DA.
Adding these inequalities, we get
2(OA+OC)+2(OB+OD)>AB+BC+CD+DA
⇒2(AC+BD)>AB+BC+CD+DA
⇒AB+BC+CD+DA<2(AC+BD).
|
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
ABCD is a quadrilateral whose diagonals are AC and BD. Which one of the following is correct?
A−−→BA+−−→CD=−−→AC+−−→DBB−−→BA+−−→CD=−−→BD+−−→CAC−−→BA+−−→CD=−−→AC+−−→BDD−−→BA+−−→CD=−−→BC+−−→ADABCD is a quadrilateral whose diagonals are AC and BD. Which one of the following is correct?
AA. −−→BA+−−→CD=−−→AC+−−→DBBB. −−→BA+−−→CD=−−→BD+−−→CACC. −−→BA+−−→CD=−−→AC+−−→BDDD. −−→BA+−−→CD=−−→BC+−−→ADIn a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)
ABCD is a quadri,aterial prove that (AB+BC+CD+DA)>(AC+BD)

View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)

View SolutionIn a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionIn a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
View Solution

