In the adjoining figure, ABCD is a parallelogram and X, Y are the points on the diagonal BD such that DX = BY. Prove that
(i) CXAY is a parallelogram,
(ii) △ADX≅△CBYand△ABY≅△CDX,and
(iii) AX=CYandCX=AY.
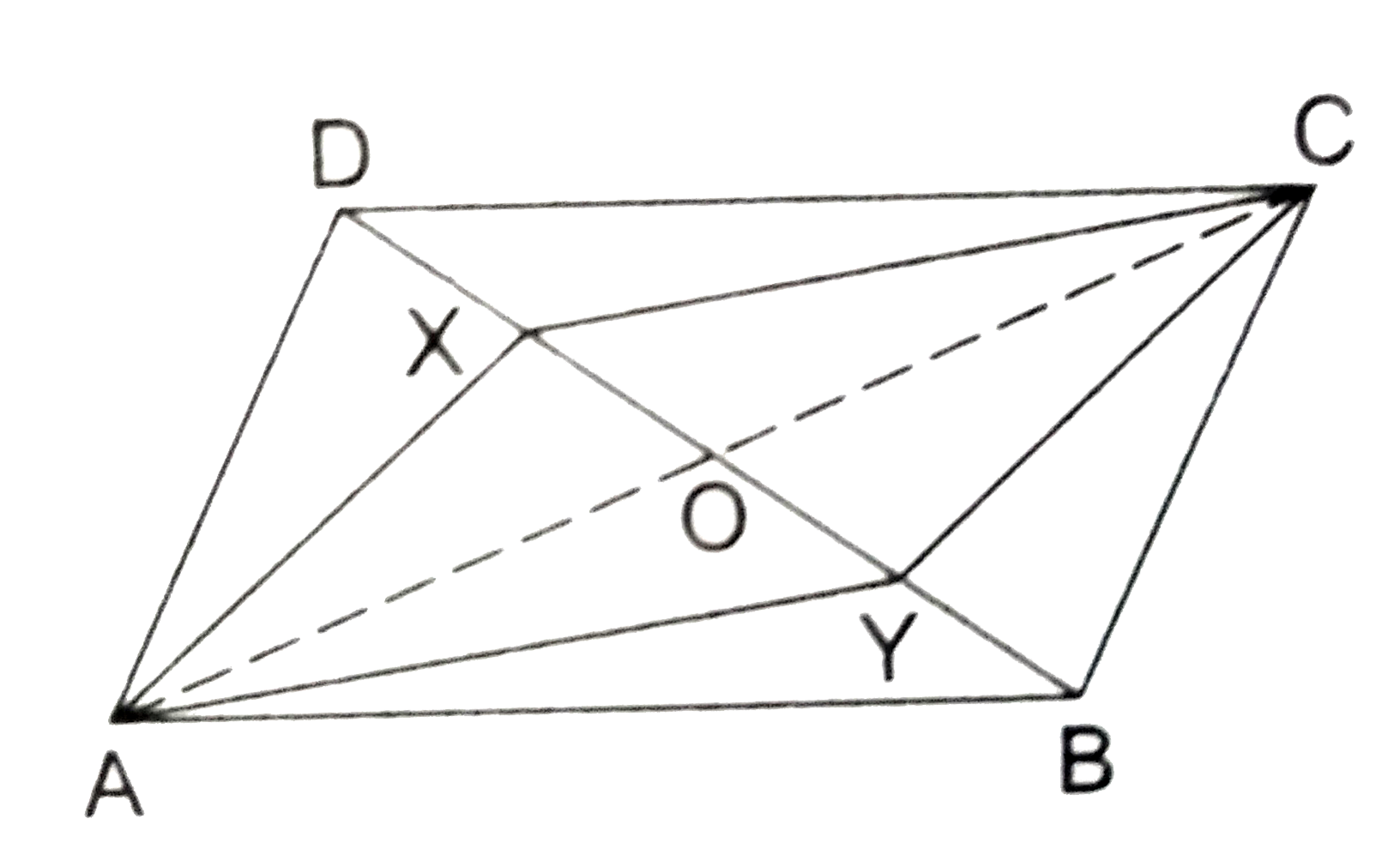
(i) Join AC , meeting BD at O.
Since the diagonals of a parallelogram bisect each other,
we have OA = OC and OD = OB.
Now, OD = OB and DX = BY
⇒OD−DX=OB−BY⇒OX=OY.
Now, OA = OC and OX = OY.
CXAY is a quadrilateral whose diagonals bisect each other.
∴CXAYisa∣∣gm.
(ii) and (iii) in △ADXandCBY, we have
AD=BC (opp. sides of a || gm)
∠ADX=∠CBY (alt. interior ∠)
DX=BY (given)
∴△ADX≅△CBY (SAS- criterion).
And so, AX=CY (c.p.c.t.).
Similarly, △ABY≅△CDX and so CX=AY(c.p.c.t.).
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
In the given figure, ABCD is a parallelogram. Find the area of ΔAED
View SolutionThe given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN. Prove that:
View SolutionIn the adjoning figure, ABCD is a parallelogram. Prove that : area of ΔBPC= area of ΔDPQ

View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX = AY. Prove that CX = BY.
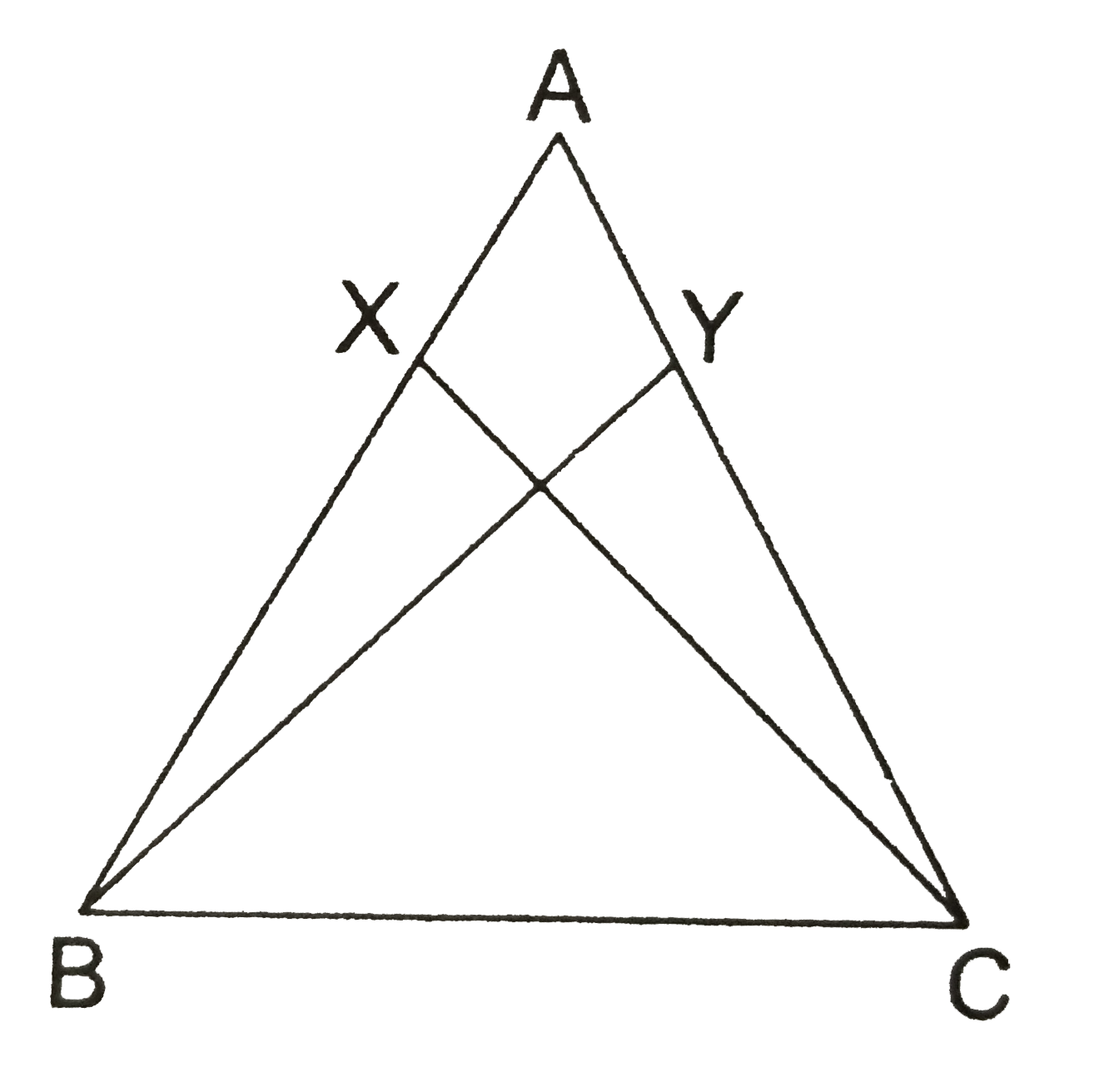
View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX=AY. Prove that CX=BY.
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
View SolutionTwo points X and Y lie on the diagonal BD of a parallelogram ABCD such that DX = BT. Prove that □AXCY is a parallelogram.
View SolutionIn the given figure, ABCD is a parallelogram whose area is 60cm2. Find the area of ΔACB
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that (BD+DC)<(AB+AC).
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
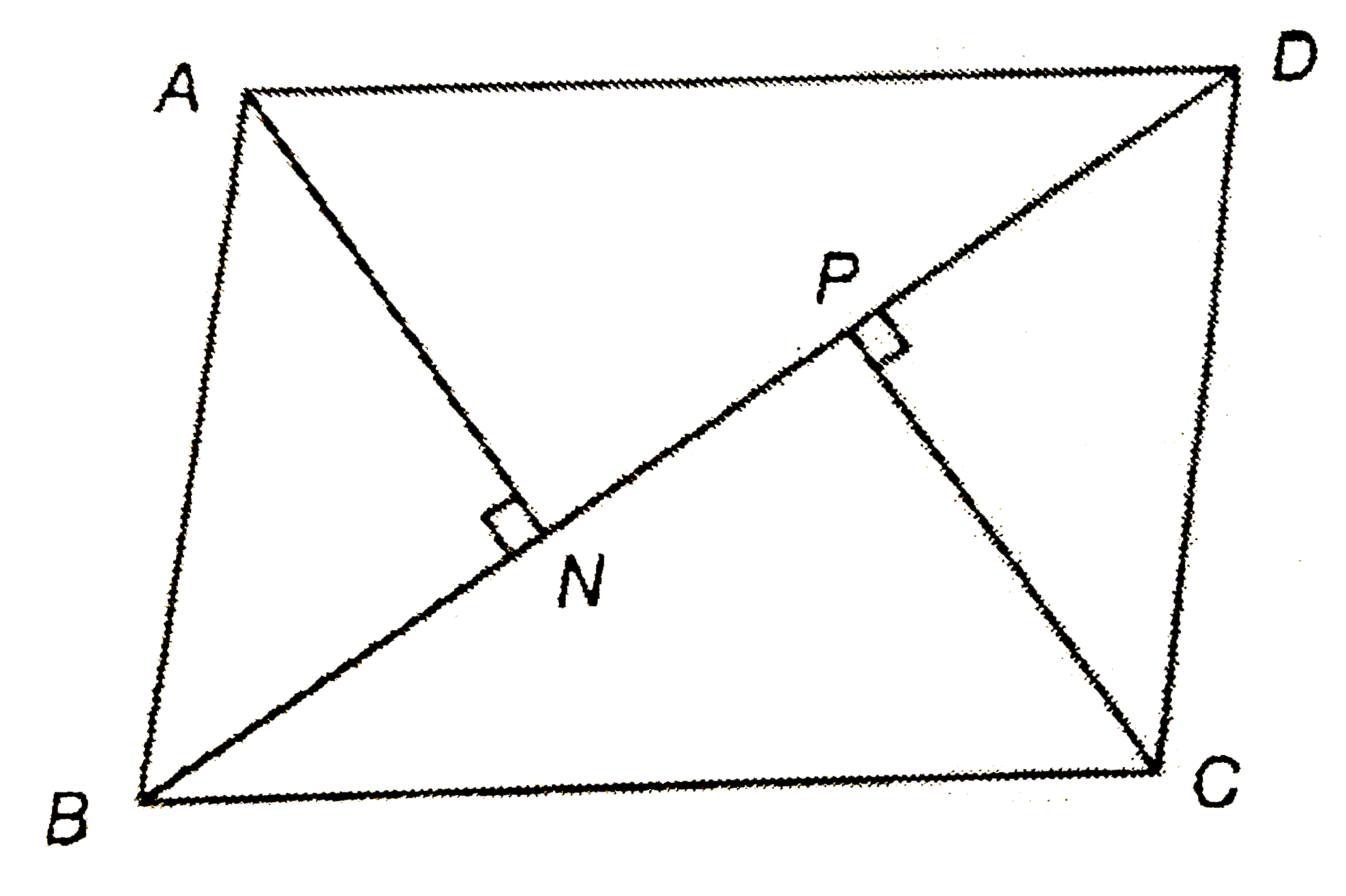
View Solution
