In the given figure, two circles intersect at P and Q.
If ∠A=80∘ and ∠D=84∘
calculate (i) ∠QBC and (ii) ∠BCP.
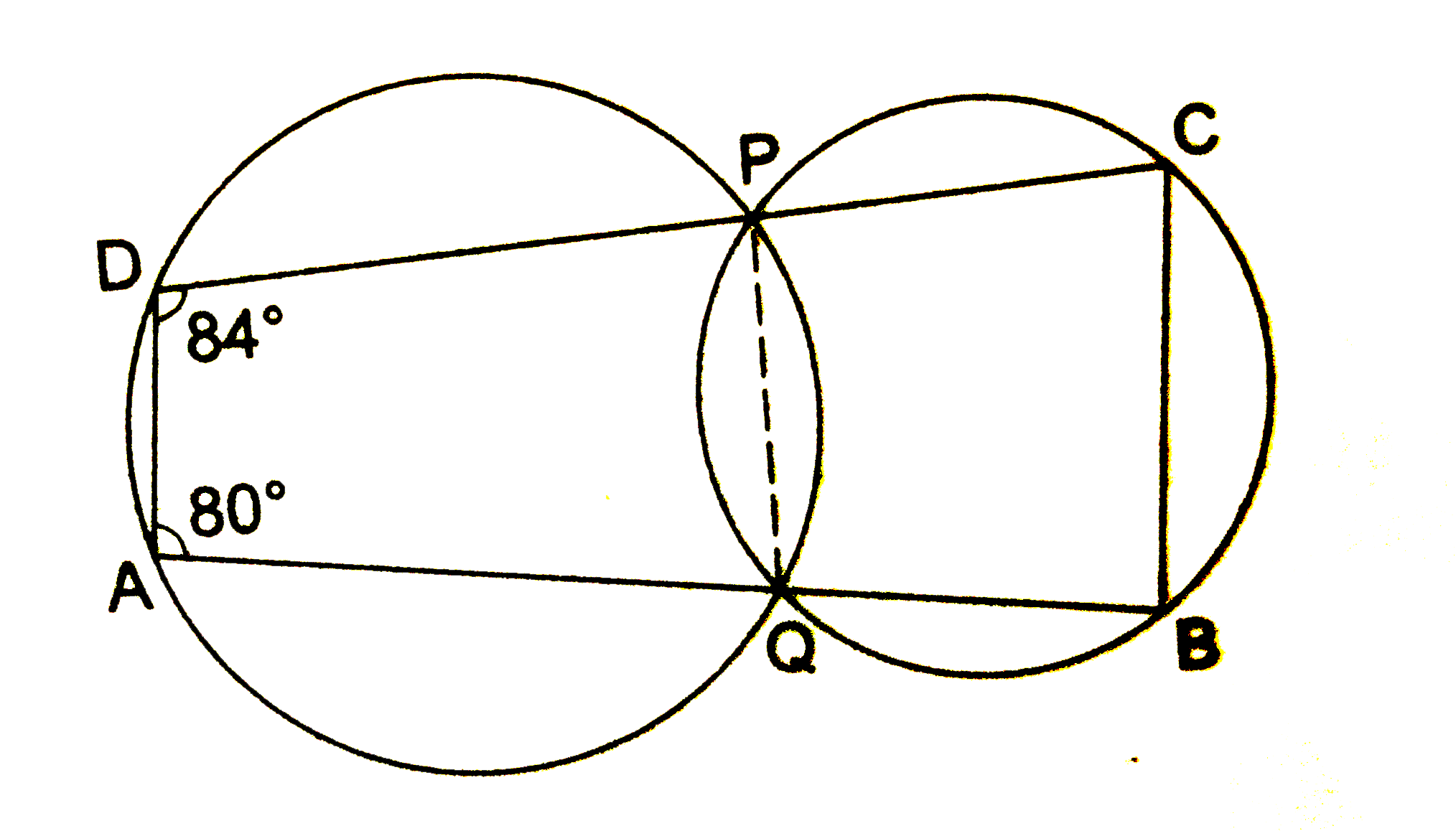
Join PQ
Now, quad . AQPD is cyclic.
⇒∠QAD+∠QPD=180∘
⇒80∘+∠QPD=180∘
⇒∠QPD=180∘−80∘=100∘
(i) The side CP of quad. QBCP is produced to D.
∴∠QBC=∠QPD=100∘ [ ext. ∠=int. opp. ∠]
(ii) Side AQ of cyclic quad. PDAQ is produced to B.
∴∠PQB=∠ADP=84∘ [ext. ∠= int. opp. ∠].
In the cyclic quad. QBCP, we have
∠PQB+∠BCP=180∘
⇒84∘+∠BCP=180∘
⇒∠BCP=180∘−84∘=96∘
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
Two circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
A120∘B135∘C160∘D180∘

In the figure, t intersects two parallel lines p and q. Find the angles of 4x−15∘and3x−15∘.
View SolutionIn the given figure O is the centre of the circle AC and BD intersects at P. If ∠AOB=100∘ and ∠DAP=30∘ then what is the value of ∠APB?
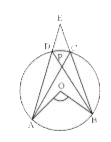
View SolutionTwo circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
View SolutionIn the given figure, two chords AC and BD of a circle intersect at E.If arcAB=arcCD, prove that : BE=EC and AE=ED
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionIn the given figure two circles touch each other at the point C. Prove that the common tangent at P and Q.
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.

View Solution