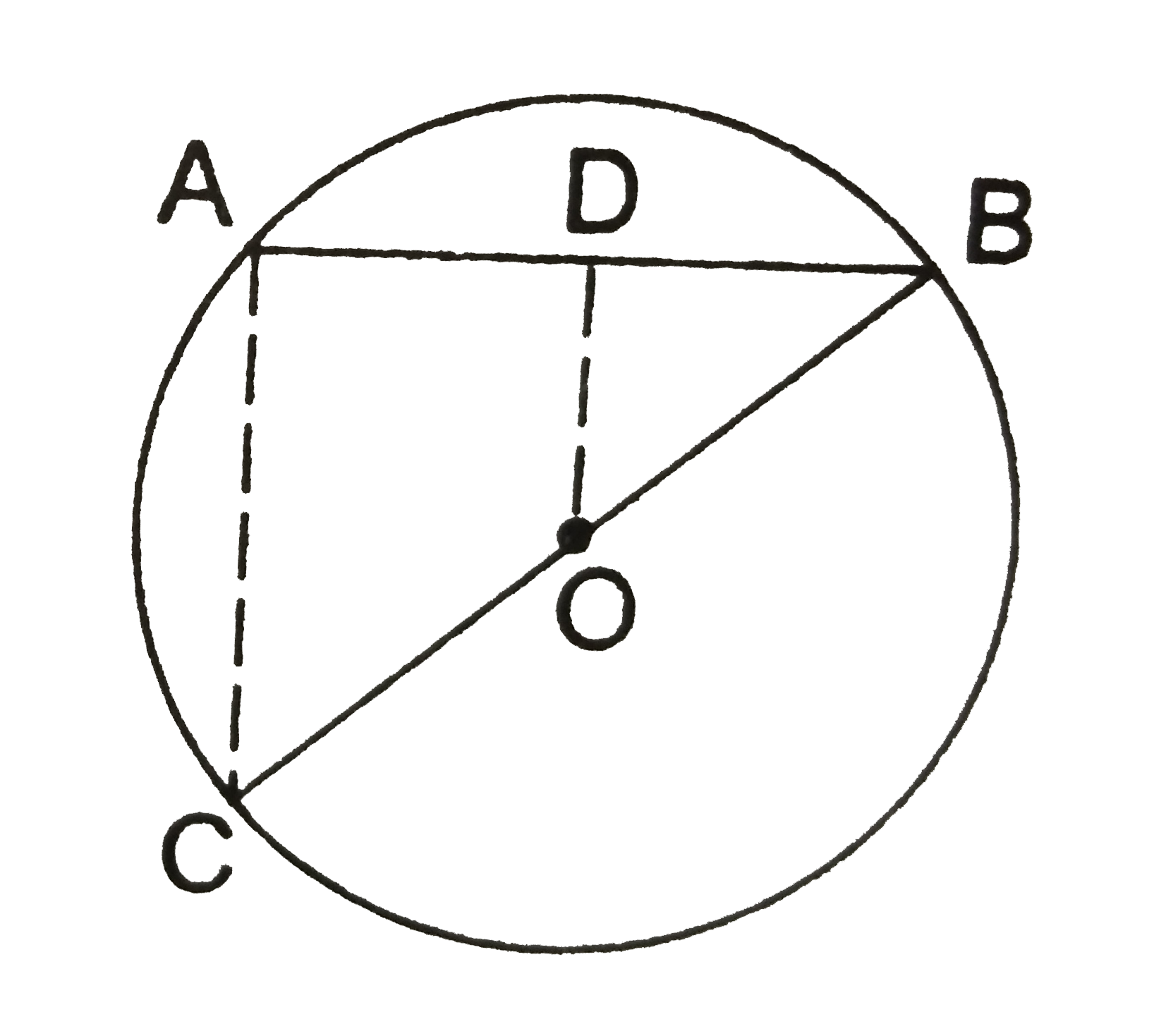
In the given figure, AB is a chord of a circle with centre O and BOC is a diameter . If OD ⊥ AB such that OD = 6 cm then AC=?
9cm
12cm
15cm
7.5cm
The correct Answer is:B
OD⊥AB⇒ D is the midpoint of AB.
Also, O is the midpoint of BC.
Now, in ΔBAC, D is the midpoint of AB and O is the midpoint of BC.
∴OD=12AC⇒AC=2×OD=(2×6)cm=12cm
Topper's Solved these Questions
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:Multiple Choice Questions (Mcq)
Explore 5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBook:RS AGGARWALChapter:BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONExercise:EXERCISE 17B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
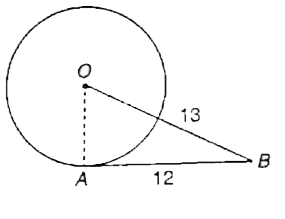 A6.5 cmB6 cmC5 cmDnone of these
A6.5 cmB6 cmC5 cmDnone of theseA ABC is inscribed in a circle with centre o and radius 5 cm and AC is a diameter of the circle. If AB = 8 cm, then BC = ......... cm.
A10B8C6D15
In the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionIn the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD
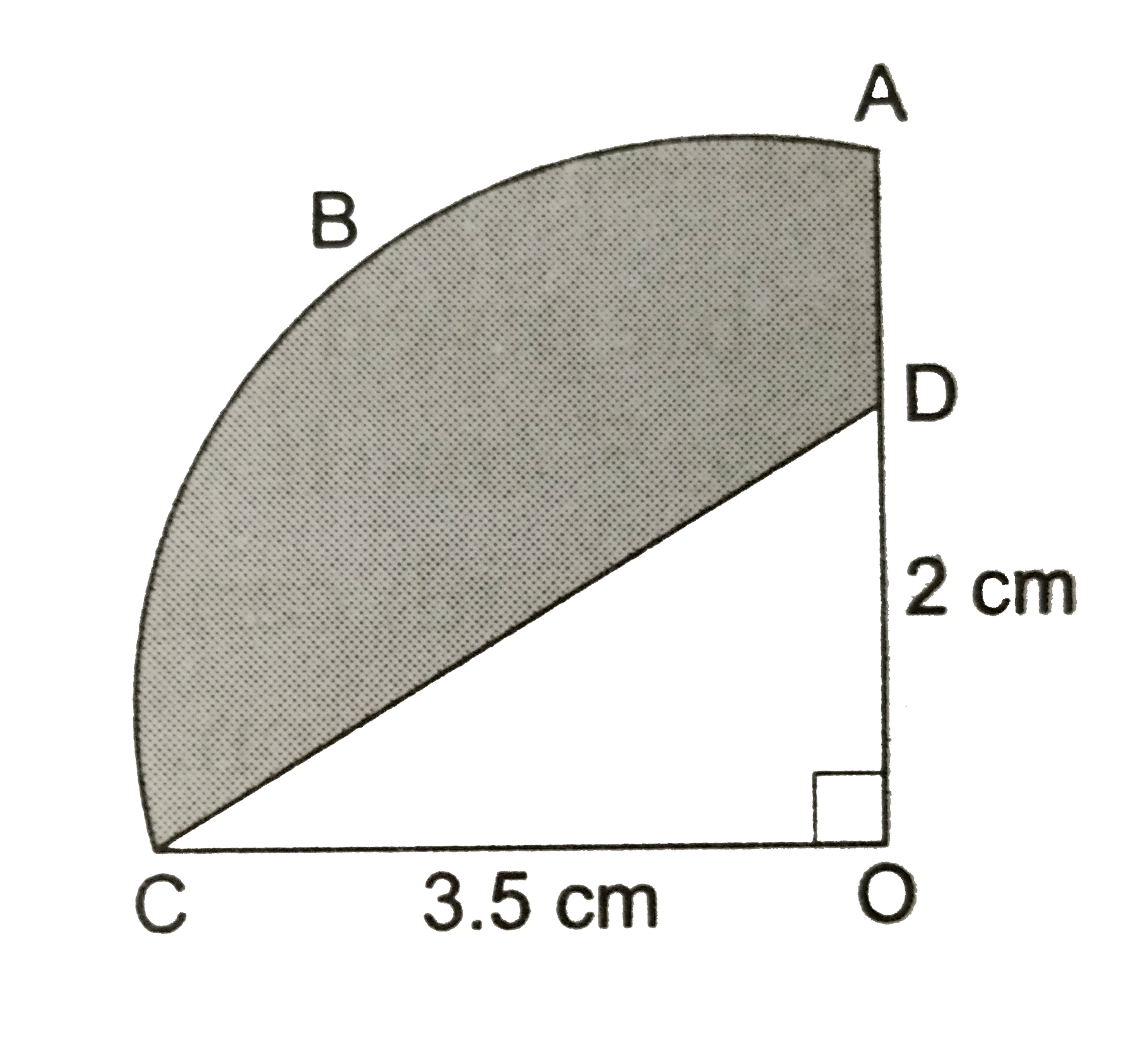
View SolutionIn the given figure OABC is a quadrant of a circle with centre O and radius 3.5cm.If OD=2cm,find the area of the shaded region.
View SolutionIn the figure, ACDB is a chord cutting two concentric circles with centre O. Find AB if CD = 8 cm, OD = 5 cm, and OB = 9 cm.
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View Solution

