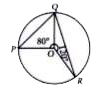
In the given figure, O is the centre of a circle in which ∠OAB=20∘ and ∠OCB=50∘ . Then . ∠AOC=?
A
50∘
B
70∘
C
20∘
D
60∘
Video Solution
Text Solution
The correct Answer is:D
OA=OB⇒∠OBA=∠OAB=20∘
ln ΔABC,∠CEB+∠OBA+∠AOB=180∘
⇒20∘+20∘+∠AOB=180∘⇒∠AOB=140∘
ln ΔOCB,∠OCB+∠OBC+∠COB=180∘
⇒50∘+50∘+∠COB=180∘⇒∠COB=80∘
∠AOB=40∘⇒∠AOC+∠COB=140∘
⇒∠AOC+80∘=140∘⇒∠AOC=60∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
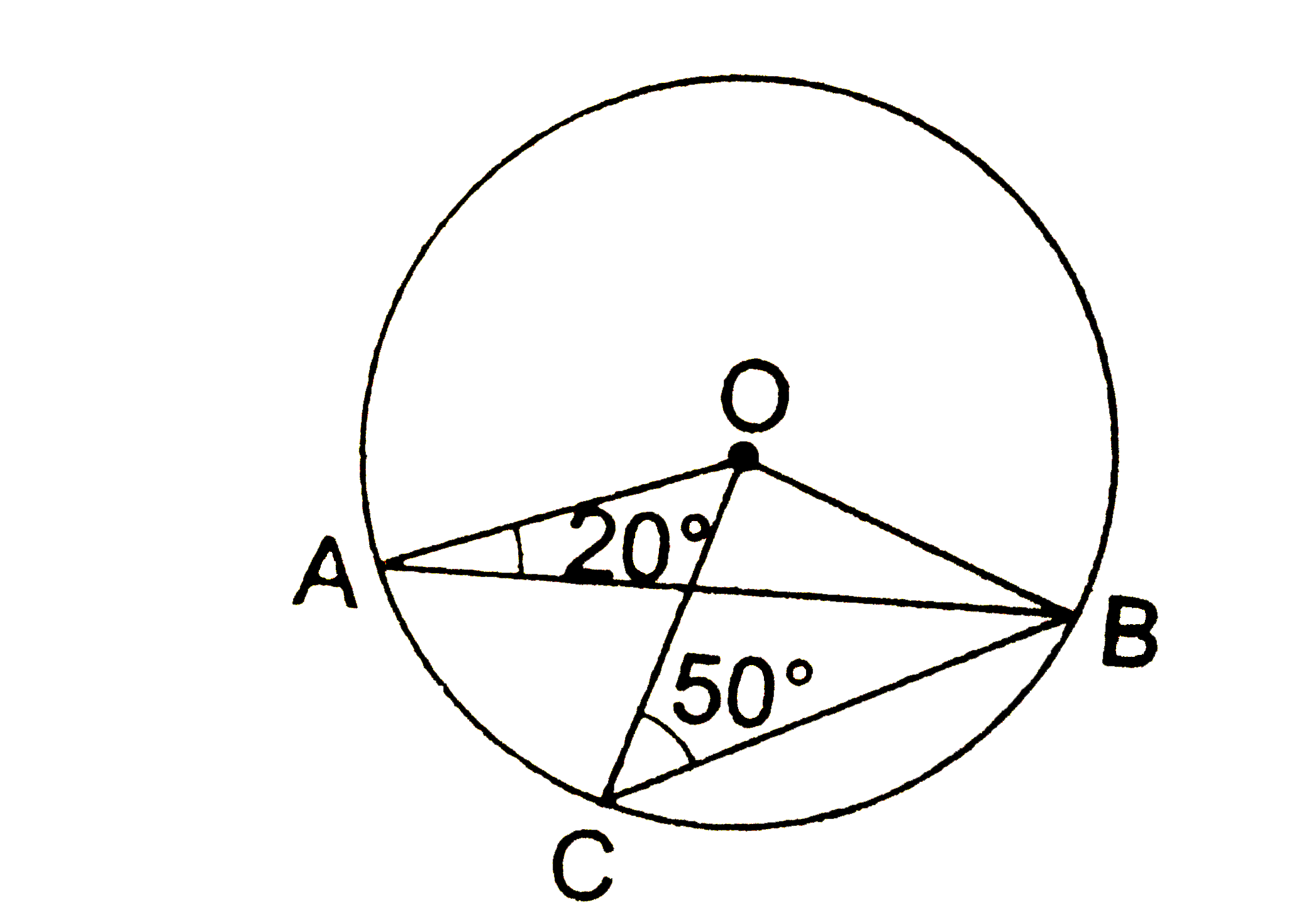
In the given figure, , O is the centre of a circle and ∠AOB=140∘. Then , ∠ACB=?
 A70∘B80∘C110∘D40∘
A70∘B80∘C110∘D40∘In the given figure, O is the centre of the circle. The value of x is
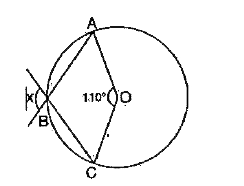 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘In the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
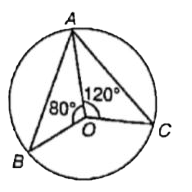 A120∘B80∘C100∘Dnone of the above
A120∘B80∘C100∘Dnone of the above
In the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
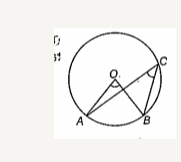
View SolutionIn the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB

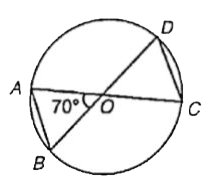
View SolutionIn the given figure, O is the centre of the circle. ∠AOB=70∘, find ∠OCD :
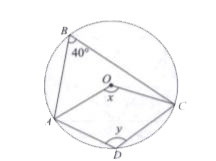
View SolutionIn the given figures, value of y (O is the centre of the circle) is
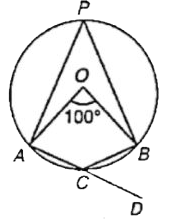
View SolutionIn the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
View Solution