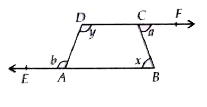
In the given figure, sides AB and AD of quad. ABCD are produced to E and F respectively. If ∠CBE=100∘ then ∠CDF=?
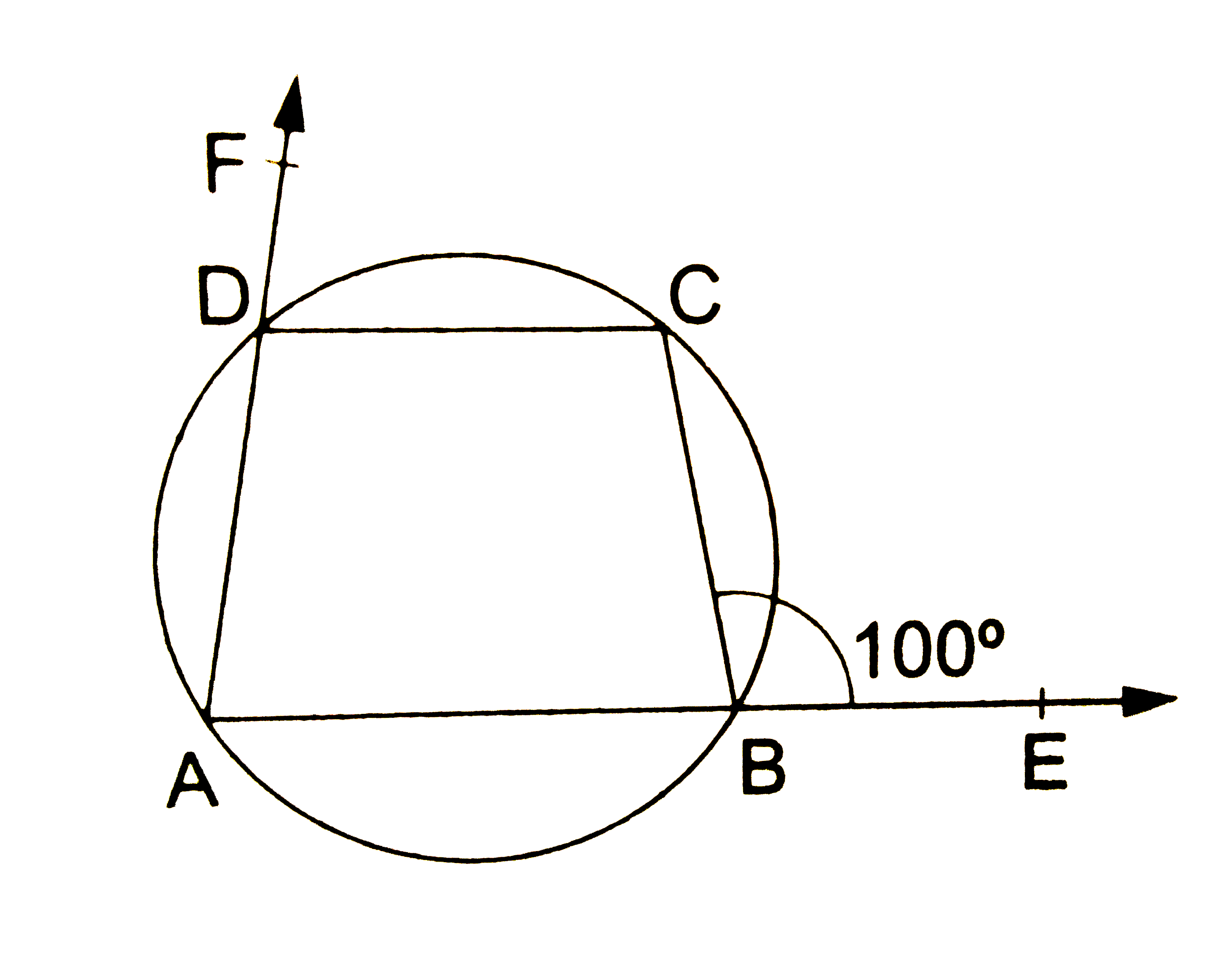
100∘
80∘
130∘
90∘
The correct Answer is:B
In cyclic quad. ABCD, int. opp. ∠ADC= ext. ∠CBE=100∘
∴∠CDF=180∘−∠ADC=180∘−100∘=80∘
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
ABC is a triangle and the sides AB, BC and CA are produced to E, F and G respectively. If ∠CBE=∠ACF=130∘ then the value of ∠GAB is
A100∘B130∘C80∘D90∘In the figure , if AD, AE and BC are tangent to the circle at D,E and F , respectively , then
 AAD=AB+BC+CAB2AD=AB+BC+CACAD2=AB+BC+CADAD4=AB+BC+CA
AAD=AB+BC+CAB2AD=AB+BC+CACAD2=AB+BC+CADAD4=AB+BC+CAIf the sides BA and DC of quadrilateral ABCD are produced as shown in the given figure, then
 Ax+y=a+bBx−y=a−bCx−y2=a−bD2(x+y)=a+b
Ax+y=a+bBx−y=a−bCx−y2=a−bD2(x+y)=a+b
In triangle ABC, AD and aEarn ABCD is a rhombus, AB is produced In the figure bisector of B and D of quadrilateral ABCD meet CO and AB produced and Q respectively. Prove that angle P t angle Q (angle ABC t le ADC). A
View SolutionIn the given figure, ABCD is a quadrilateral and E and F are points on AD and CD respectively such that AB = CB, ∠ABE=∠CBFand∠EBD=∠FBD. Prove that BE=BF.
View SolutionIn the given figure ABCD is a parallelogram in which AB||CD and E and F are the mid points of AB and BC respectively. What is the area of ∠BEF?
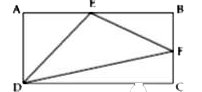
View SolutionIn the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar(△ADF)=ar(△DCE).
View SolutionABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
View Solution