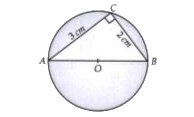
In the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
To solve the problem, we need to show that CA=2⋅OD given that OD is perpendicular to the chord AB and BC is a diameter of the circle.
1. Understand the Given Information:
- Let O be the center of the circle.
- OD is perpendicular to the chord AB.
- BC is a diameter of the circle.
2. Use the Property of Perpendicular from the Center:
- Since OD is perpendicular to AB, it bisects the chord AB. Therefore, we can write:
AD=DB
- Let AD=DB=x. Thus, the length of the chord AB can be expressed as:
AB=AD+DB=x+x=2x
3. Identify the Radius:
- Since BC is a diameter, OB and OC are both radii of the circle. Therefore:
OB=OC=r
- The radius r can also be expressed in terms of OD using the right triangle ODB:
OB2=OD2+DB2
- Substituting DB=x:
r2=OD2+x2
4. Use Triangle Similarity:
- Consider the triangles ODB and CAB. Since OD is perpendicular to AB and BC is a diameter, triangles ODB and CAB are similar by AA (Angle-Angle) similarity criterion.
- The ratio of the sides of similar triangles gives us:
ODCA=DBAB
5. Substitute Known Values:
- We know AB=2x and DB=x:
ODCA=x2x=12
6. Cross-Multiply to Find CA:
- From the ratio, we can cross-multiply:
2⋅OD=CA
- Thus, we have shown that:
CA=2⋅OD
Conclusion:
We have proved that CA=2⋅OD.
- Let O be the center of the circle.
- OD is perpendicular to the chord AB.
- BC is a diameter of the circle.
- Since OD is perpendicular to AB, it bisects the chord AB. Therefore, we can write:
AD=DB
- Let AD=DB=x. Thus, the length of the chord AB can be expressed as:
AB=AD+DB=x+x=2x
- Since BC is a diameter, OB and OC are both radii of the circle. Therefore:
OB=OC=r
- The radius r can also be expressed in terms of OD using the right triangle ODB:
OB2=OD2+DB2
- Substituting DB=x:
r2=OD2+x2
- Consider the triangles ODB and CAB. Since OD is perpendicular to AB and BC is a diameter, triangles ODB and CAB are similar by AA (Angle-Angle) similarity criterion.
- The ratio of the sides of similar triangles gives us:
ODCA=DBAB
- We know AB=2x and DB=x:
ODCA=x2x=12
- From the ratio, we can cross-multiply:
2⋅OD=CA
- Thus, we have shown that:
CA=2⋅OD
We have proved that CA=2⋅OD.
Topper's Solved these Questions
Similar Questions
In the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD
View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn a circle OD is perpendicular to chord AB of a circle with centre O. If BC is a diameter then the AC/OD is:
View SolutionIn Figure, OA and OB ar respectively perpendiculars to chords CD and EF of a circle whose centre is O. If OA=OB , prove that CE=DF.

View SolutionIn the given figure, O is the centre of the circle.

Name all chords of the circle.
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionIn the given figure, AOB is a diameter of a circle with centre O. Find tan A tan B.
View SolutionIn given figure, O is the centre of the circle.
A chord, which is not the diameter of the circle is
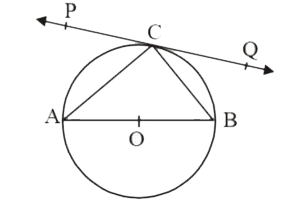
View SolutionIn figure PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB=30∘, find ∠PCA
View Solution

